【python】Lasso(ラッソ)回帰で疎なデータに対応しよう|機械学習
こんにちは、青の統計学です。
今回は、スパース学習の代表例である、Lasso(回帰)について解説いたします。
正則化項にL2ノルムを使う、リッジ回帰については、以下のコンテンツをご覧ください。
【python】Ridge(リッジ)回帰で多重共線性を解決する話
ラッソ回帰(Lasso regression)
スパース学習(sparce)とは
スパース学習とは、データのうち限られたデータだけが有益とされるデータで学習を行うことです。
いらない特徴量が多いというわけです。
例えば、顔を認証する画像解析ならば、「背景」という情報は機械学習によっては不要です。
ただ、事前に「この特徴量はいらない」と判断できれば良いのですが、
・事前にはわからない
・わかったとしても数が多すぎて処理できない
・人間主導で取捨選択を行うのは再現性に欠ける
などの理由で、前処理的に非ゼロの特徴量を抽出することはあまり推奨されていません。
今回は、そんなスパース学習の代表例としてラッソ回帰をご紹介します。
分類に使われる、スパースロジスティック回帰は扱いませんのでご注意ください。
正則化と正則化項について(regularization)
さて、ラッソ回帰は重回帰モデルの各回帰係数の算出時に正則化項というペナルティを設けています。
ラッソ回帰における正則化項をL1ノルムと呼びます。
通常の重回帰分析では、予測値と実測値の差を表す損失関数(平均二乗誤差など)が最小になる各回帰係数の組み合わせを求めます。
しかし、ラッソ回帰では、損失関数と正則化項の和が最小となる各回帰係数の組み合わせを求めるようにします。
L1ノルムは以下のように表します。
$$(\sum_{i=1}^{N}|β_{i}|)$$
L1ノルムとは、各回帰係数の2乗の和であることがわかりました。
最小二乗法にL1ノルムという制約を加えた最適化問題を考えます。
$$\sum_{I}(Y_{I}-f(X_{I}))^2$$
$$subject \quad to \sum_{l=1}^{L}|β_{I}|≦A$$
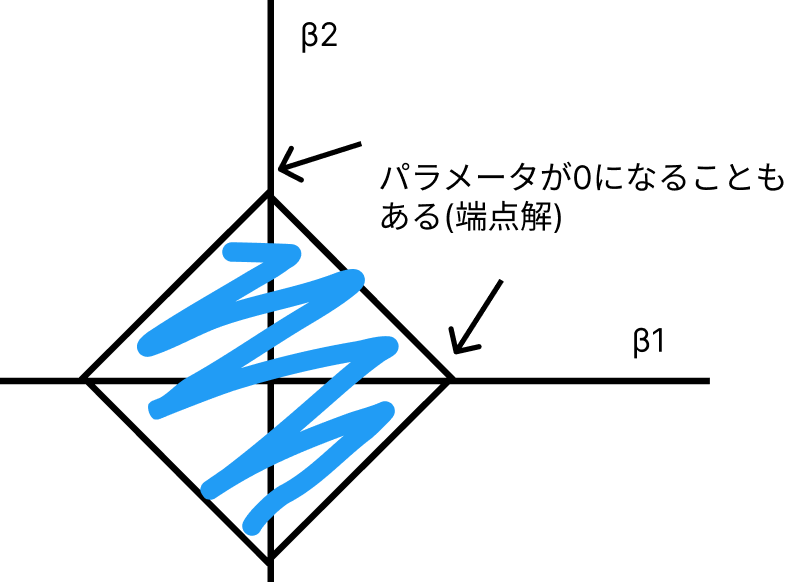
高校数学の知識を使えば、この制約が菱形の形をとるということに気づくと思います。
\(\sqrt{A}\)は円の半径ですね。\(A=0\)だと推定量はサンプル平均と一致し、\(A=∞\)だと最小二乗推定量に一致します。
補足:最小二乗法(ols)とは
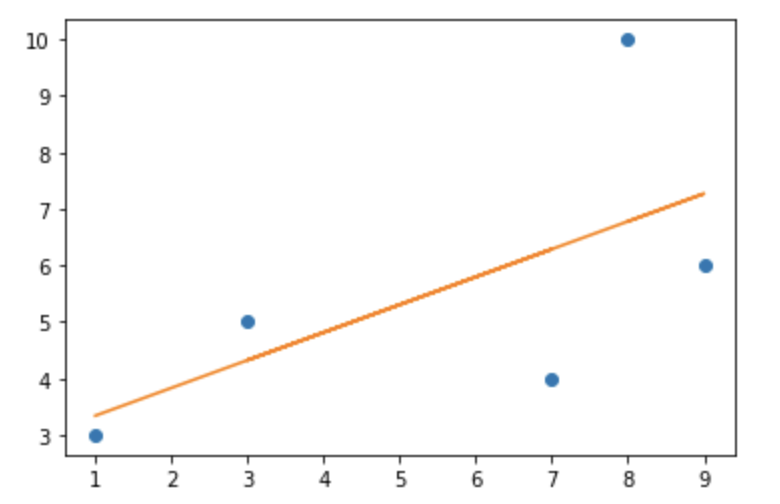
さて、最小二乗法とは最も知られている線形回帰の手法の一つです。
基本的には、予測値と実際の数値の差ができるだけ小さくなるような予測曲線をとるために学習を行います。
つまり、損失関数には平均二乗誤差(MSE)を取るということですね。
【MSEを最小化】ガウス・マルコフの定理と最良線形不偏推定量について
import numpy as np
import matplotlib.pyplot as plt
def least_squares_fit(x, y):
x_mean = np.mean(x)
y_mean = np.mean(y)
numerator = np.sum((x - x_mean) * (y - y_mean))
denominator = np.sum((x - x_mean) ** 2)
m = numerator / denominator
b = y_mean - m * x_mean
return m, b
x = np.array([1, 7, 3, 9, 8])
y = np.array([3, 4, 5, 6, 10])
m, b = least_squares_fit(x, y)
plt.plot(x, y, 'o')
plt.plot(x, m * x + b)
plt.show()
説明変数のベクトルがはる超平面に目的変数を直行射影したものと線形代数では言えますね。
ちなみに\(R^n\) において次元がちょうど 1 だけ小さい \(n − 1\) 次元 の空間のことを超平面 (hyperplane) といいます。
さて、話はラッソ回帰に戻ります。
ラグランジュ未定乗数法を使って制約式を書き換えると以下のようになります。L2正則化項は第2項にあたります。
$$(y-β_{0}+β_{1}X_{1}+…+β_{n}X_{n})^2+α(\sum_{i=1}^N|β_{i}|)$$
そして、図示すると以下のようになります。
縦軸は損失、横軸はパラメータを表しております。
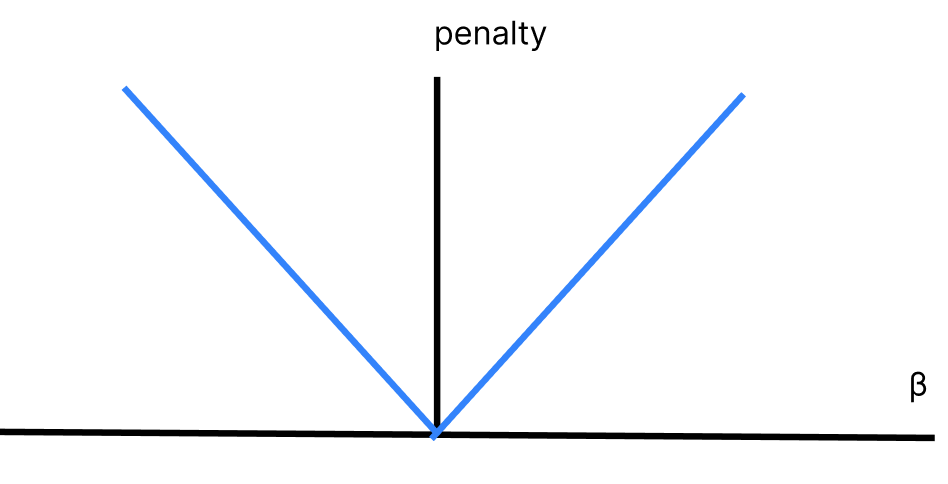
リッジ回帰の場合とは違い、V字の線を描くため\(β=0\)の近傍でも限界罰則は同じです。
正則化項を使う回帰の手法として、ラッソ回帰とは別にリッジ回帰(正則化項はL2ノルムと呼ぶ)があります。
以下のような違いがあります。
ラッソ(Lasso)回帰:各説明変数の回帰係数を0に近づけつつ、特定の説明変数の回帰係数を0にするという特性
リッジ(Ridge)回帰:各説明変数の回帰係数を0に近づけるが、完全には0にしない。どの特徴量も大事なときに有効。
ラッソ回帰は次元削除に似た考えですね。
こうした正則化は、回帰係数が大きくなることで発生する過学習を防ぐ上でも有効です。
またラッソ回帰に関しては、説明変数が一つ減るので解釈のしやすさが高まります。
正則化パラメーターの調整で、回帰係数にどんな変化が起きるのか
さて、正則化パラメーターαは基本的に0から1までの値で調整し、値が大きいほどペナルティが大きく、推定される回帰係数の値が小さくなります。
An Introduction to Statistical Learningでは、正則化パラメータの調整に関して以下のように解説しています。
正則化パラメータが0に近ければ近いほど、分散は大きくなり、バイアスは小さくなる。
→つまり、正則化の効果が薄い状態
正則化パラメータが大きいほど、分散は小さくなり、バイアスは大きくなる。
一般的に、正則化パラメータの上昇による分散の減少量は小さく、回帰係数の縮小により、回帰係数が過小評価され、バイアスの上昇幅としては大きくなります。
このような考えに基づくと、正則化を用いると比較的バイアスの上昇を最小限に抑えつつ、分散を大きく減らすことができる、データ数nに対して特徴量数pが大きい場合などに有用なことがわかります。
CODE
さて、Lasso回帰の特徴がわかったところでpythonで実演していきます。
今回使うデータはscikitlearnの糖尿病データセット(回帰)です。
BMIなどの個人の特徴量が並んでいて、そこからtagetとなる糖尿病の進行具合を以下に予測するかが肝です。
from sklearn.model_selection import train_test_split,cross_val_score
from sklearn.datasets import load_diabetes
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Lasso
from sklearn.metrics import roc_curve, auc
from sklearn.metrics import mean_squared_error
diabetes = load_diabetes()
seed =42
def get_eval_score(y_true,y_pred):
from sklearn.metrics import mean_absolute_error,mean_squared_error,r2_score
mae = mean_absolute_error(y_true,y_pred)
mse = mean_squared_error(y_true,y_pred)
rmse = np.sqrt(mse)
r2score = r2_score(y_true,y_pred)
print(f" MAE(平均絶対誤差) = {mae}")
print(f" MSE(平均二乗誤差) = {mse}")
print(f" RMSE(平均平方二乗誤差) = {rmse}")
print(f" R2Score(決定係数) = {r2score}")
def robust_z(x):
from sklearn.preprocessing import robust_scale
from scipy.stats import norm
coefficient = norm.ppf(0.75)-norm.ppf(0.25)
robust_z_score = robust_scale(x)*coefficient
return robust_z_score今回使うライブラリのインポートと関数の呼び出しを行います。
def robust_z(x)は、正規化用の関数です。ロバストZスコアという値を使っていて、外れ値に対して頑健な正規化を行います。
def get_eval_score(y_true,y_pred):は、予測結果の評価用の関数です。
決定係数を含め、4つの指標を用意しています。
# Pandasによるデータの表示
df_target = pd.DataFrame(diabetes["target"], columns=["target"])
df_data = pd.DataFrame(diabetes["data"], columns=diabetes["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
df.head()さて、ロードしたデータをデータフレーム型にしてみてみましょう。
df.head()で先頭の5行を出力することができます。
| target | age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
| 0 | 151.0 | 0.038076 | 0.050680 | 0.061696 | 0.021872 | -0.044223 | -0.034821 | -0.043401 | -0.002592 | 0.019908 | -0.017646 |
| 1 | 75.0 | -0.001882 | -0.044642 | -0.051474 | -0.026328 | -0.008449 | -0.019163 | 0.074412 | -0.039493 | -0.068330 | -0.092204 |
| 2 | 141.0 | 0.085299 | 0.050680 | 0.044451 | -0.005671 | -0.045599 | -0.034194 | -0.032356 | -0.002592 | 0.002864 | -0.025930 |
| 3 | 206.0 | -0.089063 | -0.044642 | -0.011595 | -0.036656 | 0.012191 | 0.024991 | -0.036038 | 0.034309 | 0.022692 | -0.009362 |
| 4 | 135.0 | 0.005383 | -0.044642 | -0.036385 | 0.021872 | 0.003935 | 0.015596 | 0.008142 | -0.002592 | -0.031991 | -0.046641 |
y = df["target"]
X = df.loc[:, "age":]
# 次数2で多次元交差項をつくる
polynomial_converter = PolynomialFeatures(degree=2,include_bias=False)
poly_features = polynomial_converter.fit_transform(X)
# 訓練データとテストデータにわける
X_train, X_test, y_train, y_test = train_test_split(poly_features, y, test_size=0.1, random_state=seed)
#スケーリングの作業
X_train_scaled = robust_z(X_train)
X_test_scaled = robust_z(X_test)
# 訓練データにモデルを適用(fit)する
model = Lasso(fit_intercept=True)
model.fit(X_train_scaled,y_train)
# 訓練データとテストデータを予測する
train_pred = model.predict(X_train_scaled)
test_pred = model.predict(X_test_scaled)ここが一番大事な部分です。
・まずyに目的変数、Xに説明変数を代入します。
・次に、あえてデータをスパースにします。
具体的には、交互作用項という、説明変数同士の積の値となる特徴量を複数作り、次元を増やします。
(事前に何が必要で、何がいらないかわからないからです。)
$$Y_{i}=β_{0}+β_{1}X_{1}+β_{2}X_{2}+β_{3}X_{1}X_{2}+β_{4}X_{1}^2+β_{5}X_{2}^2$$
\(X_{1}X_{2}\)のように、説明変数同士の席で表される項を交互作用項と呼びます。
2次以降の説明変数の線形で表される回帰を、多項式回帰と呼びます。
PolynomialFeatures()というメソッドを使えば、すぐに実現可能です。
degreeの値で何次の項まで作るか決定しますが、基本4以上は使いません。
・次に事前に定義しておいたロバストZ関数を使って、特徴量を全て正規化します。
線形回帰にはスケーリングの作業が大事ですので忘れずに行いましょう。
・あとは、機械学習のお決まりでfit→predictの流れです。
print("教師データ")
get_eval_score(y_train,train_pred)
print("テストデータ")
get_eval_score(y_test,test_pred)教師データ MAE(平均絶対誤差) = 41.03511166409648 MSE(平均二乗誤差) = 2574.370307377159 RMSE(平均平方二乗誤差) = 50.73825290032323 R2Score(決定係数) = 0.5642966335753805 テストデータ MAE(平均絶対誤差) = 41.40254486733264 MSE(平均二乗誤差) = 2706.93970516491 RMSE(平均平方二乗誤差) = 52.028258717401926 R2Score(決定係数) = 0.5574642698768644
冒頭でdef get_eval_scoreで定義した、Lasso回帰で推測された値を評価します。
教師データを入力して予測したデータと、テストデータを入力して予測したデータの2つを使いました。
教師データとテストデータともに、決定係数は0.6に届かない程度です。
過学習はしていないようですが、当てはまりとしては、それほど良くはないですね。
score = cross_val_score(model, X_train_scaled, y_train, cv=10)
print("交差検証の結果")
print(score)
print("交差検証の平均")
print("{:.4f}".format(np.mean(score)))交差検証の結果 [0.34489116 0.51737205 0.4223235 0.49584159 0.18438674 0.47910072 0.61980927 0.56274432 0.32382961 0.39035964] 交差検証の平均 0.4341
交差検証法(クロスバリデーション)を使って、平均値をとります。
目的としては、偏ったデータセットに分割してしまったせいで、精度がぶれてしまうことによる評価の間違えを防ぐためです。
cross_val_scoreというメソッドのcvという引数に、分割回数を設定し、10回分割しました。
ラッソ回帰は多重共線性にも対処できる
共線性のある特徴量を消してくれるという観点から、ラッソ回帰は多重共線性への対処法の一つとして挙げられます。
多重共線性とは、説明変数同士が強く相関しているという状態で、主に線形回帰の場合に問題になります。
数式的な定義としては、以下になります。
全てのa_iが0である場合を除いて、以下の事柄が成り立つ場合には多重共線性があると認められます。
$$a_0+a1X_{1i}+a_2X_{2i}+…+a_kX_{ki}≠0$$
方程式を満たす組み合わせがないということです。
多重共線性の識別方法など、詳細については以下のコンテンツをご覧ください。
【論文解説】多重共線性は回帰分析にどのような影響を与えるのか
Lasso回帰が良いのか、Ridge回帰が良いのか
前述した通り、ラッソ回帰ではパラメータを0する機能があります。
つまり、疎なデータ(sparce)では無駄な特徴量を省くことができます。
一方でリッジ回帰では、パラメータが0になることはなく、疎なデータでは無駄なデータを省けないと一般には言われています。
つまり、背景知識をもとに特徴量を選択したような密なデータ(dence)では、リッジ回帰の方が良いと考えられます。
遺伝子系や画像などの、スパースデータに関してはLasso回帰でいらない特徴量を減らした方が良いと考えられています。
画像などは特に、「この画像に写っているのは猫かどうか」を確かめるときに、背景の家などをうつした特徴量はいらないですね。
余談ですが、「この画像に映る動物は犬か猫か」という判定問題に対して、機械学習では背景が重要だと判断された話はあります。
例えば、犬を写した背景なら散歩中の草むらや屋外を写しがちですが、猫の写真の背景は基本的に家や布団、床などの屋内ですよね。
2乗項や交差項を大量に作成した場合も、ラッソが適しているかもしれません。
エラスティックネット(elastic net)とは
ラッソ回帰とリッジ回帰をバランスさせた損失関数を作る方法もあります。
これをエラスティックネットと呼びます。
以下のような損失関数を持ちます。
\(\sum_{I}(Y_{I}-f(X_{i}))^2+λ{\sum_{l}[α|β_{1}|+{\frac{1}{2}}(1-α)β_{l}^2]}\)
パラメータに絶対値をつけたラッソ回帰のペナルティとパラメータを二乗したリッジ回帰のパラメータがありますね。
他の教師あり学習モデルについては、以下をご覧ください。
【XGB】交差検証法を使った勾配ブースティング決定木の実装|python
【python】Ridge(リッジ)回帰で多重共線性を解決する話
【ランダムフォレスト】ブートストラップ法を決定木に応用|python
【判別問題】サポートベクトルマシン(SVM)の仕組み|python
【kaggle】ベイズ最適化とXGBでtitanicの予測問題を解く|python
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


