ロジスティック分布とは?シグモイド関数との関わりも解説
1. ロジスティック分布の定義と基本性質
「ロジスティック回帰」「シグモイド関数」といったキーワードを聞くと、0 から 1 までの連続値を確率のように扱うイメージを持つ方が多いかもしれません。
たとえば「あるメールがスパムである確率」「ある日、雨が降る確率」「サッカーの試合で特定チームが勝つ確率」など、いずれも 0~1 の範囲で表したいですよね。実はこのような「二値(YES/NO)を扱いたい」「確率の形で表したい」という要求の背景にあるのが、ロジスティック分布という確率分布です。
1.1 標準ロジスティック分布
まずロジスティック分布 (logistic distribution) を定義します。
標準ロジスティック分布 とは、位置パラメータ(location parameter)を ${\mu = 0}$、スケールパラメータ(scale parameter)を ${s = 1}$としたときの確率分布のことを指します。
- 累積分布関数 (CDF) はシグモイド関数そのものであり、以下のように定義されます。
$${F(x) \;=\; P(X \le x) \;=\; \frac{1}{1 + e^{-x}}}$$
- 確率密度関数 (PDF) は CDF を微分することで求められ、次の式で与えられます。
$${f(x) \;=\; F'(x) \;=\; \frac{d}{dx}\Bigl(\frac{1}{1 + e^{-x}}\Bigr) \;=\; \frac{e^{-x}}{(1 + e^{-x})^2}}$$
これがロジスティック分布のさまざまな応用の根拠となっていきます。
1.2 一般のロジスティック分布
より一般には、位置パラメータ ${\mu}$とスケールパラメータ ${s > 0}$を導入し、ランダム変数${X}$がロジスティック分布に従うことを次のように書きます。
$${X \sim \text{Logistic}(\mu, s)}$$
このとき、累積分布関数と確率密度関数はそれぞれ
$${F(x) \;=\; \frac{1}{1 + \exp\!\Bigl(-\frac{x – \mu}{s}\Bigr)}}$$
$${f(x) \;=\; \frac{\exp\!\Bigl(-\frac{x – \mu}{s}\Bigr)} {s \,\Bigl(1 + \exp\!\bigl(-\frac{x – \mu}{s}\bigr)\Bigr)^2}}$$
標準ロジスティック分布は ${\mu = 0,\, s = 1}$の特別な場合です。

ロジスティック分布が正規分布に比べて裾が重い 特性を持つ といった点は、後ほどロジスティック回帰の文脈でも影響を及ぼすので、覚えておいてください。
ロジスティック分布のパラメータを動かしながら分布の形を確認したい人は、以下の青の統計学 DS Playground 確率分布可視化ツールが便利です。
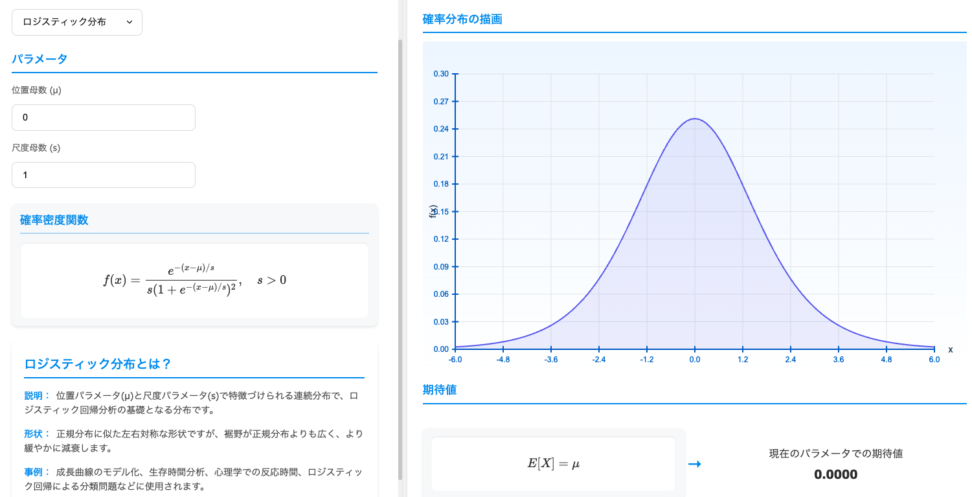
以下のリンクをクリックすると、ロジスティック分布のページに遷移します。
2. シグモイド関数との関係
ロジスティック分布の 累積分布関数はよく知られるシグモイド関数そのものです。
シグモイド関数と呼ばれる関数は、一般に「${(1 + e^{-x})^{-1}}$」という形状のものを指します。
- シグモイド関数は ${x \to \infty}$のときに ${1}$ に漸近し${x \to -\infty }$のときに${0}$に漸近する。
- 形状が “S” 字カーブになるため、連続的な 0 から 1 への遷移 をモデリングする際に有用。
このシグモイド関数によって、確率のような「0 から 1 の値の範囲しか持たない量」を数理的に扱うことが可能になります。
3. ロジスティック回帰との関連
3.1 ロジスティック回帰の基本的な考え方
ロジスティック回帰 (logistic regression) は、二値分類問題(例:あるメールがスパムかどうか、ある病気に罹患しているかどうかなど)を扱うために広く用いられる手法です。
従来の線形回帰では、予測対象が連続値であるため、予測値は理論上 ${-\infty}$から ${\infty}$まで取りうる値になります。しかし二値分類では、出力は「${0}$ or${1}$」の離散的なラベルになるため、これを直接線形回帰で扱うのは不自然です。
そこでロジスティック回帰では、線形結合
$${w_1 x_1 + w_2 x_2 + \cdots + b}$$
をいったん連続値として計算し、それをシグモイド関数で 0~1 の区間にマッピングします。
つまり
$${p = \frac{1}{1 + \exp\!(- (w_1 x_1 + w_2 x_2 + \cdots + b))}}$$
この${p}$が「クラス 1(ポジティブ)である確率」を表す推定値になるわけです。
3.2 ロジスティック分布を背後に持つ理由
「どうしてシグモイド関数なのか?」という問いに対しては、ロジスティック分布 を暗黙の誤差分布として仮定する二値応答モデルに由来するという説明がよくなされます。つまり、確率的線形モデルを想定し、その誤差がロジスティック分布に従うと考えると、自然にシグモイド関数が導かれるという理屈です。

もし誤差分布に正規分布を仮定すると、プロビット回帰(probit regression) という類似のモデルに行き着き、その場合のリンク関数は累積正規分布となります。
ロジスティック回帰では、このシグモイドの勾配 (導関数) が比較的単純である点が学習アルゴリズム上の利点となることも要因です。誤差逆伝播法や最急降下法などでパラメータを更新する際にもロジスティック関数は扱いやすい形状を持ちます。
まあReluが使われることの方が多く、シグモイド関数が使われるのは専ら出力層(ロジスティック回帰に相当する部分)であることが一般的ですね。
3.3 対数オッズとロジット関数
ロジスティック回帰やロジスティック分布の文脈では、しばしばlogit (ロジット) 関数という言葉が登場します。logit 関数は、シグモイド関数の逆関数であり、以下のように定義されます。
$${\text{logit}(p) \;=\; \log\!\Bigl(\frac{p}{1 – p}\Bigr)}$$
- ${p}$は${0}$から${1}$の範囲の値、すなわち確率を表す。
- ${\log\!\bigl(\frac{p}{1 – p}\bigr)}$は 対数オッズ (log odds)と呼ばれる量。
ロジスティック回帰では、
$${\text{logit}(p) \;=\; w_1 x_1 + w_2 x_2 + \cdots + b}$$
という形でモデル化し、${p}$はシグモイド関数で与えられるというわけです。
4. 正規分布との近さと差異
上でも少し図解として載せましたが、ロジスティック分布は、形状が「左右対称」「中央付近が膨らみ、裾が厚め」という点で正規分布にやや似ています。
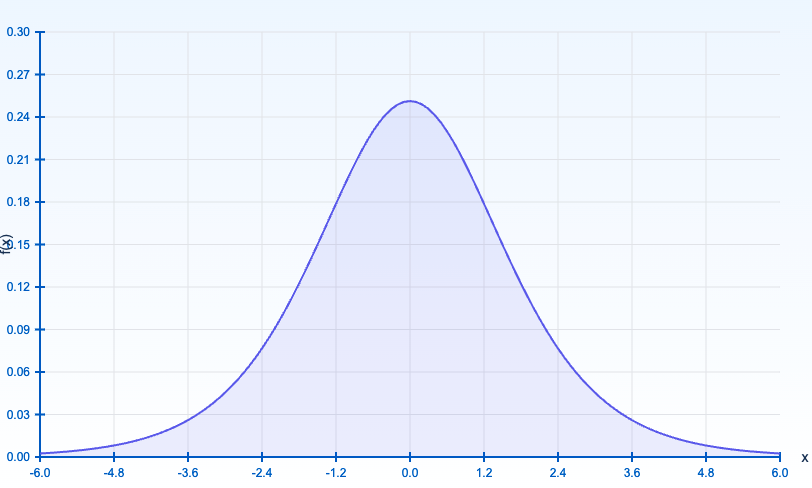
しかし裾の重さ (heavy tail) が正規分布よりも大きく、極値近くでの挙動が異なります。
具体的に言うと、ロジスティック分布は下記のように裾がゆっくりと減衰します。
$${\lim_{x \to \pm\infty} f(x) = \text{(ゆっくり減衰)}}$$
一方で正規分布は指数関数的に減衰するため、ロジスティック分布のほうが極端な値に対してもある程度の確率を割り当てることになります。
これは分類モデルの文脈では「外れ値の扱いやすさ」に関係することもあります。
5. おまけ|Item Response Theory (IRT) における二母数ロジスティックモデル
教育測定学や心理計量学の分野で使われる項目反応理論 (Item Response Theory: IRT) においては、二母数ロジスティックモデル (2PL model) や三母数ロジスティックモデル (3PL model) と呼ばれるものがあります。
これは、受検者の能力${\theta}$と問題(項目)の困難度、識別力などのパラメータを組み合わせ、回答確率をロジスティック関数で表すモデルです。
$${P(\text{正答} | \theta) \;=\; c + \frac{1 – c}{1 + \exp\{ -a(\theta – b) \} }}$$
- ${a}$は項目識別力パラメータ
- ${b}$は項目困難度パラメータ
- ${c}$は早期推測度(いわゆる「やまかん正答率」)パラメータ
教育測定の分野でも、ロジスティック分布由来のシグモイド関数をベースにすることで、「0~1 の範囲で確率を表す」という枠組みが自然に得られるわけです。
要は、受験者の能力を1問ごとにはかり動的に次の問題をかえ、適切に受験者の能力を測るというわけです。
日経の入社試験でよく導入されているSPAの問題設定もこの項目反応理論が応用されているようです。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!








