【判別問題】サポートベクトルマシン(SVM)の仕組み|python
今回は2値の判別問題で効果を発揮する、サポートベクトルマシン(support vector machine)について解説いたします。
数理最適化も扱うことになるのでいい勉強になると思います。
非線形分離に関しては以下のコンテンツをご覧ください。
【python】カーネルSVMとは?kernel関数を利用した非線形データの判別問題に挑戦|機械学習
サポートベクトルマシン(support vector machine)
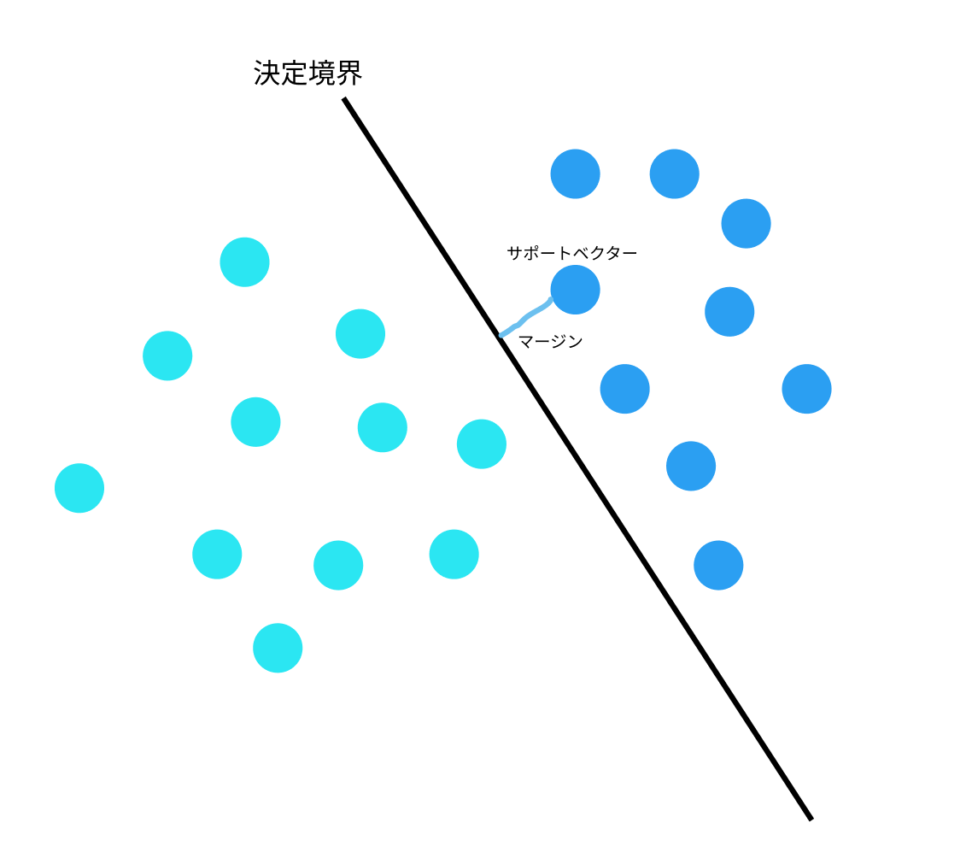
サポートベクトルとは、下図のような境界線(決定境界と言います)に最も近いデータのことです。
そしてサポートベクトルマシーンとは、サポートベクターと決定境界の距離(マージン)が最大になる決定境界を引くアルゴリズムです。
線形SVM
以下のような2値ラベル(+1,-1)がある状況を考えます。
$$(x_i,y_i),…,(x_n,y_n) {ただし}(x_i{\in{R^d},y_i{\in{(+1,-1)}}})$$
そして、上記のデータを以下のような線形判別器で学習することを考えます。
線形判別器は、決定境界を決める数式であると考えてください。
sign()は符号関数で、f(x)が0以上なら1を取り、0より小さければ-1を取ります。
$$F=(sign(f(x)|f(x))=w^Tx+b,w{\in{R^d},b{\in{R}}})$$
wとbはパラメータです。
データが線形分離可能な問題の場合、次の関係式が成り立ちます。
$$y_i=+1\Rightarrow W^Tx_i+b>0,-1\Rightarrow W^Tx_i+b<0$$
この二つに不等式は以下のように表すことができます。
これは、後に作る最適化問題の条件部分(守るべきルールのようなもの)です。
$$y_i(w^Tx_i+b)>0,(i=1,…n)$$
冒頭で申し上げた通り、SVMはマージンを最大化するアルゴリズムです。
正例と負例のデータの距離が最も大きくなるような決定境界を取りたいですね。つまり、数理最適化問題です。
$${\frac{w^Tx_i+b}{||w||}}$$
さて、x_iから判別平面X^Tx_i+b=0との距離は上のようになります。
ここだけなら、高校数学でもやりましたね。
つまり、線形SVMは以下のような数理最適化問題を解いているアルゴリズムだと言えます。
$$max_{w,b}\quad min_{i}{\frac{w^Tx_i+b}{||w||}},subject \quad to \quad y_i(w^Tx_i+b)>0$$
数式の訳としては以下になります。
min:あるxと判別平面との距離のうち最小のデータx_iを返す
max:返された最小の距離を最大化できるwとbを返す。
制約:線形分離可能なデータである。
線形のサポートベクトルマシンは、ロジスティック回帰と似たような結果になることが多いです。
ただ、ロジスティック回帰は確率に基づいたアルゴリズムですが、SVMは「マージンの最大化」を行うアルゴリズムです。
ロジスティック回帰については、以下をご覧ください。
非線形SVM
SVMのマージン最大化という定式化では、全ての学習データが線形分離可能であるという仮定を置いていました。
しかし、この仮定を緩和して線形分離でなくても定義できるソフトマージン最大化によって判別関数を求めることができます。

このような場合、損失関数を与え、損失関数が最小になるようなwとb(係数)を持つ決定境界が作成されます。
具体的には以下のルールです。
$$y_i(w^TX_i+b)>1{の時、損失は0}$$
積が1以上の時、十分に2値を分類できているとして損失を0とします。
$$y_i(w^TX_i+b)<1{の時、損失は{1-(w^TX_i+b)}}$$
積が1以下の時、十分に2値を分類できていないため、損失を出します。不等式から当然この値は0より大きいです。
つまり、先ほどの最適化の条件「積が0より大きい」を消して、以下の変数(スラック変数)を加えたものが、線形分離不可能な場合の線形判別器の関数です。
$$max \quad (1-y_i(w^TX_i+b),0)$$
ただ、下のような螺旋状のデータなどは線形判別器では処理することはできません。
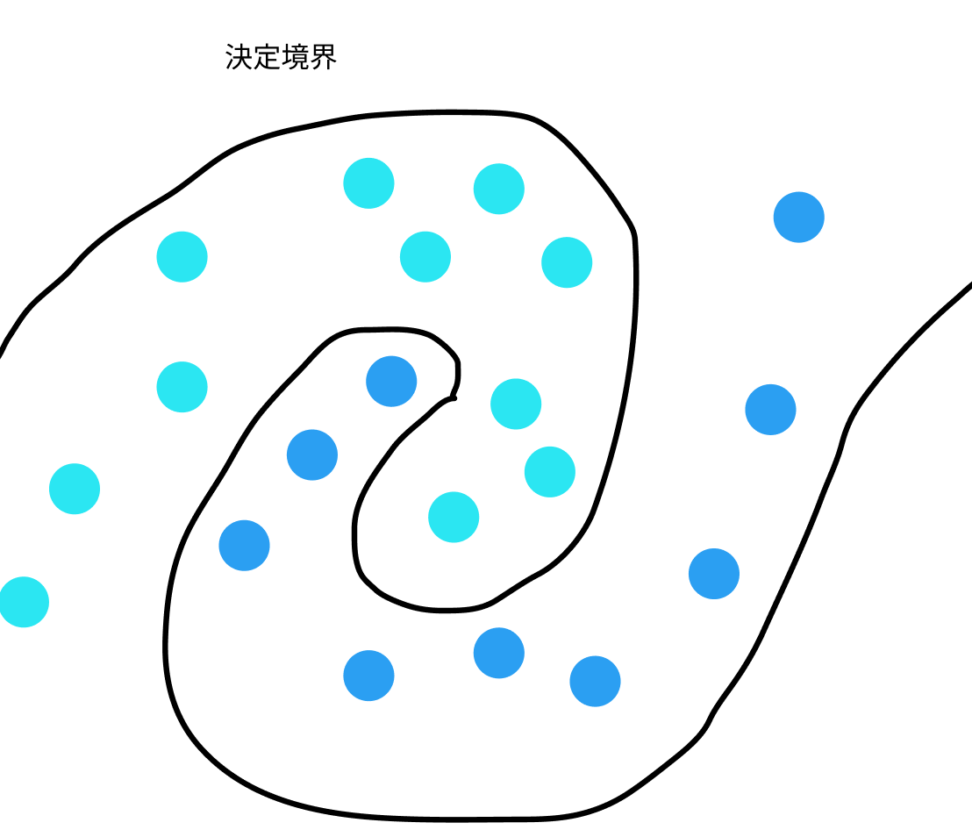
数式まで詳しく扱いませんが、カーネル関数という関数を使い、モデリングすることで表現力を上げて対応しています。
基本的に線形判別器と同じで、定式化して最適化問題を解くことで決定境界が求められます。
超平面(hyper plane)とサポートベクトルマシンの関係
これまでの図では、二次元平面上に決定境界を引く、つまり線を引くことで表現してきました。
一方で、現実のデータとしては高次元の場合も多く、境界が線であることは少ないです。
ここで決定境界の一般化として、「超平面」という概念をご紹介いたします。
超平面は、高次元空間での分離平面の一般化です。
\(R^n\) において次元がちょうど 1 だけ小さい \(n − 1\) 次元 の空間のことを超平面 (hyperplane) といいます。
例えば、2次元空間では、超平面は直線になります。3次元空間では、超平面は平面になります。より高次元の空間では、超平面はその空間を分割する n-1 次元の平面になります。
$$w^T * x + b = 0$$
w は n次元の重みベクトルです。x は n次元の入力データポイントです。b はスカラー値で、バイアス項と呼ばれます。
繰り返しますが、データと超平面の大小関係で分類するということですね。
SVMは、クラスを最もよく分離する超平面(決定境界)を見つけることを目指しています。
この超平面は、異なるクラスのデータ点との距離(マージン)が最大になるように選択されます。
統計検定のチートシートは以下をクリック!
【最短合格】統計検定準一級のチートシート|難易度や出題範囲について
【最短】統計検定2級合格ロードマップとチートシート|おすすめの本について
CODE
せっかくなので、カーネルソフトベクターマシンを使ってみます。
具体的な手順としては、
1:カーネル法によって線形サポートベクターマシンで決定境界をひく
2:元の状態に逆変換する
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
import numpy as np
import pandas as pd
data_breast_cancer = load_breast_cancer()
# Pandasによるデータの表示
df_target = pd.DataFrame(data_breast_cancer["target"], columns=["target"])
df_data = pd.DataFrame(data_breast_cancer["data"], columns=data_breast_cancer["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
df.head()乳がんデータを使います。
targetは目的変数で、0か1の2値分類問題です。
1:良性腫瘍
0:悪性腫瘍
target | mean radius | mean texture | mean perimeter | mean area | mean smoothness | mean compactness | mean concavity | mean concave points | mean symmetry | … | worst radius | worst texture | worst perimeter | worst area | worst smoothness | worst compactness | worst concavity | worst concave points | worst symmetry | worst fractal dimension | |
| target | 1.000000 | -0.730029 | -0.415185 | -0.742636 | -0.708984 | -0.358560 | -0.596534 | -0.696360 | -0.776614 | -0.330499 | … | -0.776454 | -0.456903 | -0.782914 | -0.733825 | -0.421465 | -0.590998 | -0.659610 | -0.793566 | -0.416294 | -0.323872 |
| mean radius | -0.730029 | 1.000000 | 0.323782 | 0.997855 | 0.987357 | 0.170581 | 0.506124 | 0.676764 | 0.822529 | 0.147741 | … | 0.969539 | 0.297008 | 0.965137 | 0.941082 | 0.119616 | 0.413463 | 0.526911 | 0.744214 | 0.163953 | 0.007066 |
| mean texture | -0.415185 | 0.323782 | 1.000000 | 0.329533 | 0.321086 | -0.023389 | 0.236702 | 0.302418 | 0.293464 | 0.071401 | … | 0.352573 | 0.912045 | 0.358040 | 0.343546 | 0.077503 | 0.277830 | 0.301025 | 0.295316 | 0.105008 | 0.119205 |
| mean perimeter | -0.742636 | 0.997855 | 0.329533 | 1.000000 | 0.986507 | 0.207278 | 0.556936 | 0.716136 | 0.850977 | 0.183027 | … | 0.969476 | 0.303038 | 0.970387 | 0.941550 | 0.150549 | 0.455774 | 0.563879 | 0.771241 | 0.189115 | 0.051019 |
| mean area | -0.708984 | 0.987357 | 0.321086 | 0.986507 | 1.000000 | 0.177028 | 0.498502 | 0.685983 | 0.823269 | 0.151293 | … | 0.962746 | 0.287489 | 0.959120 | 0.959213 | 0.123523 | 0.390410 | 0.512606 | 0.722017 | 0.143570 | 0.003738 |
目的変数と説明変数に分けます。
y = df["target"]
X = df.loc[:, "mean radius":]
#スケーリングの作業
#ロバストZスコアを採用
def robust_z(x):
from sklearn.preprocessing import robust_scale
from scipy.stats import norm
coefficient = norm.ppf(0.75)-norm.ppf(0.25)
robust_z_score = robust_scale(x)*coefficient
return robust_z_score
X_scaled = robust_z(X)次に説明変数を標準化します。
ロバストZスコアを使って、ハズレ値に強い標準化を行いました。
標準化した説明変数と目的変数を教師データと評価データに分割します。
# トレーニングデータとテストデータに分けて実行してみる
X_train, X_valid, y_train, y_valid = train_test_split(X_scaled,y, test_size=0.1, random_state=0)
from sklearn import svm
clf_result=svm.SVC(kernel='rbf',class_weight='balanced', random_state=0)
clf_result.fit(X_train, y_train)
#正答率を求める
pre=clf_result.predict(X_valid)
accuracy=metrics.accuracy_score(y_valid,pre)
print("正答率 = ",accuracy)次にインスタンスの生成です。
kernel=”rbf”は、Gaussian カーネルのことです。
γ値やコストパラメータのチューニングに関しては、今回は省略します。
→正答率 = 0.9824561403508771インスタンスを作ったのちに、fitしてpredictで完成です。
せっかくなのでaccuracyを求めてみました。
補足|線形判別分析とソフトマージンSVMはどう違うのか
分類タスクへの手法として線形判別分析(LDA)という手法があります。
こちらのコンテンツで数学的背景まで取り上げていますが、クラスター内の分散を最小化してクラスター間の分散を最大化するという最適化問題を解き、最適な判別平面を引きます。
今回取り上げたソフトマージン(幾らかの誤判別を許容してマージンを引く)SVMと違い、線形判別分析はそのような仮定を起きません。
その代わり、すべてのクラスが共通の共分散行列を持つという仮定を立てます。
この仮定により、LDAは非常に計算が効率的であり、多くの問題に対してうまく機能します。
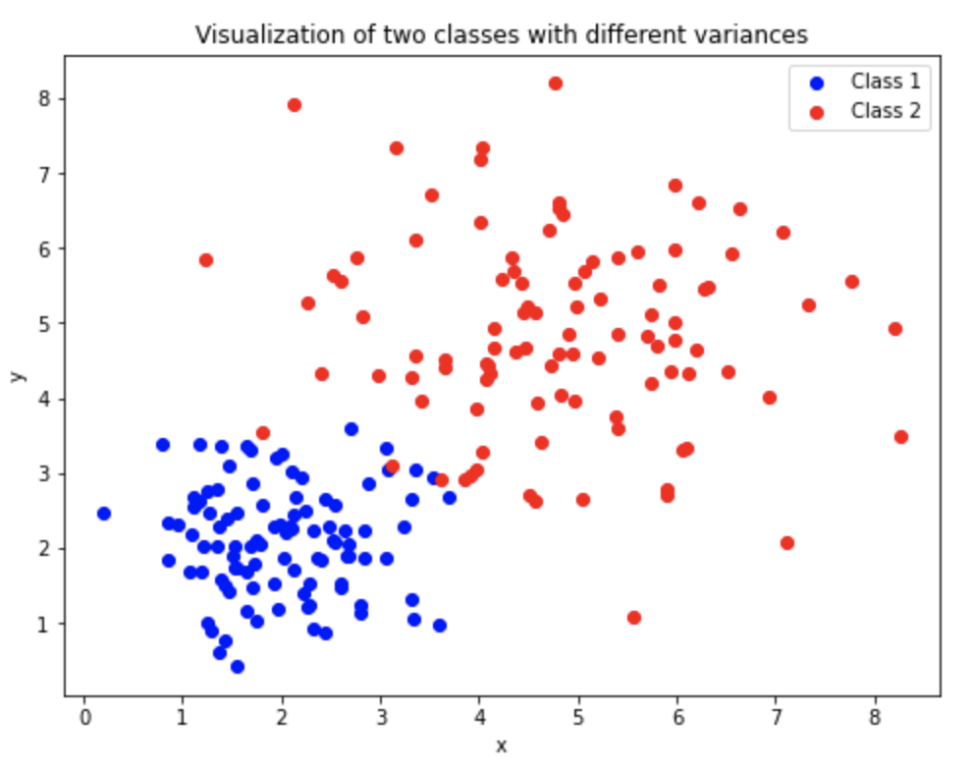
一方で、真のクラスター内の分散がそれぞれ大きく異なる場合には、分散が大きなクラスターの一部が分散が小さなクラスターに誤って分類されることになります。
つまり、結果として分類精度が低下する可能性があります。
そのため、各クラスのデータのバラつきが大きく異なる場合、特にデータが高次元である場合、ソフトマージンSVMがLDAよりも優れた結果を出す可能性があります。
他の機械学習コンテンツについては以下をご覧ください。
【Sequential】Kerasを使ったニューラルネットワーク|python
【XGB】交差検証法を使った勾配ブースティング決定木の実装|python
【ランダムフォレスト】ブートストラップ法を決定木に応用|python
【kaggle】ベイズ最適化とXGBでtitanicの予測問題を解く|python
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


