ロジスティック回帰についてわかりやすく解説【二項分布】【統計検定】
ロジット関数とロジスティック関数
こんにちは、青の統計学です、
今回は、分類タスクの王道「ロジスティック回帰」について解説していきます。
しっかり復習したい方は、以下の記事をご覧ください。
基本は、線形回帰の拡張でしたね。
具体的には、一般化線形モデル(Generalized Linear Models: GLMs)は、目的変数\(y\)と説明変数\(x\)の関係を線形のリンク関数\(g(.)\)を介して表現するモデルです。
そして、目的変数は正規分布以外にも従う可能性がある、と選択肢を広げているのがモチベーションの一つで、二項分布、ポアソン分布、ガンマ分布などの指数分布族に従うと仮定されます
ある分布に従う確率変数\(Y\)があるとして、その分布の平均を\(\mu\)とします。
\(\mu\)を変形した形f(\mu)にすると、目的変数を線形で表すことができます。
これを一般化線形モデル(GLM)と呼びます。
今回は、\(f(\mu)\)がロジットリンク関数であるものを扱います。
一般化線形モデルには、3つの特徴がありました。
$$f(\theta_{n})=\beta_{0}+\beta_{1}X_{1}+…+\beta_{k}X_{k}$$
①線形予測子:入力データ\(X\)の数だけ、パラメーターをかけたものです。
②確率分布:パラメーター\(\beta\)が得られた時の\(y\)の分布
③リンク関数:線形予測子が作る関数のことですね。\(Y\)が形を変えたものと考えてもらって構いません。
確率分布がポアソン分布の時のGLMは、リンク関数は\(\lambda\)を対数化したものになります。
下のような形でした。
$$log\lambda_{i}=\beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}$$
今回扱うロジスティック回帰の特徴
①確率分布：二項分布
②リンク関数：ロジットリンク関数
注意して欲しいのですが、カウントデータが１個のみなら①の確率分布はベルヌーイ分布になります。
ロジスティック関数(logistic function)
ロジット関数の逆関数が、ロジスティック関数です。
ロジスティック関数は以下のような形になります。
$$logistic(z_{i})=\frac{1}{1+exp(-z_{i})}$$
機械学習を勉強している方は、シグモイド関数といえばわかりやすいかと思います。
線形予測子\(z_i\)に\(-1\)がかかりました。
\(e\)の-線形予測子乗に1を足したものが分母となっています。
この関数は0から1の範囲の値をとり、\(z\)が大きくなると\(1\)に、小さくなると\(0\)に漸近します。
ロジスティック関数の役割は、説明変数\(x\)の線形結合\(Xβ\)を、確率\(\pi\)に変換することにあります。
つまり、実数値の線形予測子を、\(0\)と\(1\)の間の確率値に写像しています
ロジットリンク関数(logit link function)
ロジスティック回帰において、ロジットリンク関数(logit link function)は重要な役割を果たします。
ロジットリンク関数は、以下のように定義されます。
$$log \, \frac{q_{i}}{1-q_{i}}=z_{i}$$
右辺は線形予測子、左辺はオッズを対数化したものです。
コインの例で言うと、下のようになります。
$$log \frac{コインがi回表の確率}{コインがn-i回裏の確率}=z_{i}$$
ロジスティック回帰モデルは、この変換された線形予測子\( logit(q_i)\) を説明変数\(x\)の線形結合で表現します。
$$logit(q_i) = log(q_i / (1-q_i)) = \mathbf{X}\beta$$
つまり上のような形ですね！！
ロジットリンク関数を使うことで、\(0\)と\(1\)の間の値をとる確率\(\pi\)を、\(-\infty\)から\(\infty\)までの値をとる線形予測子\mathbf{X}\betaにリンクさせることができました。
オッズの解釈について
さて、ロジスティック回帰を扱う上でオッズの考え方は必ず押さえておきたいところです。
オッズとは、ある事象が起こる確率を起こらない確率で割ったものを指します。
確率\(\pi\)に対するオッズは、\(\frac{\pi}{(1-\pi)}と表されます。
例えば、\(\pi\)が\(0.8(80%)\)の時、オッズは\(0.8/0.2 = 4\)となります。
つまり、事象が起こる確率は起こらない確率の4倍であることを意味しています。
オッズの値域は\(0\)から\(\infty\)までで、\(0\)に近づくほど事象が起こりにくく、\(\infty\)に近づくほど起こりやすいことを示します。
上述した通り、ロジスティック回帰は、目的変数\(y\)が二項分布分布(0か1の二値)に従うと仮定し、\(y=1\)となる確率\(P(y=1|x)=\pi\)をモデル化します。
しつこいですが、この確率\(\pi\)と線形予測子\(\mathbf{X}\beta\)の関係は、ロジスティック関数を用いて以下のように表現されます。
＄$\pi = P(y=1|x) = 1 / (1 + exp(-(\mathbf{X}\beta)))$$
一方で、オッズを使えば別の表現もできます。
$$odds =\frac{ \pi}{(1-\pi)} = exp(\mathbf{X}\beta)$$
つまり、オッズは\(\mathbf{X}\beta\)の指数関数で表されます。
係数ベクトルβの値が増えるとオッズは exponential に大きくなり、\(y=1\)となる確率が高くなります。
このように、ロジスティック回帰ではオッズ、ロジスティック関数の概念を用いて、確率モデルと線形モデルをつなげることができました。
オッズとロジスティック関数の理解は、ロジスティック回帰の解釈や係数の意味付けに不可欠です。
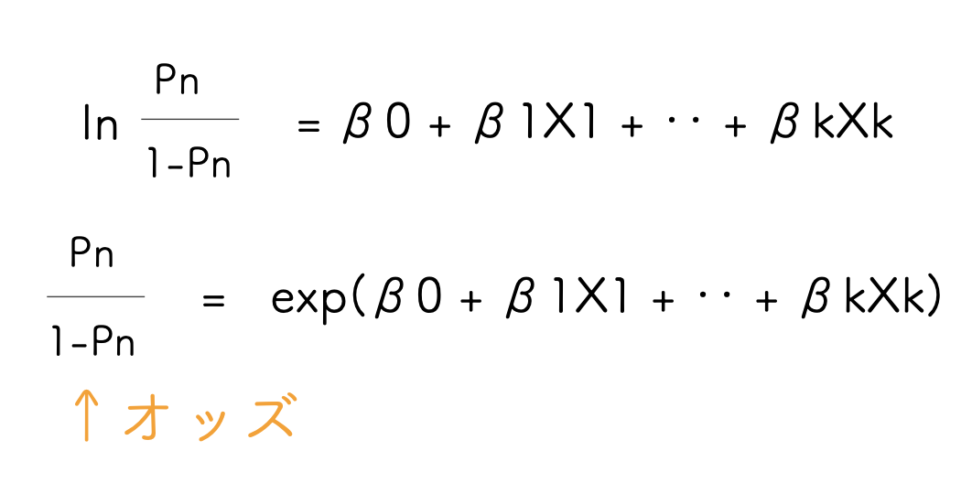
さて、対数オッズとオッズの話をします。
対数オッズと、オッズの関係は上のようになります。
上側の右辺がよくみる線形予測子の形です。
出力結果が、「オッズを対数化したもの」だと目的に沿わない場合もあります。
ちゃんと、「コインがi回表になる確率を知りたい！」と言う場合には、ロジット関数をロジスティック関数にする必要があります。
二項分布(binomial distribution)
ここでは、前提知識となる二項分布について補足をします。
二項分布とは、独立なベルヌーイ分布を\(n\)回繰り返した時の和の分布です。
実現値が有限である点において、ポアソン分布と異なります。
【例】コインを5回投げて表の出た回数をXとすると、実現値は0,1,2,3,4,5の6種類です。表が出る確率を仮にpとすると、実現値0と実現値1は以下のように表せます。
$$(1-p)^5$$
$$5p(1-p)^4$$
このようになっていきます。実現値0から5までの確率の和は以下のようになります。
$$p(x)={}_5C_xp^5(1-p)^{5-x}$$
一般化すると、二項分布の確率密度関数は以下のようになります。
nは実現値です。
$$p(x)={}_nC_xp^n(1-p)^{n-x}$$
補足：指数型分布族
リンク関数をロジット関数にすると、尤度関数が指数型分布族になるというメリットがあります。
以下のようなeの指数関数の形で確率密度を表せるものは、すべて指数型分布族と呼びます。
例えば、正規分布やガンマ分布、ポアソン分布などの主要な確率分布は全て指数型分布族です。
$$f(x;\theta)=ae^{\theta^TS(x)-ψ(\theta)}$$
例えば、\(N(\mu,1)\)を指数型分布族の形に直してみます。
$$f(x;\mu)=\frac{1}{\sqrt{2π}}e^{-\frac{(x-\mu)^2}{2}}=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}+\mu x-\frac{\mu^2}{2}}$$
ここでいう\(\theta\)とは、期待値\(\mu\)のことなので、以下のようになります。
\(a\)は\(x\)の関数です。
\(a\)と\(e\)の積では、指数同士を足し算しています。
$$a=\frac{1}{\sqrt{2π}}e^{-\frac{x^2}{2}},S(x)=x,ψ(\theta)=\frac{θ^2}{2}$$
このような形だと何が嬉しいのかというと、\(ψ(\theta)\)が狭義の凸関数になるということです。
つまり、この確率密度関数の対数尤度関数は凹関数(上に凸)になります。
よって尤度方程式の解は(存在するならば)一意的で，それが最尤推定量となる。
このように，指数型分布族 は比較的扱いやすい統計モデルです。(停留点を求めると、それが最尤推定量になるということ)
最尤推定量については、以下をご覧くださいませ。
【実践】健康寿命と喫煙、肺の大きさ
2055年に亡くなった方の健康寿命を2040年時点から遡ってみました。 中でも、喫煙経験があった25人と25人の計50人を調査し、肺の大きさも測ります。 N:2040年から2055年までの年数。当然全員15年。 y:2040年から測った健康寿命。15以下。 x:腎臓の長さ s:喫煙因子/喫煙してるかしてないかの二択。 N:15 y:10 x:10.43 s:N 例：2050年までは健康に生きれたが2055年に亡くなった。肺の横の長さは10.43cm。喫煙経験はない人。
health<-read.csv("health.csv")
#データの読み込み
health$y
#健康寿命を表示
健康寿命をとりあえず出力してみました。平均すると2040年から7年くらいですね。
以下は簡単にグラフ化したものです。白の方が喫煙経験なしなので、ある程度健康寿命が伸びそうな傾向が見えます。
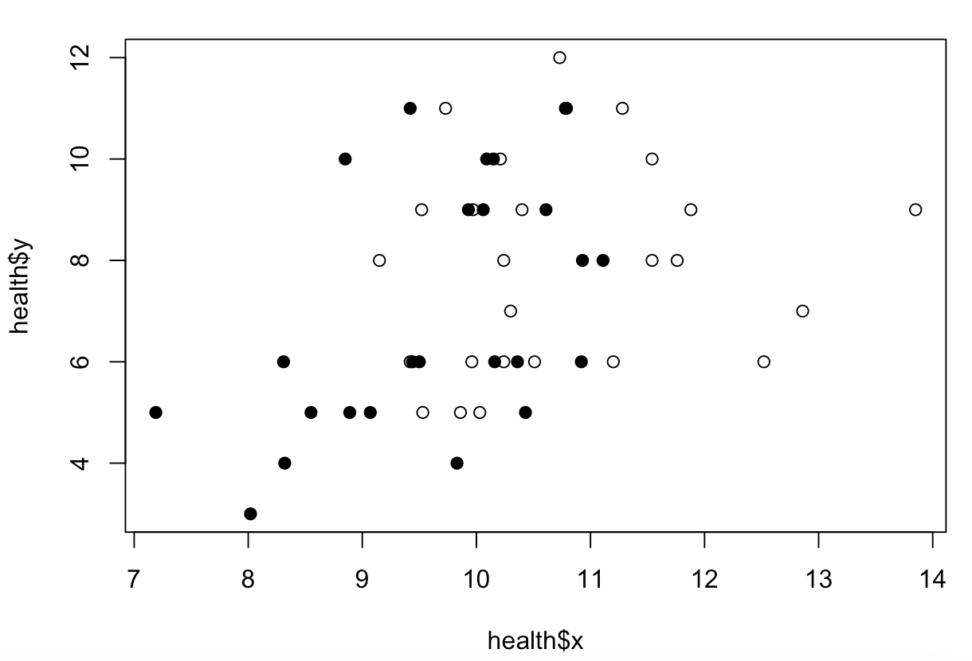
では分析を行います。
glm(cbind(y,N-y)~x+s,data=health,family=binomial)ばらつきの確率分布は、family=binomialで二項分布を使います。
応答変数に関しては、cbind(y,N-y)となっていますが、これはcbind(健康に生きれた年数、残りの健康に生きれなかった年数)を表しています。
$$(\hat{\beta_1}.\hat{\beta_2},\hat{\beta_3})=(-1.70356,0.17039,-0.08195)$$
\frac{q_i}{1-q_i}=exp(-1.70356+0.17039X_i-0.08195s)
$$log\frac{q_i}{1-q_i}=-1.70356+0.17039X_i-0.08195s$$
推定値としては、以上のようになります。
ロジスティック回帰からわかること
上の例で言うと、腎臓の大きさによる推定パラメータが0.17039でした。
つまり、個体iの腎臓の大きさが「1単位」増大すると、健康寿命のオッズは、
$$\frac{q_i}{1-q_i}=exp(-1.70356)exp(0.17039(X_i+1))exp(-0.08195s)$$
\(exp(0.17039)\)倍になることがわかります。
電卓で簡単に計算できますが、1.185767倍でした。
腎臓が大きい人は、ちょっと健康寿命が大きい傾向にあることがわかりました。
＊二項分布を使ったGLMで使われるリンク関数は、ロジットリンク関数だけでなく、プロビット関数など別の関数もあります。
ロジスティック回帰の場合には、リンク関数は、ロジット関数を使うというだけの話です。
