Python

HOME
Python
ブートストラップ法についてわかりやすく解説|R

05/31/2022 / 最終更新日時 : 11/26/2024 bluest Python

ブートストラップ法についてわかりやすく解説|R

ブートストラップ法(bootstrap method)

ブートストラップ法とは、限られた標本データから母集団の特性を推定するための統計的リサンプリング手法です。

特徴は、データの復元抽出による多数のサンプルセットの生成にあります。

重複を許して抽出する、というのがポイントです。

まずは、ブートストラップ法を使う目的を明確にしておきましょう。

目的

限られたデータセットから、母集団の統計的性質を推定する
モデルの不確実性や統計量の標準誤差を評価する

簡単に手順を説明するとこんな感じです。

元の標本データから、同じサイズのサンプルを復元抽出
復元抽出されたサンプルセットを複数生成
各サンプルセットで統計量を計算
得られた統計量の分布から、母集団の特性を推定

大事なのは、重複を許してサンプルから何度も抽出を行い、標準誤差を減らす、ということですね。

具体的なシナリオ

1000人の日本人女性が就業したかどうかがわかるデータが手元にあります。

このデータを使って、日本人女性全体の就業率を調べたいです。

復元抽出のイメージ

元のデータセット：1000人
各ブートストラップサンプル：1000人
特徴：
- 同じデータが複数回選ばれる可能性がある
- サンプルの組成は元のデータに近似

まず、

$$ε(A,B)$$

A：学習データ

B：テストデータ

これは、Bに対するAの逸脱度だとします。

逸脱度に関しては、【良いモデルとは】AIC(赤池情報量基準)について。をご覧ください。

$$ε(学習データ,母集団)$$

求めたい逸脱度は、母集団に対する学習データの誤り率です。

$$ε(学習データ,母集団) \leftrightarrow ε(学習データ,学習データ)$$

求められる逸脱度は上の図で言う右の誤り率です。右と左の差が分かれば、目的である「母集団に対する学習データの逸脱度」に近づきそうです。

ここで、ブートストラップサンプルを作ります。ただ復元抽出を行うだけです。

重複を許して、繰り返しサンプルを取ります。

例で言うと、集めた1000人の女性の就業状況データ(学習データ)を復元抽出し、1000人の女性のサンプルデータセットを複数作る(ブートストラップサンプル)ことができます。

学習データからn個復元抽出を行うと、n個のブートストラップサンプルを作ることができます。

$$ε(学習データ,学習データ) \leftrightarrow ε(BSサンプル,学習データ)$$

この学習データにおける学習データの逸脱度と、学習データにおけるブートストラップサンプルデータの逸脱度の差が分かれば、先ほどの求めたい差に近似できそうです。

なぜ近似できるかというと、復元抽出だとしても母集団と属性の割合は似てくるからです。

ただし無作為ならと言う条件は付きます。

母集団：大卒3000万人、高卒3000万人、その他500万人

学習データ/BSサンプル：大卒約450人、高卒約450人、その他約75人

この差を標準誤差と言います。

標準誤差について詳しく知りたい方は、【Standard Error】標準誤差を例題を通して解説。をご覧ください。

この逸脱度の差を1000回ほど繰り返して得てみると、逸脱度の差の分布がわかります。

ブートストラップ法の利点

ブートストラップ法は、限られたデータから母集団の特性を推定する統計的手法。

特に、サンプルサイズが小さく、理論的な分布が不明な場合に有効です。

なぜブートストラップ法で予測が改善されるのか

社会科学の分野では、上記のように復元抽出を繰り返すことで、標準誤差を把握することにブートストラップ法は使われます。

一方で、主に機械学習の分野では「データセットを複数作り、そこから作られるモデルを複数作成し、中間予測値を平均して、予測の改善を行う」と言う手法にも、ブートストラップ法は使われます。

統計の基本的な知識があれば、復元抽出の回数を増やせば増やすほど、予測が改善することが理解できるはずです。

ここでは、同じ確率分布から抽出される確率変数を$x_{b}$とおいています。

$$x_{ave}={\frac{\sum_{b}x_{b}}{B}}$$

上は、ブートストラップ法によって算出した実現値の平均値です。

平均値の分散は以下のように表すことができます。

$$E[(x_{ave}-E[x_{ave}])^2] = {\frac{Var(x_{b})}{B}}+{\frac{B-1}{B}}×corr(x_{b},x_{b’})×Var(x_{b})$$

第1項は分散をブートストラップ回数でスケールしたものです。

$X_{b}$に関しては、同一分布から発生していますが、独立であるとは限らないので、相関が発生します。これが第2項です。

ブートストラップ法による復元抽出を繰り返すと、第1項は0に近づくことがわかりますね。これは大数の弱法則です。

ただし、第2項は残ったままです。つまり特徴量同士の相関は残ると言うことです。

よく金融の分野では、分散投資をいくら行なっても、リスクは0にはならない理由として、各銘柄の株価が独立ではないことが挙げられます。

ブートストラップ法は分散には対処できますが、バイアスには大した対処はできないと言うことです。

【実践】Parametric Bootstrap法

今回は、パラメトリックなブートストラップ法をRで実践します。

パラメトリックとは、事前に母集団の確率分布がわかっている状態のことを指します。その分布を決定するパラメーターがわかれば、母集団分布について知ることができます。このパラメーターのことを「母数」と呼んでいます。また、逆の事前に母集団の確率分布がわかっていない状態のことを「ノンパラメトリック」と呼びます。

こちらのデータを使います。→【汎用性抜群】尤度比検定を解説します

「高卒と大卒、就業年数は年収と関係があるのか」という話です。

年収のデータは100個しかありません。

data <- read.csv("income.csv")
data$y

これをブートストラップ法で復元抽出しまくりましょう。

パラメーター数が少ない「大卒高卒かどうか考慮しないモデル」を帰無仮説としましょう。

$$logλ_{i} = β_{0}+β_{2}x_{i}+β_{2}c$$

β2=0と仮定されていることになります。

get.dd <- function(data){

  data$y.random <- rpois(nrow(data),lambda = mean(data$y))
  #平均が観測データの平均である、100個のポアソン乱数を生成します。
  
  fit1 <- glm(y.random ~ x, data=data, family = poisson)
  #帰無仮説のモデル
  
  fit2 <- glm(y.random ~ x+c, data=data, family = poisson)
  #対立仮説のモデル
  
  fit1$deviance - fit2$deviance
  #帰無仮説のモデルの残差から、対立仮説のモデルの残差を除く
  #逸脱度の差
  
}

get.dd

nrow(data)は、列数です。今回は100個です。

devianceはモデルの残差を表します。

帰無仮説と対立仮説の残差の差が、今回求めたかった逸脱度の差になります。

> fit1$deviance - fit2$deviance
[1] 0.5556915

出力結果は

0.05556915でした。これを1000回ほど繰り返していきましょう。

boots <- function(data,n.strap){

  replicate(n.strap,get.dd(data))

}
#boots：ブートストラップサンプルを作る関数を複製する関数

dd<-boots(data,n.strap = 1000)
#dd：bootsを1000回繰り返す

dd
#ddを出力

summary(dd)

summary()で統計量を見ましたが、よくわからないのでヒストグラムにしてみましょう。

hist(y)

P値(p value)

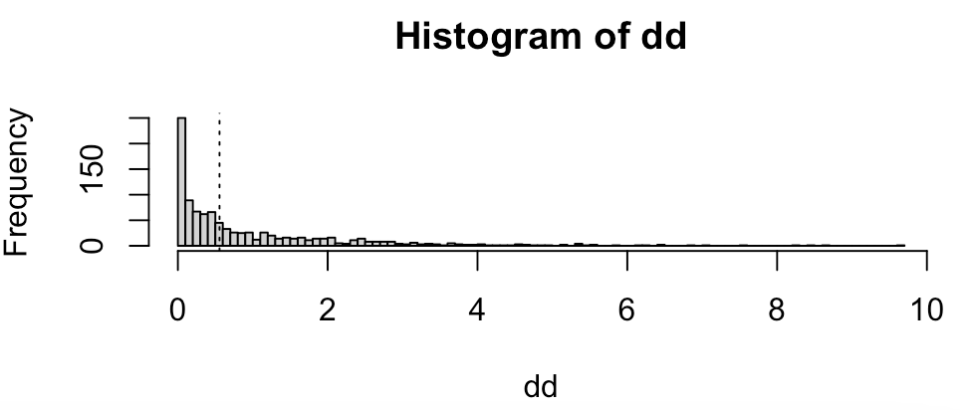
上の図は、先ほどの

0.5556915という逸脱度の差は分布のどの辺りに来るでしょうか？ablineで求めます。

abline(v=0.5556915,lty = 3)

summary(dd >= 0.5556915)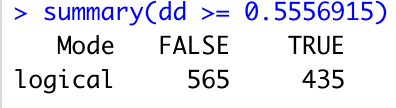

435/1000より、p値としては0.435となりました。これは大きすぎますので、棄却できません。

p値については、以下のコンテンツで解説しております。

結果：帰無仮説は棄却できないので、${\beta 3=0}$かどうかよくわからない。

今回は、100個のデータだけ使って復元抽出を行う「ブートストラップ法」を行いました。

モデルを比較する方法はいくつもあるので、この機会に勉強してみてください。

補足｜バギングとランダムフォレスト(bagging & random forest)

バギングは、機械学習におけるアンサンブル学習の手法の一つで、ブートストラップ法を機械学習に応用した代表的な手法です。その主な目的は、モデルの分散を減らし、予測精度を向上させることにあります。

バギングの基本的な手順は以下の通りです

データの復元抽出 元のデータセット $D$ から、同じサイズの複数のブートストラップサンプル $D_1, D_2, …, D_k$ を作成します。各サンプルは元のデータから復元抽出されるため、同じデータが複数回選ばれる可能性があります。
個別モデルの学習 それぞれのブートストラップサンプル $D_i$ を用いて、同じ種類の弱学習器（例：決定木）を独立に学習させます。
予測の統合 分類問題では多数決、回帰問題では平均値を取ることで、最終的な予測を行います。

$${\hat{f}(x) = \frac{1}{k}\sum_{i=1}^k \hat{f}_i(x)}$$

そして、ランダムフォレストは、バギングをさらに発展させた機械学習アルゴリズムです。

決定木を基本モデルとし、以下の2つの特徴を持っています

データのブートストラップサンプリング バギングと同様に、元のデータセットから復元抽出を行います。
特徴量のランダム選択 各決定木の学習時に、全特徴量の一部（$m$個）をランダムに選択し、その中から最適な分割特徴量を選びます。通常、分類問題では $m = \sqrt{p}$、回帰問題では $m = p/3$（$p$は全特徴量数）が経験的によく用いられます。

ブートストラップ法とは違い、特徴量も復元抽出を行うのがランダムフォレストの特徴です。強力な予測力を持つ特徴量を使わない決定木があると、普段使われなかった特徴量がノードの分岐に使われます。これによって、予測の改善や計算時間の短縮につながります。