Python

HOME
Python
【python】カーネルSVMとは？kernel関数を利用した非線形データの判別問題に挑戦|機械学習

03/30/2023 / 最終更新日時 : 11/19/2023 bluest Python

【python】カーネルSVMとは？kernel関数を利用した非線形データの判別問題に挑戦|機械学習

こんにちは、青の統計学です。

今回は、判別タスクに関わる解決手法「カーネルSVM」をご紹介します。

判別タスクは、決定木やロジスティック回帰、線型SVM、k近傍法などたくさんあります。

カーネルSVMの特徴は、非線形データに対応することができる点にあります。可視化や数学的手法まで掘り下げていきますので、ぜひご覧ください。

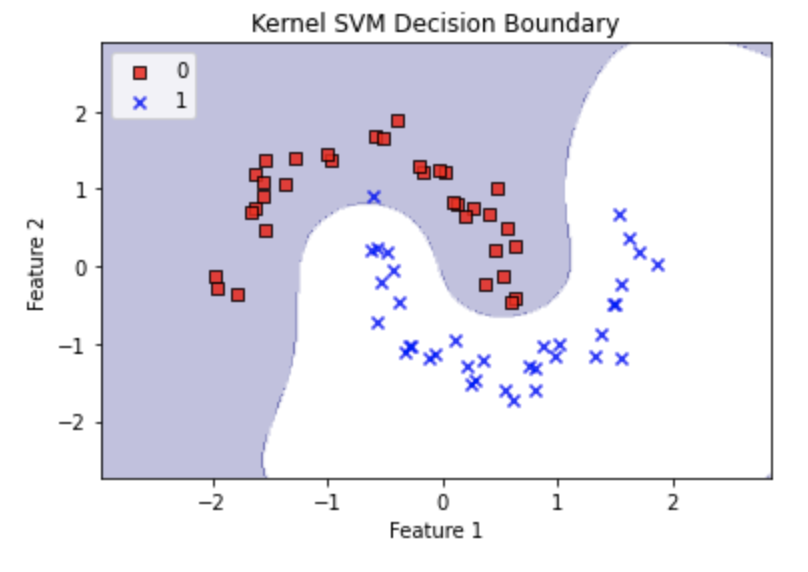
カーネルSVM(kernel support vector machine)

サポートベクターマシン（SVM）は、分類問題を解決するための強力な機械学習手法です。

カーネルSVM（Kernelized Support Vector Machine）は、サポートベクトルマシンの拡張であり、線形分離できないデータを扱うことができます。

カーネルトリックと呼ばれるテクニックを利用して、高次元空間にマッピングし、線形分離可能になることが特徴です。

普通のサポートベクトルマシンについては以下のコンテンツをご覧ください。

【判別問題】サポートベクトルマシン(SVM)の仕組み|python

数学的背景

カーネルSVMの背後にある数学的な考え方は、データを高次元空間に変換して、線形分離を可能にすることです。

以下のようなカーネル関数を用いて、元の特徴空間から高次元空間への変換を行います。

$$k(\boldsymbol{x}, \boldsymbol{y}) = φ(x)・φ(y)$$

というか、カーネル関数を使って高次元にするとはどういうことなのでしょうか？

カーネル関数とは何か、詳しく解説

カーネル関数 k(x, y) は、2つのデータ点 x と y の類似度を測る関数です。

$$k(x, y) = φ(x)・φ(y)$$

ここで、φ(x) はデータ点 x(特徴量ベクトルです) を元の特徴空間から高次元の特徴空間へ変換する(ように振る舞う)関数です。

実際にはデータを高次元空間に変換しなくても、元の特徴空間でのデータ点のペアの類似度（内積）をカーネル関数を使って計算することができる技巧です。

カーネル関数は、あたかもデータが高次元空間に変換されたかのように振る舞いますが、実際にはデータの変換を行わずに計算ができるため、計算コストを大幅に削減できます。

この技巧をカーネルトリックと呼びます。

この性質により、カーネル関数を用いることで、高次元の特徴空間での内積 φ(x)・φ(y) を計算することができます。

この内積は、類似度の指標として解釈できます。

内積はCNN(畳み込みニューラルネットワーク)やコサイン類似度など、機械学習の分野で多く登場するアイディアで、二つのベクトルがどれだけ類似しているかを定量的に判断できます。

【python】畳み込みニューラルネットワークによる画像判別プログラムの開発

【python】コサイン類似度は高校数学の知識で理解できます！|自然言語処理

カーネルトリックとは

カーネルトリックは、カーネル関数を用いて高次元空間での内積を直接計算することで、実際にデータを高次元空間に変換することなく、非線形分類器を学習させることができます。

[例]あるデータセットにおいて、データ点Aとデータ点Bがあり、それぞれに対応する特徴ベクトルが存在します。

カーネル関数は、データ点Aとデータ点Bの特徴ベクトルを入力として受け取り、それらの類似度を計算する役割を果たします。

類似度をどう測るかは、カーネル関数次第です。

→類似度が、サポートベクトル(決定境界上の点)の発見に役立ち、高次元特徴空間で決定境界を引いたように見えるわけです。

代表的なカーネル関数には、線形カーネル、多項式カーネル、RBFカーネル（動径基底関数カーネル）などがあります。

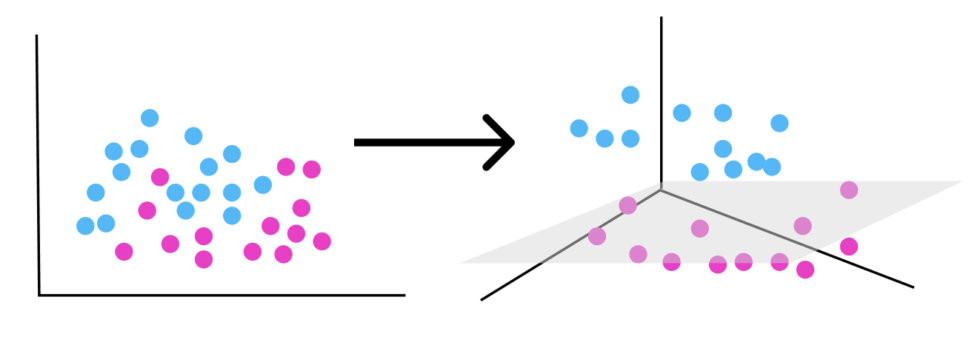
(例：二次元では線形で決定境界が引けないデータでも次元を上げれば、線形で境界が引けるかも!??→元の次元に戻す)

線型カーネル（Linear Kernel）: $K(\boldsymbol{x}, \boldsymbol{y}) = \boldsymbol{x} \cdot \boldsymbol{y}$

線形カーネルは、データが線形分離可能な場合に有効です。

多項式カーネル（Polynomial Kernel）: $K(\boldsymbol{x}, \boldsymbol{y}) = (\boldsymbol{x} \cdot \boldsymbol{y} + c)^d$

多項式カーネルは、特徴空間の次数を増やすことで非線形性を捉えられます。

RBFカーネル（Radial Basis Function Kernel）: $K(\boldsymbol{x}, \boldsymbol{y}) = \exp{(-\gamma ||\boldsymbol{x} – \boldsymbol{y}||^2)}$

RBFカーネルは、非線形問題に広く適用されており、パラメータ調整が比較的容易です。

これが一番使われていますね。ユークリッド距離の2乗にパラメータガンマがかけられています。

ガウスカーネルと呼ばれたりします。

シグモイドカーネル（Sigmoid Kernel）: $K(\boldsymbol{x}, \boldsymbol{y}) = \tanh{(\alpha \boldsymbol{x} \cdot \boldsymbol{y} + c)}$

シグモイドカーネルは、ニューラルネットワークの活性化関数と類似しており、その性質を利用できます。

ロジスティック回帰の活性化関数としてシグモイド関数が使われていますね。

シグモイド関数は、-∞から+∞の実数を0から1の値に変換します。

CODE|python

今回は、線形の決定境界では分類が難しいデータを使って、カーネルSVMの破壊力を見てみましょう。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC

# 非線形データセットの生成
X, y = datasets.make_moons(n_samples=100, noise=0.1, random_state=1)

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)

# 標準化
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)

# カーネルSVMの学習 (RBFカーネル)
svm = SVC(kernel='rbf', C=1.0, gamma=0.1, random_state=1)
svm.fit(X_train_std, y_train)

# 決定境界のプロット
def plot_decision_regions(X, y, classifier, resolution=0.02):
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = plt.cm.get_cmap('terrain', len(np.unique(y)))
    
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
                    alpha=0.8, color=colors[idx],
                    marker=markers[idx], label=cl,
                    edgecolor='black')

plot_decision_regions(X_train_std, y_train, classifier=svm)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(loc='upper left')
plt.title('Kernel SVM Decision Boundary')
plt.show()

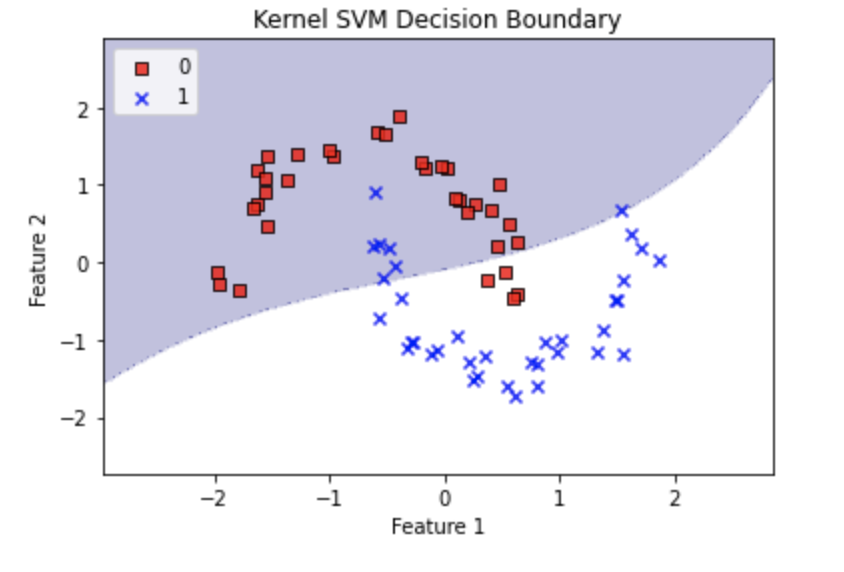
さて、決定境界が線形に近く、今回のデータをうまく分類できているとは言えませんね。

どのハイパーパラメータをチューニングすべきでしょうか。

答えは、gammaです。

カーネルSVMにおいて、非線形具合を増すために調整すべき主要なパラメータは gamma です。

RBFカーネル（Radial basis function kernel、動径基底関数カーネル）を使用している場合、gammaはカーネル関数の形状を制御します。

gammaの値が大きいほど、決定境界はより複雑になります。

逆に、gammaの値が小さいと、決定境界はより線形に近くなります。

$$K(\boldsymbol{x}, \boldsymbol{y}) = \exp{(-\gamma ||\boldsymbol{x} – \boldsymbol{y}||^2)}$$

一旦ガウスカーネルの関数を見返してみましょう。

ここで、x と y はデータ点で、||x – y|| はユークリッド距離を表します。

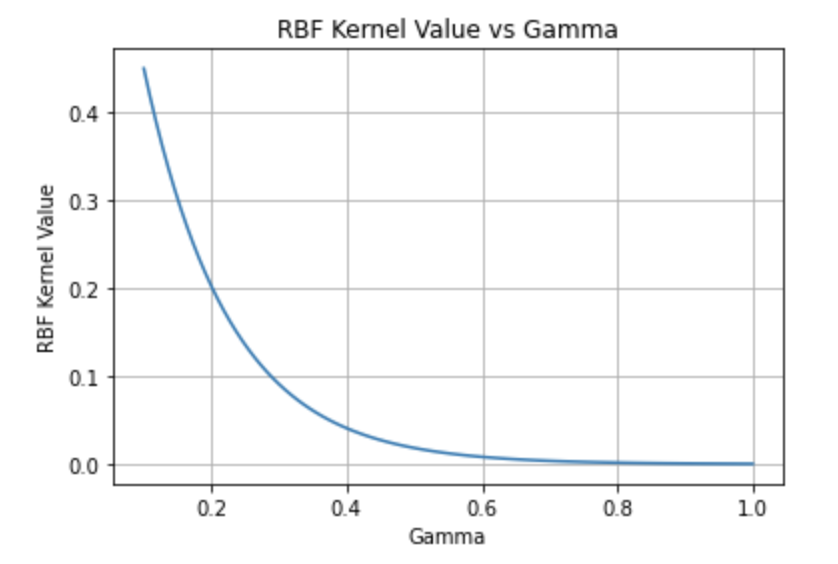
gamma の値が大きい場合： カーネル関数の値は、データ点が互いに離れていると急速に0に近づきます。

これは、カーネルが「鋭い」形状を持つことを意味し、SVMが学習する決定境界がより複雑になります。

この場合、モデルはデータの細かい構造に適応しやすくなりますが、過学習のリスクが高まります。

gamma の値が小さい場合： カーネル関数の値は、データ点が離れていても緩やかに減少します。

これは、カーネルが「滑らか」な形状を持つことを意味し、SVMが学習する決定境界はより線形に近くなります。

この場合、モデルはデータの細かい構造に適応しにくくなりますが、過学習のリスクは低くなります。

ちなみにガウスカーネルのもう一つのパラメータCは正則化パラメータです。

以下の例では、gamma を 1に設定しています。

これにより、非線形具合が増し、より複雑な決定境界が描かれます。

# カーネルSVMの学習 (RBFカーネル、gamma=5)
svm_high_gamma = SVC(kernel='rbf', C=1.0, gamma=1, random_state=1)
svm_high_gamma.fit(X_train_std, y_train)

# 決定境界のプロット
plot_decision_regions(X_train_std, y_train, classifier=svm_high_gamma)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(loc='upper left')
plt.title('Kernel SVM Decision Boundary (High Gamma)')
plt.show()