コサイン類似度とは?高校数学で理解する
1. コサイン類似度とは?
ベクトル同士の“方向の近さ”を測る指標
コサイン類似度(Cosine Similarity)とは、主に2つのベクトルがどのくらい同じ方向を向いているかを測定するための指標です。計算結果の値は-1から1の範囲をとり、
- 1に近いほど「同じ方向を向いている」(非常に類似している)
- 0に近いほど「直交している」(似ていない)
- -1に近いほど「正反対を向いている」(まったく異なる)
という解釈ができます。
高校数学レベルの“ベクトルのなす角”がベース
コサイン類似度の根本は、高校数学でも学ぶベクトルの内積や、なす角${\theta}$と${cos \theta}$の関係を利用しているため、文系・理系を問わず比較的わかりやすいのが特徴です。
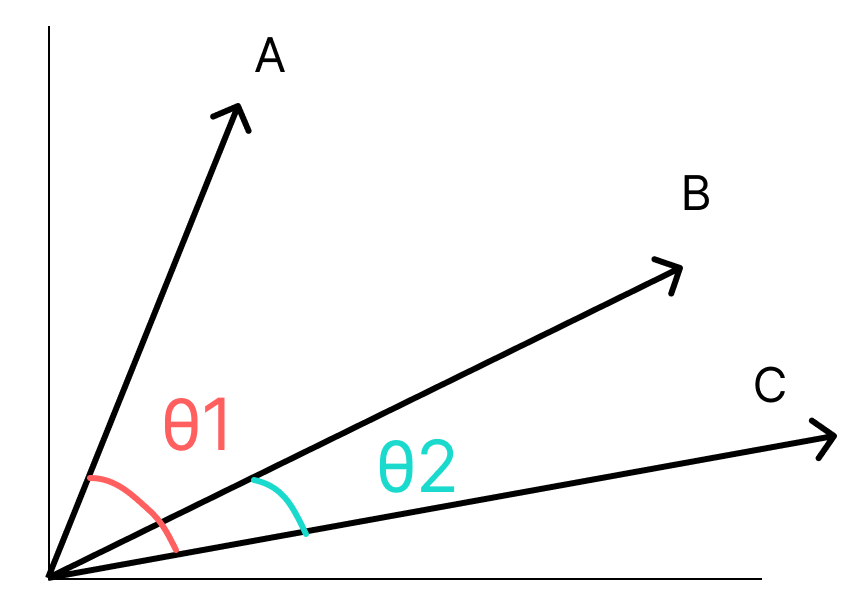
2. コサイン類似度の計算式と具体例
計算式
$${\text{Cosine Similarity}(A, B) = \frac{A \cdot B}{\|A\| \times \|B\|}}$$
- ${A \cdot B}$ : ベクトル${A}$と${B}$の内積
- ${\|A\|}$ : ベクトル${A}$の大きさ(ユークリッドノルム)
- ${\|B\|}$ : ベクトルBBBの大きさ(ユークリッドノルム)
例:2次元ベクトル
- ${A = (2, 8)}$
- ${B = (5, 6)}$
上記とすると、
$${A \cdot B = 2 \times 5 + 8 \times 6 = 10 + 48 = 58}$$
正規化ノルムは以下のようになるので、
- ${\|A\| = \sqrt{2^2 + 8^2} = \sqrt{4 + 64} = \sqrt{68}}$
- ${\|B\| = \sqrt{5^2 + 6^2} = \sqrt{25 + 36} = \sqrt{61}∥B∥=52+62=25+36=61}$
$${\text{Cosine Similarity}(A, B) = \frac{58}{\sqrt{68} \times \sqrt{61}} \approx 0.90}$$
この結果、コサイン類似度は約0.90と高めであることがわかります。
3. コサイン類似度のメリットとデメリット
メリット
- スケールに左右されにくい
ベクトルの方向のみを考慮するため、文書や画像ベクトルの“長さ”が異なっていても比較可能です。 - 高次元かつスパースなデータに強い
文字数の多い・少ない文書でも処理しやすく、NLPなどで一般的に使用されます。 - 計算コストが比較的低い
内積とノルム(ベクトルの大きさ)の計算だけなので、大規模データにも適用しやすいです。
デメリット
- ベクトルの大きさ(絶対値情報)を無視
大きさの違いが重要な場合には向かず、場合によっては有益な情報を逃す恐れがあります。 - 負の値をどう解釈するか
コサイン類似度は-1も取り得ますが、そのケース(角度が90度を超えた場合)をどのように扱うかは応用先で工夫が必要です。 - 高次元の呪い
ものすごく次元が高いデータ(数万〜数十万次元)では、ほとんどのベクトルが直交に近くなり、数値の扱いが難しくなる場合があります。

詳しくは後述しますが、コサイン類似度が抱える「解の不定性」や「意味的類似度として妥当なのか」を立ち止まって考えたいですね。
4. 実際にPythonで実装
4.1 Scikit-learnでの実装例
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
# ベクトルAとBを用意
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])
# 2次元に変形してcosine_similarityに投げる
A = A.reshape(1, -1)
B = B.reshape(1, -1)
# コサイン類似度を計算
cos_sim = cosine_similarity(A, B)
print(f"Cosine Similarity: {cos_sim[0][0]}")
- 出力される値が1に近いほど似ていると言えます。
4.2 NumpyやSciPyでの実装例
import numpy as np
from numpy.linalg import norm
def cosine_similarity_manual(vec1, vec2):
return np.dot(vec1, vec2) / (norm(vec1) * norm(vec2))
A = np.array([0, 1, 3, 3, 5])
B = np.array([3, 2, 0, 1, 2])
result = cosine_similarity_manual(A, B)
print(result)4.3 gensimによるNLP実装例
以下は、2つの英語文書をBag of Words形式でベクトル化した上で、コサイン類似度を求める例です
from sklearn.metrics.pairwise import cosine_similarity
import gensim
import gensim.corpora as corpora
# サンプル文書
text1 = "I love playing soccer"
text2 = "I enjoy playing football"
# 小文字化&分割
text1 = text1.lower().split()
text2 = text2.lower().split()
# 辞書を作成
dictionary = corpora.Dictionary([text1, text2])
# Bag of Words形式へ
vec1 = dictionary.doc2bow(text1)
vec2 = dictionary.doc2bow(text2)
# gensimのベクトルを疎→密に変換
vec1 = gensim.matutils.sparse2full(vec1, len(dictionary))
vec2 = gensim.matutils.sparse2full(vec2, len(dictionary))
# コサイン類似度の計算
sim = cosine_similarity([vec1], [vec2])[0][0]
print(sim)5. 具体的なケーススタディ・導入事例
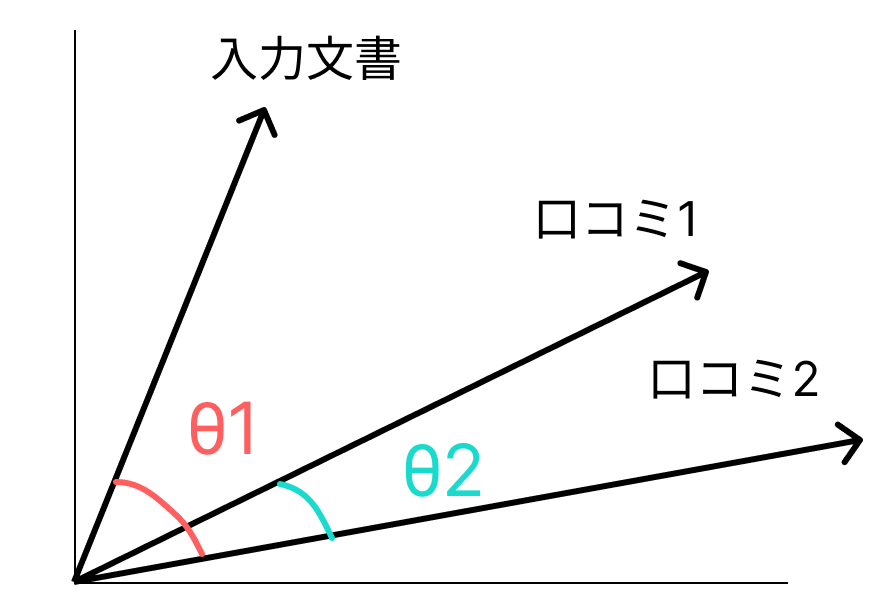
類似文章の探索などでよく使いますが、他にも使える事例はあります。
| ケーススタディ | データ | 方法 | 結果・用途 |
|---|---|---|---|
| 文書類似度 | テキスト文書 | コサイン類似度 | 剽窃検出、文書分類、クラスタリングなど |
| レコメンデーションシステム | ユーザーの読書履歴 | コサイン類似度 | 類似した書籍や商品のレコメンド |
| 画像認識 | 画像の特徴ベクトル | コサイン類似度 | 類似画像検索、顔認証 |
| 検索エンジン | 検索クエリ & 文書 | コサイン類似度 | 関連性の高い文書をランキング |
| 履歴書マッチング | 履歴書 & 職務記述書 | コサイン類似度 | 候補者と求人の適合度評価 |
| 剽窃検出 | 文書 & 文書 | コサイン類似度 | 内容が酷似している文書を自動検出 |
6. 応用|コサイン類似度の課題
ちょっとデメリットでもまとめましたが、コサイン類似度の万能ではない点を語っていきます。
詳しくは、こちらの論文がおすすめです。
さて、コサイン類似度(Cosine Similarity)は、高次元ベクトル間の向きの近さを定量的に測る指標として広く使われています。とくに、上の事例でまとめている通りで単語ベクトル・アイテム埋め込み・ユーザー埋め込みなどの「埋め込み(embedding)」が得られた後、その間の類似度を測る際に常套手段として用いられます。
- 自然言語処理(NLP):Word2VecやBERTなどで得られた単語・文書ベクトル同士の類似度
- レコメンデーション:ユーザー埋め込みとアイテム埋め込み間の類似度
- 画像認識:画像特徴ベクトル間の類似度
- 各種クラスタリングや近傍検索 など
しかし、コサイン類似度を
- 意味的な近さ
- 数値としての近さ
がイコールであるかのように解釈してしまうのは危険である、という注意点があります。
具体的にみていきましょう。
7. コサイン類似度の限界:埋め込みのスケール不変性が生む問題
7.1 埋め込みベクトルのスケール調整とその恣意性
コサイン類似度は、次のように角度のコサイン値によって類似度を測ります
$${\text{CosSim}(\mathbf{u}, \mathbf{v}) = \frac{\mathbf{u} \cdot \mathbf{v}}{\|\mathbf{u}\|\|\mathbf{v}\|}}$$
${\mathbf{u}}$ と ${\mathbf{v}}$ はベクトル
これはベクトルの大きさ(ノルム)を取り除いて方向のみを評価します。一見すると、文書長やアイテムの人気度によるスケールの違いを除去できるため便利ですが、逆に「スケールをどう扱ってもコサイン類似度は変わらない」という性質が裏目に出ることがあります。

例えば、同じ方向を向いているベクトルAとBがあったとき、ベクトルBを2倍大きくしてもコサイン類似度は同じです。この2倍というスケーリング自由度を学習過程で恣意的に操作できてしまうと、本来の意味的類似度とは別次元の理由で大きく数値が変わる可能性があります。
7.2 方向のみに注目するがゆえの弊害
とくに学習によって得られる埋め込みベクトルは、複数次元にわたるスケール要素を含んでいます。たとえば、行列分解の観点では、各特異値(Singular Value)の取り方や、学習係数の調整などによって埋め込み空間全体のスケーリングが恣意的に変化し得ます。
その結果、モデルのパラメータ(埋め込みベクトル)が変化しても、コサイン類似度自体の値はまったく別物になってしまう場合があり、ユーザーやアイテム同士の類似性ランキングがバラバラになることがあります。
8. コサイン類似度を活用する上での注意点
- ベクトルの正規化
コサイン類似度では自動的に正規化された効果を得られますが、事前にベクトルをL2正規化などで揃えておくと、より安定した比較ができます。 - 次元削減の活用
PCAやSVD、あるいはWord Embedding(Word2Vec, GloVe など)を使うと、高次元の呪いを軽減しつつ、コサイン類似度の有用性を生かせます。 - 負の値の解釈
ベクトル同士が90度を超えると、コサイン類似度は負になります- 応用先によっては、負の値を切り捨てて0とするなど、ビジネスロジックに合わせた扱い方を検討しましょう。
- 複雑な非線形関係には別途アプローチ
コサイン類似度は線形な関係性しか捉えられないため、深層学習ベースのモデルやソフトコサインなど、他のアプローチと組み合わせると精度が上がるケースがあります。
まとめ!
コサイン類似度は、「2つのベクトルがどの程度似ているか」を定量的に測る指標です。
- 方向のみを重視するため、大きさに左右されにくく、文書や画像のように長さが異なるデータ比較に向いています。
- NLPやレコメンドエンジン、画像検索など、広い分野で実績があり、多くのライブラリで簡単に計算可能
- 一方、負の値や高次元の呪いに対する対策が必要になる場面もある。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


