勾配ブースティング決定木(GBDT)の仕組みを理解|XGBoostとLightGBMの違いを理解する
はじめに
こんにちは、青の統計学です。
今回は、Kaggle等の機械学習のコンペでもよく使われる、勾配ブースティング決定木(Gradient Boosting Decision Tree, GBDT)について仕組みから理解していこうと思います。
決定木やランダムフォレストとの比較もしながら、使い分けもできるようにしていきましょう。
決定木からアンサンブル学習への系譜
GBDTを理解するために、その構成要素である決定木(Decision Tree)と、複数の学習器を組み合わせるアンサンブル学習の考え方を整理していきましょう。
決定木の弱点とアンサンブル学習について
決定木は、データを質問形式で分割していくため、解釈性が高いという利点があります。しかし、深く成長させすぎると、訓練データに過剰に適合してしまう過学習(Overfitting)を起こしやすいという根本的な弱点があります。

これは、統計学でいうところのバリアンス(分散)が大きい状態、つまりデータが少し変わるだけで予測結果が大きくブレてしまう不安定さを意味します。
この不安定さを克服するために生まれたのがアンサンブル学習です。アンサンブル学習には大きく分けてバギング(Bagging)とブースティング(Boosting)の二つの戦略があります。
| 特徴 | バギング(例:ランダムフォレスト) | ブースティング(例:GBDT) |
| 学習の進め方 | 並列的 | 逐次的(直列的) |
| 目的 | 分散(バリアンス)の低減 | バイアス(系統誤差)の低減 |
| 学習器の性質 | 強い学習器(過学習気味) | 弱い学習器(精度が低い) |
| 最終予測 | 多数決や平均 | 弱学習器の重み付き和 |
ランダムフォレストはバギングの代表例であり、複数の強い決定木を並列に作り、その予測を平均することで、個々の木の過学習を打ち消し合い、分散を低減します。
一方、GBDTが採用するブースティングは、逐次的に学習器を構築します。前の学習器が間違えた部分(つまり誤差)を次の学習器が重点的に学習することで、モデル全体のバイアス(系統誤差)を低減し、予測精度を高めることを目指します。
勾配ブースティング(Gradient Boosting)の数学的背景
ブースティングの核となる考え方は「残差を学習する」ことです。しかし、GBDTはこれをさらに一般化し、統計学で学んだ勾配降下法(Gradient Descent)の枠組みで捉え直します。

これが「勾配ブースティング」と呼ばれる所以です。
残差は負の勾配の特殊なケースという話
回帰問題(数値を予測する問題)において、私たちが最小化したいのは、通常、二乗誤差をベースとした損失関数 $L(y, F(x))$ です。
ここで、現在の予測モデルを $F_{m-1}(x)$ とし、次の弱学習器 $h_m(x)$ を加えることで、より良いモデル $F_m(x)$ を構築したいと考えます。
$$F_m(x) = F_{m-1}(x) + \nu h_m(x)$$
ここで $\nu$ は学習率(Learning Rate)です。
勾配降下法では、目的関数を最小化するために、現在の地点から最も急な下り坂、すなわち勾配の逆方向に移動します。GBDTでは、この「急な下り坂」の方向を、次の弱学習器 $h_m(x)$ に学習させます。
具体的には、次の弱学習器は、現在の予測 $F_{m-1}(x)$ における損失関数 $L$ の負の勾配を近似するように学習します。
$$g_m(x) = – \left[ \frac{\partial L(y, F(x))}{\partial F(x)} \right]_{F(x) = F_{m-1}(x)}$$
この $g_m(x)$ が、GBDTにおける学習すべきターゲットとなります。
もし損失関数が最もシンプルな二乗誤差$L(y, F(x)) = \frac{1}{2}(y – F(x))^2$ であった場合を考えてみましょう。
$$g_m(x) = – \left[ \frac{\partial \frac{1}{2}(y – F(x))^2}{\partial F(x)} \right]_{F(x) = F_{m-1}(x)} = – \left[ (y – F(x)) \cdot (-1) \right]_{F(x) = F_{m-1}(x)} = y – F_{m-1}(x)$$
つまり、二乗誤差の場合、負の勾配は残差(正解値 $y$ と現在の予測 $F_{m-1}(x)$ の差)と一致します。

つまり、GBDTの本質は、残差学習を二乗誤差以外のあらゆる損失関数に適用できるように、勾配降下法という数学的な枠組みで一般化したものなのです。
逐次的な学習のイメージ
GBDTは、この負の勾配(一般化された残差)をターゲットとして、決定木を一つずつ追加していきます。
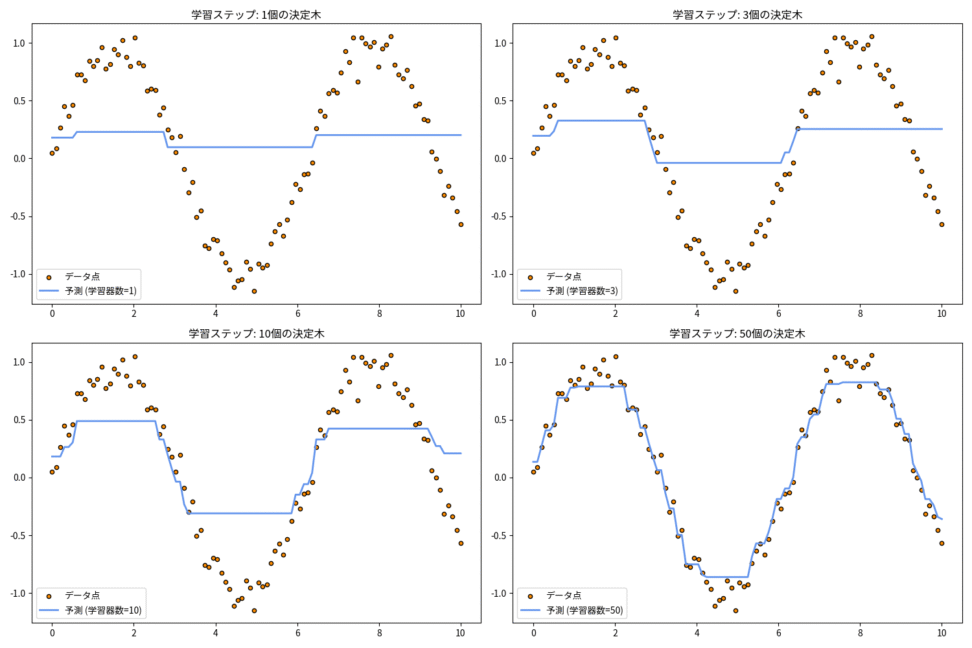
上の図は、学習器の数が増えるにつれて、モデルの予測曲線が徐々にデータ点にフィットしていく様子を示しています。個々の決定木は単純な形(弱い学習器)ですが、それらが協力し合うことで、最終的に複雑で高精度な予測を実現します。
GBDTのアルゴリズム:決定木をどう積み上げるかという話
GBDTのアルゴリズムは、以下のステップを繰り返すことで成り立っています。
- 初期値の設定: 最初の予測 $F_0(x)$ を、損失関数を最小化する定数(例えば、回帰なら目的変数の平均)で設定します。
- 負の勾配の計算: $m$ 番目のステップにおいて、現在の予測 $F_{m-1}(x)$ を用いて、各データ点における損失関数の負の勾配 $g_m(x)$ を計算します。
- 弱学習器の学習: 新しい決定木 $h_m(x)$ を、ターゲット $g_m(x)$(負の勾配)を予測するように学習させます。
- モデルの更新: 学習率 $\nu$ を用いて、モデルを更新します。
- $$F_m(x) = F_{m-1}(x) + \nu h_m(x)$$
- 繰り返し: ステップ2〜4を、所定の学習器の数に達するまで繰り返します。
このプロセスにおいて、学習率 $\nu$ は重要な役割を果たします。$\nu$ を小さく設定すると、一歩一歩の補正が小さくなるため、より多くの決定木が必要になりますが、過学習を防ぎ、汎化性能の高いモデルが得られやすくなります。

これは、統計学における正則化の考え方と似ていませんかね
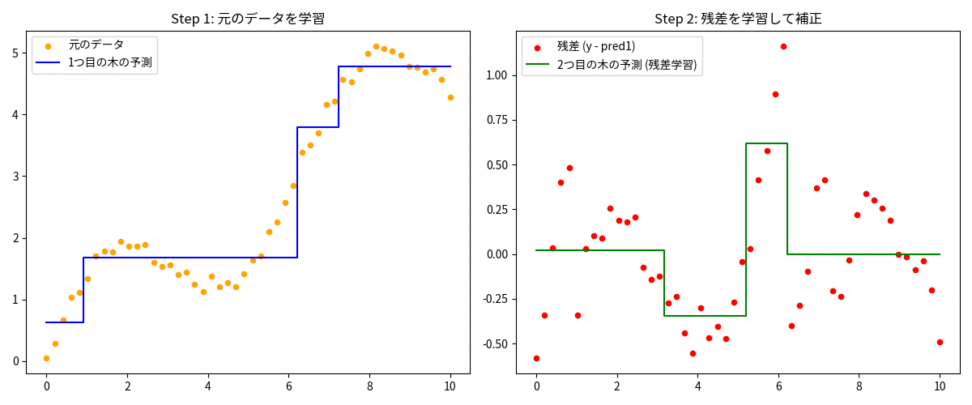
上の図の左側は、最初の決定木が元のデータを大まかに学習した様子、右側は、その予測と正解の差である「残差」を、次の決定木が学習している様子を示しています。このように、GBDTは残された誤差に焦点を当てて、モデルを段階的に改善していくことで、高い精度を達成します。
XGBoostとLightGBM
基本的なGBDTのアルゴリズムは強力ですが、計算効率や精度向上のために、様々な改良が加えられてきました。その代表格が、XGBoostとLightGBMです。
XGBoost (eXtreme Gradient Boosting)
XGBoostは、GBDTのアルゴリズムに正則化項を導入し、さらに2次近似(テイラー展開)を用いて損失関数を最適化することで、より厳密な解を求めることを可能にしました。
- 2次近似: 損失関数を2次までテイラー展開することで、より正確な最適化を実現し、高い予測精度に貢献しています。
- 正則化: 決定木の複雑さ(葉の数や出力値の大きさ)に対してペナルティを課すことで、過学習を強力に抑制します。
- 並列処理: 決定木の構築プロセスにおいて、各ノードの最適な分割点を探す処理を並列化することで、計算速度を大幅に向上させました。
LightGBM
LightGBMは、Microsoftが開発したGBDTのフレームワークであり、XGBoostの成功を受けて、特に大規模データと高速性に焦点を当てて改良されました。
LightGBMの最大の特徴は、決定木の成長戦略にあります。
Leaf-wise(葉単位)の成長
XGBoostがLevel-wise(レベル単位)、つまり木の深さが同じになるようにノードを分割していくのに対し、LightGBMはLeaf-wiseを採用します。Leaf-wiseは、最も損失の減少が大きい葉を優先的に分割していくため、同じ計算量であれば、より早く損失を最小化する方向に進みます。これにより、学習速度が劇的に向上しますが、一方で、小さなデータセットでは過学習しやすくなる傾向もあります。
GOSS (Gradient-based One-Side Sampling)
勾配(残差)が大きいデータ点(つまり、現在のモデルが予測を大きく間違えているデータ点)を優先的にサンプリングして学習に用いる手法です。これにより、すべてのデータを使わなくても、効率的にモデルを改善できます。
EFB (Exclusive Feature Bundling)
互いに排他的な特徴量(同時に非ゼロにならない特徴量)を束ねて一つの特徴量として扱うことで、特徴量の数を減らし、計算を高速化します。
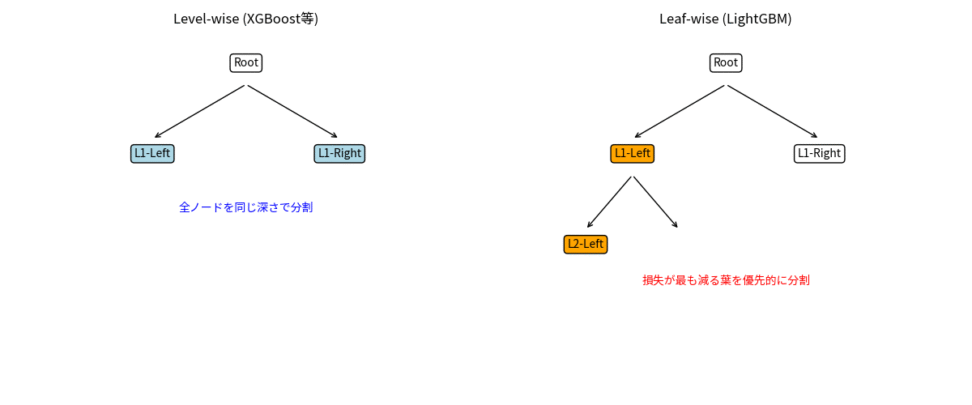
上の図は、XGBoostのLevel-wiseが慎重で安定した成長(左)であるのに対し、LightGBMのLeaf-wiseが積極的で効率的な成長(右)であることを示しています。
決定木・ランダムフォレスト・GBDTの使い分け
ここまで見てきたように、決定木、ランダムフォレスト、GBDTは、それぞれ異なる特性を持っています。どの手法を選ぶかは、データの性質、計算リソース、そして重視する要素(精度、速度、解釈性)によって決まります。
| 手法 | 予測精度 | 学習速度 | 解釈性 | 過学習への耐性 | 最適な利用シーン |
| 決定木 | 低 | 高 | 高 | 低 | 意思決定プロセスの可視化、小規模データ |
| ランダムフォレスト | 中〜高 | 中 | 中 | 高 | 安定性が求められるタスク、ベースラインモデル |
| GBDT (XGB/LGBM) | 高 | 高 | 低 | 中 | 予測精度が最優先のタスク、大規模データ |
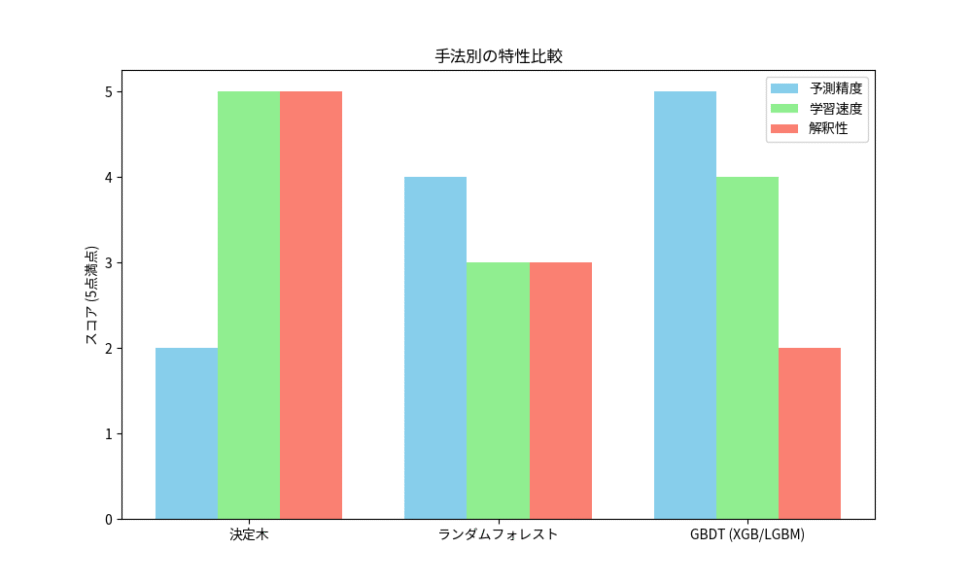
比較が示すように、GBDT系アルゴリズムは、高い予測精度と実用的な学習速度を両立させています。

つまり、予測精度を追求するならGBDT系、モデルの仕組みを人に説明する必要があるなら決定木、安定性を重視するならランダムフォレスト、という使い分けが基本となりますね。
この記事でGBDTに興味が出た人は、GBDTのカテゴリ変数処理を改善したCatBoostや、ハイパーパラメータの最適化を自動で行うOptunaなどのツールも触ってみてください。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!




