【kaggle】ベイズ最適化とXGBでtitanicの予測問題を解く|python
今回はハイパーパラメータのチューニング手法の一つである、ベイズ最適について解説いたします。
グリッドサーチやランダムサーチに比べて、短い時間で最適なパラメータを発見できるとされています。
また、今回はデータ分析コンペのkaggleのtitanicのデータを使っています。
ベイズ最適化(Bayesian Optimization)
結論から言えば、ベイズ最適化とは「点xにおける関数f(x)の値を観測し、全体のf(x)の形状を推定する」手法です。
そして、なるべく少ない数のf(x)を観測してf(x)の形を把握したいので、ガウス過程回帰という方法を使って、観測するf(x)を決定しています。
よく例えられるのが、以下のような例です。
「天井が見えない洞窟の形を知りたい」 Aさんはある位置pから真上に向かって石を投げる →数秒後に天井に石がぶつかって音が鳴ります。 →地上からの距離がわかる。 →石を投げる位置をずらして、洞窟の形状を理解していく。
イメージは掴めたでしょうか。
まずは、探索するf(x)によって、関数の予測精度が大きく変わることを理解していただきます。
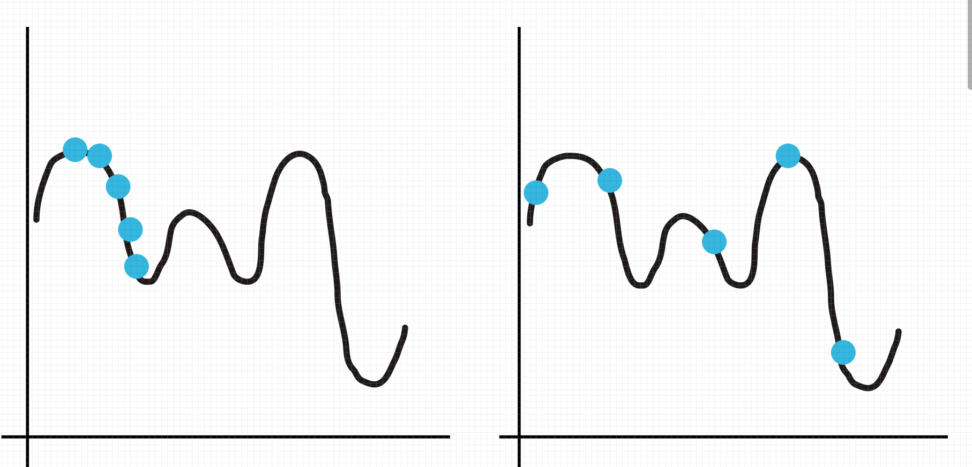
上の画像を見ていただければ、どのようなf(x)を観測した方が少ない探索回数で関数の形を理解しやすいかわかると思います。
左の探索方法では、左端部分の予測精度は高いですが、右側については全く未知です。
この「良さそうなf(x)の取り方」を決めるのが、ガウス過程回帰と獲得関数です。
ただコードが知りたいだけの方は、飛ばしていただいて構いません。
数学的背景|獲得関数(acquisition function)とガウス過程(Gaussian process)
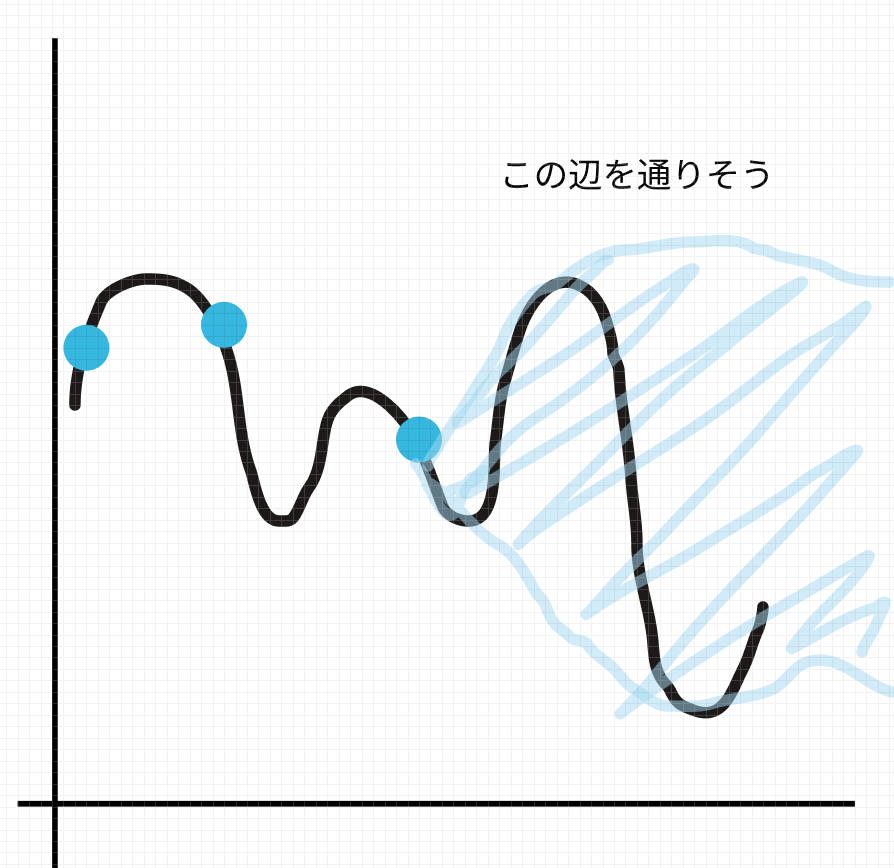
ガウス過程回帰は、探索したf(x)をもとに、関数がどのあたりを通りそうかという確率分布を予測として返します。(超大事)
こちらにガウス過程の詳しい解説を載せております。
【python】ガウス過程回帰の仕組みと実務での応用|ノンパラメトリック機械学習
また、観測データy_obが与えられた時のyの条件付き分布は、以下のように表されています。
ただし、KはK_ij=k(x_i,x_j)で定義されているn×nの行列です。
$$y|x~N(k(x)^TK_{ob}^{-1}y_{ob},k(x,x)-k(x)^T)K_{ob}^{-1}k(x)$$
$$k(x)=(k(x,x_1),…,k(x,x_n))^{T}$$
この分布は、ベイズ統計学では事後分布と呼ばれるものです。
\(y_{ob}\)を観測するごとに更新されていきます。
しかもガウス過程回帰のすごいところは、パラメータθの分布(これを事前分布と呼びます)を明示的に設定していなくても経験的に事後分布を作るというところです。
$$y = θx+ε$$
色々と複雑な話をしましたが、点xを与えたときのyの予測値の分布が多変量正規分布として求められているということです。
そもそもベイズ最適の目的とは、厳密には「関数の形を求めること」ではありません。
ゴールはゴールは関数の最小値を求めることです。
その上で、関数の形はできるだけ精緻に知っておいた方がいいよね、ということです。
パラメーターチューニングでいうと、「モデルパラメータxの時の検証誤差が最小になる最適なxを知りたい」ということになります。
ガウス過程回帰でyの分布を出した後に、獲得関数を使ってどのあたりのyの値をとったほうが決めるというフローになります。
$$min{\in{f(x)}}$$
さて、現在の探索までで得られているyの最小値を\(y_{min}\)で表すとします。
すると、\(y_{min}\)からどれだけ最小値を更新できるのかという期待値を表したものを期待改善量と呼び、獲得関数の一つとされています。
今回は、期待改善量を説明します。
$$a(x)=E[max(0,y_{min}-μ(x))]=(y_{min}-μ(x))\Phi(y_{min};μ(x),v(x))+v(x)\phi(y_{min};μ(x),v(x))$$
期待値なのでこちらの方が理解しやすいと思います。
\(μ(x),v(x)\):任意のxを得た時のyの推定値とその分散。
第1項:正規分布の分布関数の\(y_{min}\)における値と、\(y_{min}\)とxを与えた時の期待値の差の積
第2項:正規分布の確率密度関数の\(y_{min}\)における値と、分散の積
\(y_{min}\)が関数の中で小さければ小さいほど、xの候補が減ってくると理解できると思います。
期待改善量が最大になるxを探索しにいき、効率的に最小値を取れるように頑張るということです。
獲得関数には期待改善量以外にも下のように、平均予測値と分散を使った獲得関数もあります。
ただしこの獲得関数はβというパラメータを操作する必要があり、最適なパラメータを探索するために必要な獲得関数にもチューニングすべきパラメータがある、のでややこしいし、あまり使われません。
$$a_{LCB}(\boldsymbol{x})=μ(\boldsymbol{x})-βσ(\boldsymbol{x})$$
LCBというのは、lower confidence boundの略です。
予測平均が小さくなる場所を探索しても最小値が見つかりそうだし、分散が大きい部分を探索しても最小値が見つかりそう(周りの予測値は大きくてもブレがあるので)ですね。
ガウス過程に従っているので当然ですが予測値は平均ベクトル\(μ(\boldsymbol{x})\)、分散\(σ(\boldsymbol{x})\)のガウス分布に従っています。
ハイパーパラメータのチューニングには、他にもグリッドサーチやランダムサーチなどがあります。
詳しくは以下をご覧ください。
【XGB】GridSearchを使いつつ特徴量重要度を知りたいッ‥!|python
【XGB】交差検証法を使った勾配ブースティング決定木の実装|python
CODE
今回は、データ分析コンペのkaggleの登竜門とされる「titanic」のデータセットを使います。
・train.csv:教師データ
・test.csv:テストデータ
まずはデータの前処理を行い、その後にベイズ最適化を行い、機械学習に入ります。
1:前処理(feature engineering)
import numpy as np
import pandas as pd
from pandas import DataFrame, Series
import seaborn as sns
from sklearn.model_selection import train_test_split, KFold, cross_val_score, StratifiedKFold, validation_curve
from sklearn.ensemble import RandomForestRegressor
from xgboost import XGBRegressor
import matplotlib.pyplot as plt
import sklearn as skl
import optuna
from sklearn.metrics import roc_curve, auc
df = pd.read_csv("train.csv")
df_test = pd.read_csv("test.csv")必要なライブラリのインポートとデータの読み込みを行います。
ベイズ最適化のためのライブラリとして、optunaというものを使います。
簡単に実装ができる上、制限時間内での最適解を出力できるなどの便利な機能があります。
# 推定に使用する項目を抽出
age_df = df[['Age', 'Pclass','Sex','Parch','SibSp']]
# ラベル特徴量をワンホットエンコーディング
age_df=pd.get_dummies(age_df)]
# 学習データとテストデータに分離し、numpyに変換
known_age = age_df[age_df.Age.notnull()].values
unknown_age = age_df[age_df.Age.isnull()].values
# 学習データをX, yに分離
X = known_age[:, 1:]
y = known_age[:, 0]
# ランダムフォレストで推定モデルを構築
rfr = RandomForestRegressor(random_state=0, n_estimators=100, n_jobs=-1)
rfr.fit(X, y)
# 推定モデルを使って、テストデータのAgeを予測し、補完
predictedAges = rfr.predict(unknown_age[:, 1::])
df.loc[(df.Age.isnull()), 'Age'] = predictedAges Ageという特徴量には欠損値があります。
今回は、欠損値のない’Pclass’,’Sex’,’Parch’,’SibSp’を使ってランダムフォレストで予測値を算出して、欠損値を補完するという方法を取りました。
ランダムフォレストの詳しいアルゴリズムに関しては以下をご覧ください。
【ランダムフォレスト】ブートストラップ法を決定木に応用|python
テストデータに関しても同様の処理を行います。
# 推定に使用する項目を抽出
age_df_test = df_test[['Age', 'Pclass','Sex','Parch','SibSp']]
# ラベル特徴量をワンホットエンコーディング
age_df_test=pd.get_dummies(age_df_test)
# 学習データとテストデータに分離し、numpyに変換
known_age_test = age_df_test[age_df_test.Age.notnull()].values
unknown_age_test = age_df_test[age_df_test.Age.isnull()].values
# 学習データをX, yに分離
X = known_age_test[:, 1:]
y = known_age_test[:, 0]
# ランダムフォレストで推定モデルを構築
rfr = RandomForestRegressor(random_state=0, n_estimators=100, n_jobs=-1)
rfr.fit(X, y)
# 推定モデルを使って、テストデータのAgeを予測し、補完
predictedAges_test = rfr.predict(unknown_age_test[:, 1::])
df_test.loc[(df_test.Age.isnull()), 'Age'] = predictedAges_test
#cabinはほとんど欠損値なので削除する
df.drop('Cabin', axis=1, inplace=True)
df_test.drop('Cabin', axis=1, inplace=True)
sns.countplot('Embarked',data=df)
plt.title('Number of Passengers Boarded')
plt.show()cabinという特徴量に関しては、殆ど欠損値なので思い切って削除してしまいます。
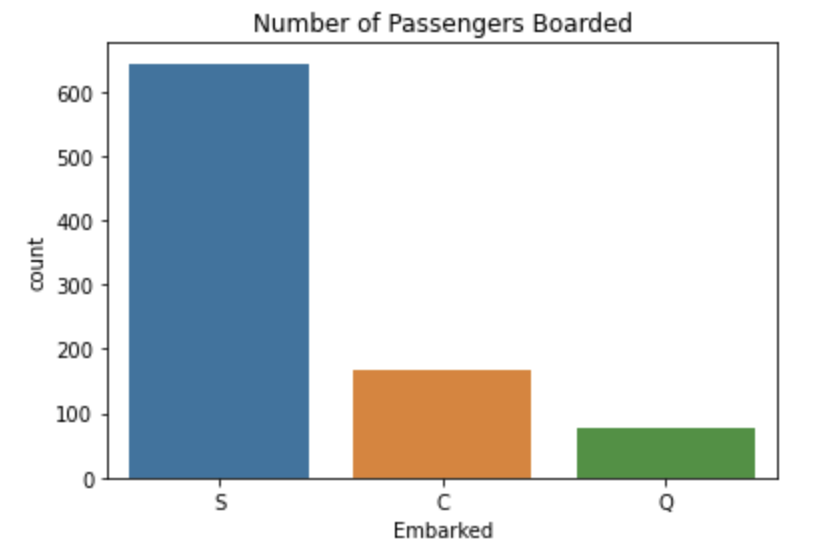
Embarkedというカテゴリカルデータに関しては、まずは分布を見てから判断します。
このように、大部分がSであることがわかります。
よって、欠損値はSで埋めることとします。
df['Embarked'].fillna('S', inplace=True)
df_test['Embarked'].fillna('S', inplace=True)
df_test.isnull().sum()→PassengerId 0
Pclass 0
Name 0
Sex 0
Age 0
SibSp 0
Parch 0
Ticket 0
Fare 1
Embarked 0
dtype: int64テストデータの欠損値を見ると、Fareに欠損値が一つあることがわかります。
これは、タイタニック号に乗るための料金です。
平均値で補完することとします。
#Fareは平均値を補完
df_test['Fare'].fillna('35.627188', inplace=True)
#NameやTikcetは削除
df.drop('Name', axis=1, inplace=True)
df_test.drop('Name', axis=1, inplace=True)
df.drop('Ticket', axis=1, inplace=True)
df_test.drop('Ticket', axis=1, inplace=True)NameやTicketに関しては、削除します。
Nameに関しては、MsやMrsなので年齢や家族構成を予測して欠損値を埋める処理が考えられます。
ぜひ挑戦してみてください。
#男性と女性は2値分類にする
df.replace({'Sex': {'male': 0, 'female': 1}}, inplace=True)
df_test.replace({'Sex': {'male': 0, 'female': 1}}, inplace=True)性別に関しては、2通りしかないので0,1に変換します。
下のように3分類以上あるEmbarkedは、ワンホットエンコーディング(one hot encoding)を行います。
Sを0、Cを1、Qを2などと設定すると誤った評価をしてしまうからです。
SとQの差は2なのに、SとCの差は1しかないという、カテゴリカルデータでは本来存在しなかった差が生まれてしまいます。
このため、ワンホットエンコーディングでは、要素の数だけ特徴量を作り、該当の特徴量だけ1を入力しています。
embarked = pd.concat([df['Embarked'], df_test['Embarked']])
embarked_ohe = pd.get_dummies(embarked)
embarked_ohe_train = embarked_ohe[:891]
embarked_ohe_test = embarked_ohe[891:]
df = pd.concat([df, embarked_ohe_train], axis=1)
df_test = pd.concat([df_test, embarked_ohe_test], axis=1)
#元のembarkedを消す
df.drop('Embarked', axis=1, inplace=True)
df_test.drop('Embarked', axis=1, inplace=True)*コンペによっては、教師データとテストデータの特徴量の分布が大きく異なる場合があります。注意しましょう。
2:パラメーターチューニング(parameter tuning)
先ほど取り上げたベイズ最適化を行います。
今回使うモデルは、GBDT(勾配ブースティング決定木アルゴリズム)のXGBです。
GBDTの詳細な説明は以下をご覧ください。
【XGB】交差検証法を使った勾配ブースティング決定木の実装|python
# 乱数シード
seed = 42
# チューニング前のモデル
model = XGBRegressor(booster='gbtree', objective='binary:logistic',
random_state=seed, n_estimators=100)
# 学習時fitパラメータ指定
fit_params = {'early_stopping_rounds': 10,
'eval_metric': 'logloss',
'eval_set': [(X, y)]
}
# クロスバリデーションして決定境界を可視化
cv = KFold(n_splits=10, shuffle=True, random_state=seed) # KFoldでクロスバリデーション分割指定チューニング前のモデルに関して、
n_estimators:学習する回数です。
→では、なぜこれは定数として設定していて、ベイズ最適化の対象に入れないかというと「意味がないからです」
n_estimators=1000の時点で、10や100を経験しており、わざわざ、n_estimators=10,100として区切る必要がないからです。
定石としては、n_estimators=10000のようにわざと大きめにとっておいて、early_stoppingを使うことです。
学習時のfitパラメータに関して、
early_stopping_rounds:学習時に評価指標として設定している値が、設定した回数だけ連続で改善しなくなった時点で学習をやめる
eval _metrics:early_sopping_roundsの評価指標です。2値分類問題なのでloglossを設定しています。
scoring = 'neg_mean_squared_error'
# ベイズ最適化時の評価指標算出メソッド
def bayes_objective(trial):
params = {
'learning_rate': trial.suggest_float('learning_rate', 0.01, 0.3, log=True),
'min_child_weight': trial.suggest_int('min_child_weight', 2, 8),
'max_depth': trial.suggest_int('max_depth', 1, 10),
'colsample_bytree': trial.suggest_float('colsample_bytree', 0.2, 1.0),
'subsample': trial.suggest_float('subsample', 0.2, 1.0),
'reg_alpha': trial.suggest_float('reg_alpha', 0.001, 0.1, log=True),
'reg_lambda': trial.suggest_float('reg_lambda', 0.001, 0.1, log=True),
'gamma': trial.suggest_float('gamma', 0.0001, 0.1, log=True)
}
# モデルにパラメータ適用
model.set_params(**params)
# cross_val_scoreでクロスバリデーション
scores = cross_val_score(model, X, y, cv=cv,
scoring=scoring, fit_params=fit_params, n_jobs=-1)
val = scores.mean()
return val
# ベイズ最適化を実行
study = optuna.create_study(direction='maximize',
sampler=optuna.samplers.TPESampler(seed=seed))
study.optimize(bayes_objective, n_trials=100)実装としては、関数を作って→実行というパターンです。
関数の中には、XGBで探索したいパラメーターの種類と範囲を加えておきます。
また、study.optimize(bayes_objective, n_trials=100)のn_trialsに関しては、探索回数のことです。
多ければ多いほど、処理に時間がかかります。
また、「n_trials=100の時に、時間がどれくらいかかるのか」と事前に知りたい場合がありますよね。
そんな方法はありませんので、例えば3分以内に最適な解を出してほしいという場合にはn_trialsではなくtimeoutを使いましょう。
study.optimize(bayes_objective, timeout=180)# 最適パラメータの表示と保持
best_params = study.best_trial.params
best_score = study.best_trial.value
print(f'最適パラメータ {best_params}\nスコア {best_score}')
→最適パラメータ {'learning_rate': 0.10316346044446496, 'min_child_weight': 4, 'max_depth': 8, 'colsample_bytree': 0.7004439463296043, 'subsample': 0.815334361981248, 'reg_alpha': 0.08602317024652126, 'reg_lambda': 0.08689223246655367, 'gamma': 0.003225305003064497}
スコア -0.12102113895277018最後に最適なパラメータを出力して、パラメータチューニングはおしまいです。
ここのスコアというのは、事前にscoringに設定した値になります。
3:機械学習(machine learning)
X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.3, random_state=42)
# 最適パラメータを学習器にセット
model.set_params(**best_params)
xgb_pred = model.fit(X_train,y_train)
y_pred_train = model.predict(X_train)
y_pred_valid = model.predict(X_valid)
fpr, tpr, thresholds = roc_curve(y_valid, y_pred_valid)
# AUCの算出
auc = auc(fpr, tpr)
# ROC曲線の描画
plt.plot(fpr, tpr, color='red', label='ROC curve (area = %.3f)' % auc)
plt.plot([0, 1], [0, 1], color='black', linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('Receiver operating characteristic')
plt.legend(loc="best")set_paramsを忘れないでください。
データを分割して学習させて、最後にX_testを入力データとして分割して予測値を出しましょう。
また、評価データに関してAUCを算出してみます。
AUCに関して、詳しく知りたい方は【多変量解析】ROC曲線とAUCによる判別分析|pythonをご覧ください。
下のように0.88(1に近いほど良い)でした。
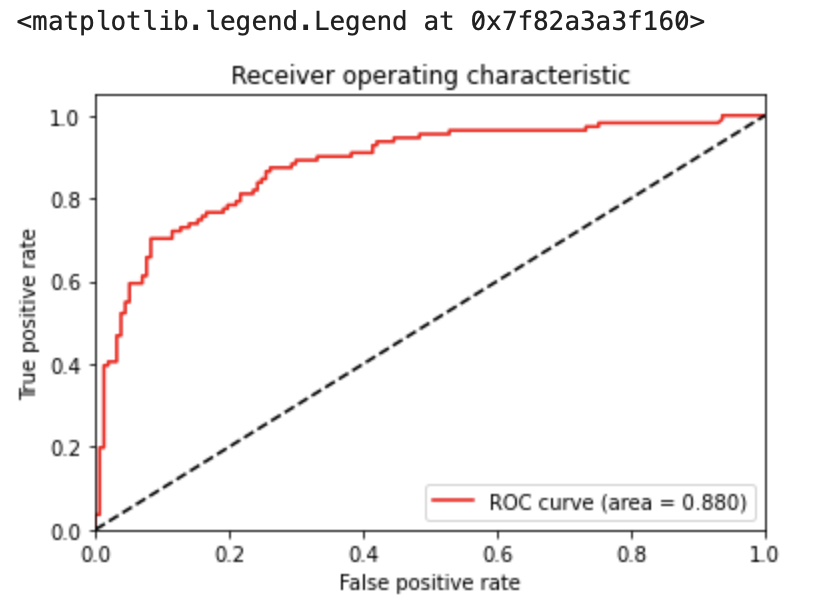
最後にX_testを入力して予測値を出します。
1になる確率が格納されているので、0.5を閾値にして2値分類します。
xgb_pred = model.predict(X_test)
#0と1にラベリング
xgb_pred = np.where(xgb_pred > 0.5, 1, 0)
xgb_pred[:5]→array([0, 0, 0, 0, 0])
他の機械学習コンテンツについては以下をご覧ください。
【Sequential】Kerasを使ったニューラルネットワーク|python
【ランダムフォレスト】ブートストラップ法を決定木に応用|python
【判別問題】サポートベクトルマシン(SVM)の仕組み|python
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


