【アンサンブル学習】ランダムフォレストをわかりやすく解説|ブートストラップ法を決定木に応用
こんにちは、青の統計学です。
今回は、決定木に対するバギングの拡張系アルゴリズムである「ランダムフォレスト(random forest)」を解説いたします。
前提知識|決定木
ランダムフォレストを理解するための第一歩は、その構成要素である決定木を知ることです。
決定木は、データを質問形式で分割していくことで、最終的な予測結果を導き出すモデルです。
例えば、「この顧客の年齢は30歳以上か?」、「過去の購入履歴は5回以上か?」といった質問を繰り返すことで、データを小さなグループに分けていきます。
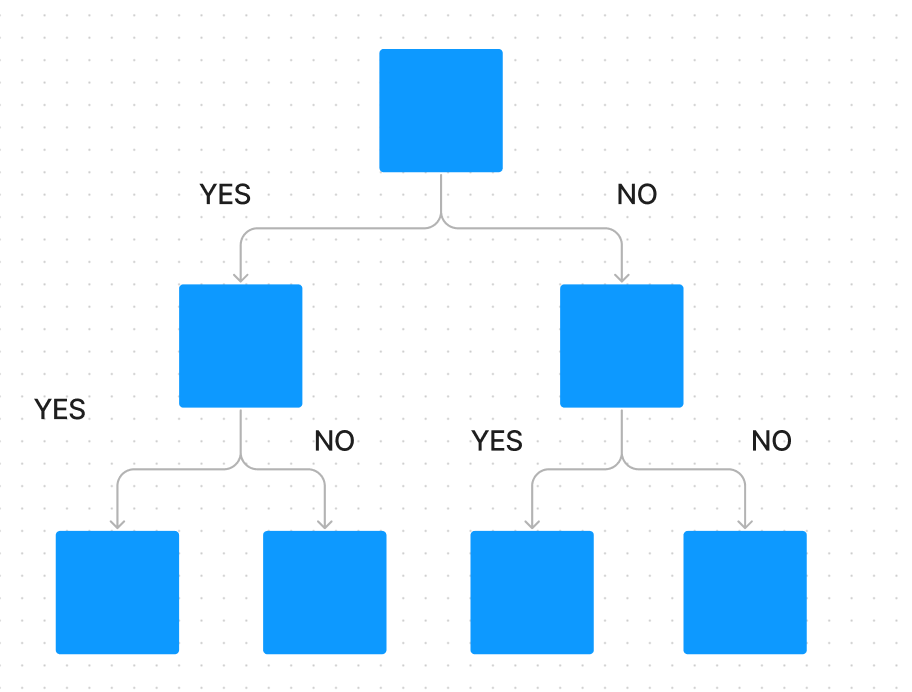
【機械学習】決定木の仕組みと数学的背景をわかりやすく解説|線形回帰との違い
分割の基準:不純度という概念
決定木がデータを分割する際、重要視するのが不純度(Impurity)です。不純度とは、あるノードに含まれるデータが、どれだけ混ざり合っているか(分類問題であれば、異なるクラスのデータがどれだけ混ざっているか)を示す指標です。
決定木は、分割によってこの不純度が最も大きく減少するような質問(特徴量と閾値)を選びます。分類問題でよく使われる不純度の指標には、ジニ不純度とエントロピーがあります。
ジニ不純度
そのノードからランダムに2つのサンプルを取り出したとき、それらが異なるクラスに属する確率を示します。
クラスの数を${K}$、クラス${k}$に属するサンプルの割合を${p_k}$とすると、ジニ不純度${G}$は次のように定義されます。
$$G = 1 – \sum_{k=1}^{K} p_k^2$$
${G}$が0に近いほど、そのノードは純粋(単一のクラスで構成されている)であることを意味します。
エントロピー
エントロピーは、情報理論における「情報の不確かさ」を表す指標です。
$$H = – \sum_{k=1}^{K} p_k \log_2(p_k)$$
決定木は、分割前後の不純度の差、すなわち情報利得が最大になるように分割を行います。
決定木の弱点:高いバリアンスと過学習
決定木は、データを完全に分類しようと深く成長させることができます。しかし、これが決定木の最大の弱点、過学習を引き起こします。
過学習とは、訓練データに対しては非常に高い精度を示すものの、未知の新しいデータに対しては精度が極端に落ちてしまう現象でした。決定木は、剪定がパラメータとしてあるものの、バリアンスが高くなりやすいです。
統計学で学ぶバイアス・バリアンス分解の考え方を思い出してください。モデルの予測誤差は、主にバイアス、バリアンス、そしてノイズの3つの要素に分解できます。
$$\text{Error} = \text{Bias}^2 + \text{Variance} + \text{Noise}$$
- バイアス
- モデルが単純すぎて、データの真の構造を捉えきれないことによる誤差(例:線形モデルで非線形なデータを予測しようとする)。
- バリアンス
- 訓練データが少し変わるだけで、モデルの予測結果が大きく変動してしまう不安定さ。
決定木は、深く成長させるとバイアスは低くなりますが、バリアンスが高くなります。

つまり、「木を見て森を見ず」の状態に陥り、個々の訓練データにこだわりすぎるあまり、全体的な傾向を見失ってしまうのです。
アンサンブル学習:バギングによるバリアンスの低減
アンサンブル学習とは、複数の「弱学習器」(ここでは決定木)を組み合わせることで、単一の学習器よりも優れた予測性能を持つ「強学習器」を構築する手法の総称です。ランダムフォレストは、アンサンブル学習の中でも特にバギング(Bagging: Bootstrap Aggregating)という手法をベースにしています。
ブートストラップサンプリングの数学的背景
バギングの核となるのが、ブートストラップ(Bootstrap)という手法です。ブートストラップは、母集団の分布が不明な場合に、手元の標本から「復元抽出」を繰り返すことで、疑似的な母集団を生成し、統計量の推定を行う手法です。
目的と合わせていうと、データのリサンプリング(復元抽出)を使って推定量の信頼区間を構成したり、バイアスの補正を行うための統計的な手法ですね。
ランダムフォレストでは、このブートストラップサンプリングを訓練データに対して行います。元の訓練データセット${D}$(サイズ${N}$)から、復元抽出によって${N}$個のサンプルを抽出した新しいデータセット${D_i}$を作成します。これを${T}$回繰り返すことで、${T}$個の異なる訓練データセット${D_1, D_2, \dots, D_T}$が生成されます。
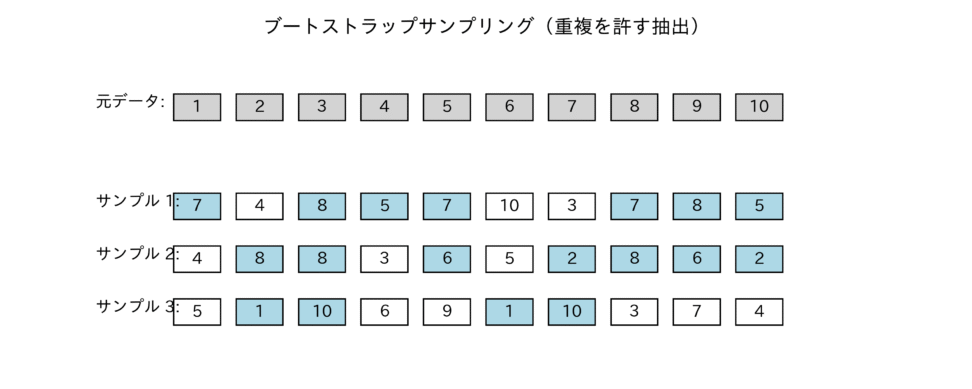
図は、ブートストラップサンプリングの概念図で、元のデータから復元抽出により複数のサンプルセットが生成され、各セットに重複や欠落があることがわかるかと思います。

この復元抽出により、各データセット${D_i}$は元のデータセット${D}$とは少しずつ異なる分布を持ちます。
バリアンスの低減:平均化による平滑化効果
バギングのアイデアはシンプルです。
- ブートストラップサンプリングで${T}$個の異なる訓練データセットを作成する。
- それぞれのデータセットで独立に決定木${h_i}$を訓練する。
- 最終的な予測は、すべての決定木の結果を平均(回帰)または多数決(分類)で集約する。
なぜこれでバリアンスが下がるのでしょうか?
ここで、大数の法則と中心極限定理の考え方が役立ちます。
${T}$個の独立した確率変数(ここでは決定木の予測結果)の平均を考えると、個々の予測結果のバリアンスが大きくても、それらを平均することで全体のバリアンスは小さくなります。
個々の決定木${h_i}$の予測誤差を${e_i}$、バリアンスを${V}$とします。もし、すべての決定木の予測誤差が完全に独立であれば、それらを平均したアンサンブルモデル${H}$のバリアンス${V_H}$は、
$$V_H = \frac{1}{T} V$$
となります。
つまり、決定木の数${T}$に反比例してバリアンスが減少するのです。

バギングは、個々の決定木が持つ「訓練データへの過度なこだわり」(高いバリアンス)を、多様な意見(?)の平均化によって打ち消し合い、より安定した予測結果(低いバリアンス)を得るための手法といえます
ランダムフォレストの独自性:特徴量のランダム選択
バギングだけでも決定木のバリアンスは改善されますが、ランダムフォレストはもう一歩踏み込みます。
それが、特徴量のランダム選択です。
バギングだけでは不十分な理由
もし、訓練データセット${D}$の中に、他の特徴量よりも予測能力の高い「強い特徴量」が一つ存在すると仮定します。
バギングによって生成された${T}$個のデータセット${D_i}$は、それぞれ異なるサンプルを含んでいますが、すべての${D_i}$は元のデータセット${D}$から派生しています。したがって、すべての決定木${h_i}$は、その「強い特徴量」を最も重要な分割基準として、木の根元(ルートノード)付近で利用する可能性が非常に高くなります。
結果として、すべての決定木${h_i}$は、その「強い特徴量」に依存した、似通った構造を持つことになります。

つまり、決定木間の予測結果に強い相関が生まれてしまうのです。
先ほどのバリアンスの式を思い出してください。
誤差が完全に独立(相関が0)であれば${V_H = V/T}$でしたが、実際には相関があります。決定木間の相関を${ \rho }$とすると、アンサンブルモデルのバリアンスは次のように近似されます。
$$V_H \approx \rho V + \frac{1-\rho}{T} V$$
この式からわかるように、決定木間の相関${ \rho }$が0でない限り、バリアンスは${T}$をどれだけ大きくしても${ \rho V }$より小さくはなりません。

つまり、相関が高いと、バギングの効果は頭打ちになってしまうのです。
特徴量サンプリングによる多様性の最大化
ランダムフォレストは、この相関の問題を解決するために、決定木を成長させる各ノードにおいて、特徴量のサブセットをランダムに選択し、その中から最適な分割特徴量を選ぶという制約を加えます。
- 分類問題: 全特徴量${M}$のうち、通常${ \sqrt{M} }$個の特徴量をランダムに選択します。
- 回帰問題: 全特徴量${M}$のうち、通常${ M/3 }$個の特徴量をランダムに選択します。
この制約により、「強い特徴量」がすべての決定木で使われる可能性が低くなります。結果として、個々の決定木は、異なる特徴量の組み合わせに基づいて成長し、予測結果の相関が低減されます。
ランダムフォレストの評価と解釈性
ランダムフォレストは、高い予測精度と安定性を誇るだけでなく、その評価と解釈性においても嬉しい特徴を持っています。
アウト・オブ・バッグ(OOB)誤差:交差検証なしでの評価
バギングのセクションで触れたように、ブートストラップサンプリングでは、元の訓練データの一部が各決定木の訓練に使われません。この使われなかったデータセットをアウト・オブ・バッグ(Out-Of-Bag: OOB)データと呼びます。
ランダムフォレストでは、このOOBデータを、その決定木が訓練に使わなかったサンプルに対するテストデータとして利用します。
1. あるサンプル${x_i}$が訓練に使われなかった決定木(OOB決定木)の集合を特定します。
2. そのOOB決定木群の予測結果を多数決(または平均)で集約し、${x_i}$の予測値とします。
3. この予測値と実際の値(正解ラベル)を比較し、誤差を計算します。
すべてのサンプルについてこの誤差を計算し、平均したものがOOB誤差です。

OOB誤差は、交差検証(Cross-Validation)を別途行うことなく、モデルの汎化性能を効率的かつ正確に推定できる、ランダムフォレストの大きな利点の一つですね
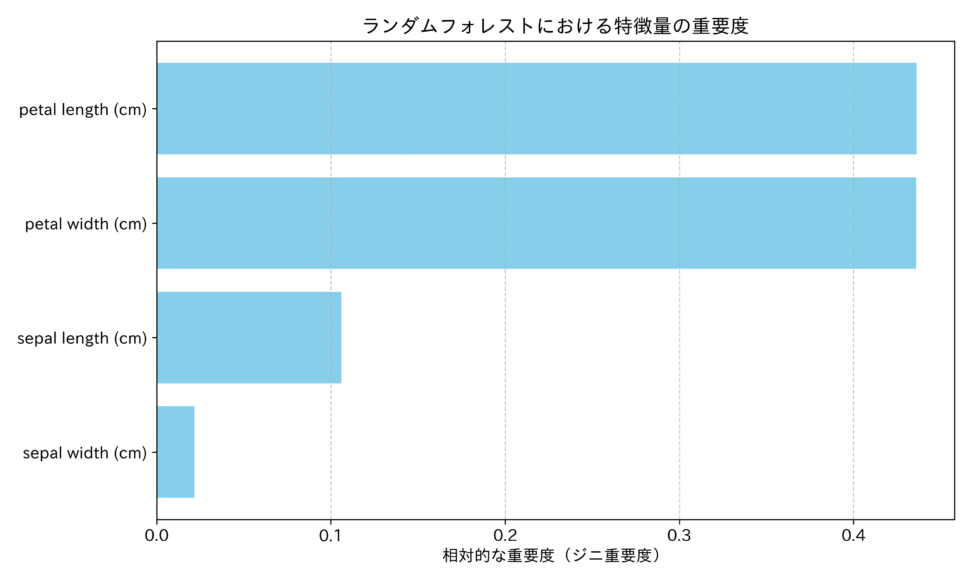
特徴量の重要度について
アンサンブル学習は、個々の決定木が複雑に絡み合うため、全体として「ブラックボックス」になりがちです。しかし、ランダムフォレストは、その構造から特徴量の重要度を算出できるという、解釈性を持っています。
最も一般的に用いられるのが、ジニ重要度(Gini Importance)、または平均不純度減少量(Mean Decrease in Impurity: MDI)に基づく方法です。
これは、ある特徴量が、すべての決定木を通じて、どれだけ不純度を減少させるのに貢献したかを平均して算出するものです。
- ある決定木において、特徴量${j}$が分割に使われたノードすべてについて、分割による不純度の減少量(情報利得)を計算します。
- すべての決定木について、この減少量を合計し、決定木の総数で割って平均します。
この値が大きいほど、その特徴量は予測において重要であると解釈されます。
というか、なぜ決定木を深くしても過学習しにくいのか
単一の決定木は、深く成長させると過学習します。しかし、ランダムフォレストを構成する個々の決定木は、通常、剪定(Pruning)を行わずに、可能な限り深く成長させます。
これは一見、過学習を助長するように見えますが、そうではありません。
1. 深い決定木はバイアスが低い: 完全に成長した決定木は、訓練データ内のすべてのパターンを捉えようとするため、モデルのバイアスは非常に低くなります。
2. バギングと特徴量サンプリングがバリアンスを吸収: 個々の決定木が持つ高いバリアンスは、バギングによる平均化と、特徴量サンプリングによる相関の低減によって、アンサンブル全体として効果的に打ち消されます。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!




