【python】Ridge(リッジ)回帰で多重共線性を解決する話
リッジ回帰とは、重回帰分析の一つであり、機械学習には厄介な「多重共線性」の影響を少なくできる手法のひとつです。
複雑なデータをモデルに当てはめるときには、一般に多くの説明変数を使って表現をしますが、
説明変数が増えるほど、説明変数同士での相関が生まれる危険があります。
今回は、単なる重回帰分析とリッジ回帰で多重共線性のあるデータに対する精度を比較してみます。
リッジ回帰(ridge regressor)
重回帰分析
$$Y_{i} = β_{0}+β_{1}X_{1}+β_{2}X_{2}+u_{i}$$
上の式は、重回帰分析の式の具体例です。
変数間の関数関係を記述するために、さまざまな統計モデルが提案されていますが、線形関係からなる線形回帰モデルはそれらの基礎になるものです。
説明変数が一つのものを単回帰、2つ以上のものを重回帰モデルと呼びます。
基本的な回帰分析については、こちらをどうぞ。
上図でいうβ0~β2などは回帰係数もしくは回帰パラメータと呼ばれます。
観測には、誤差uのズレを許しています。この観測誤差は、確率的に値を取ると考え、期待値0であると仮定します。
そして、分散と回帰係数は観測データから求めます。
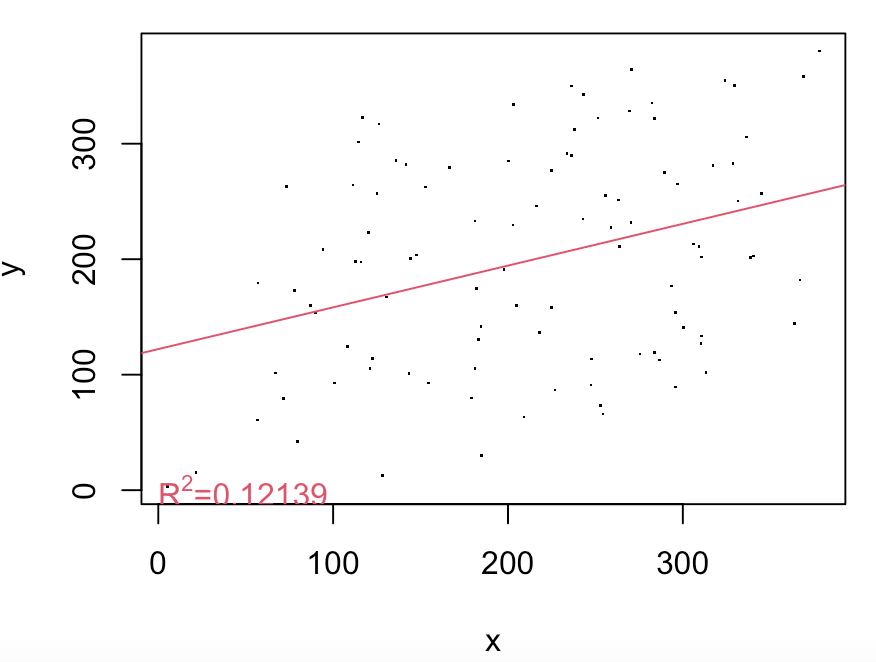
多重共線性
多重共線性とは、説明変数同士に強い相関があるということです。
説明変数同士に相関があるとなぜよくないのか。
→これに関しては、目的変数に対する重み(回帰係数)を計算する際に、相関が強いとどちらにどの程度重みをつけて良いかブレてしまうことになります。
なので、結局相関がある説明変数のうち、どちらが特徴量として重要なのかが学習のたびにブレてしまい、正しく特徴量重要度を評価できないというデメリットがあります。
相関が強いとはどの程度か、という問いに対しては、VIF(Variance Inflation Factor)などの定量的な指標があります。
詳しく理解したい方は、【説明変数の相関】多重共線性を解説します。をご覧くださいませ。
多重共線性の論文解説については、【論文解説】多重共線性は回帰分析にどのような影響を与えるのか
正則化と正則化項について(regularization)
さて、リッジ回帰は重回帰モデルの各回帰係数の算出時に正則化項というペナルティを設けています。
リッジ回帰における正則化項をL2ノルムと呼びます。
通常の重回帰分析では、予測値と実測値の差を表す損失関数(平均二乗誤差など)が最小になる各回帰係数の組み合わせを求めます。
しかし、リッジ回帰では、損失関数と正則化項の和が最小となる各回帰係数の組み合わせを求めるようにします。
L2ノルムは以下のように表します。
$$\sum_{I=1}^{N}β_{I}^2$$
L2ノルムとは、各回帰係数の2乗の和であることがわかりました。
最小二乗法にL2ノルムという制約を加えた最適化問題を考えます。
$$\sum_{I}(Y_{I}-f(X_{I}))^2$$
$$subject \quad to \sum_{l=1}^{L}β_{I}^2≦A$$
高校数学の知識を使えば、この制約が円の形をとるということに気づくと思います。
\(\sqrt{A}\)は円の半径ですね。\(A=0\)だと推定量はサンプル平均と一致し、\(A=∞\)だと最小二乗推定量に一致します。
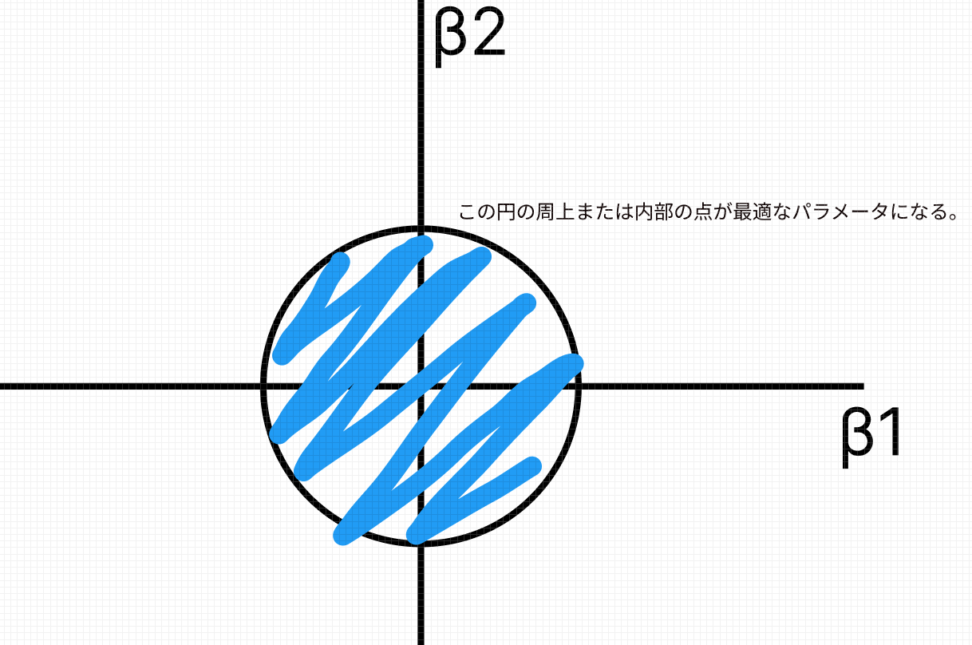
ラグランジュ未定乗数法を使って制約式を書き換えると以下のようになります。L2正則化項は第2項にあたります。
$$(y-β_{0}+β_{1}X_{1}+…+β_{n}X_{n})^2+α(\sum_{l=1}^Nβ_{l}^2)$$
こちらの式を図に表すと、以下のようになります。
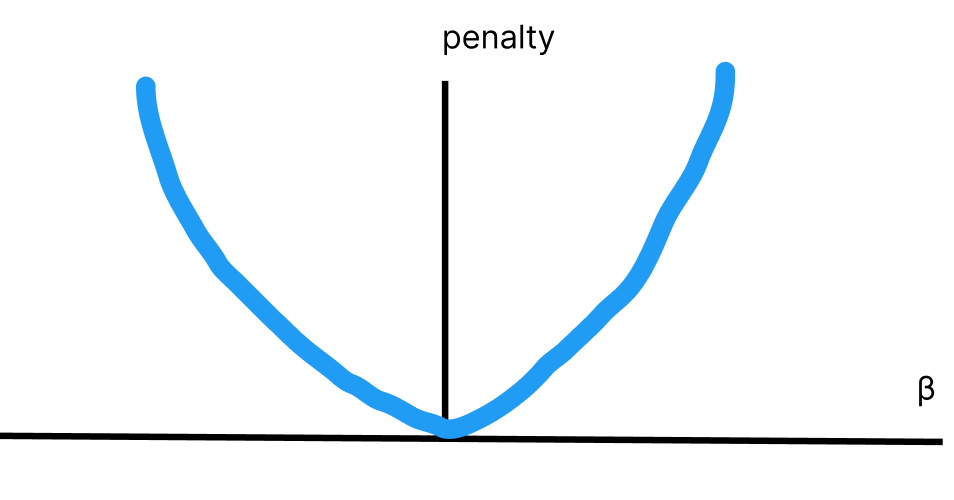
このように、損失を縦軸に取り、パラメータを横軸にとると二次関数の形をとります。
ご覧の通り、\(β=0\)の近傍では限界損失はほぼ0ですが、\(β\)が0から離れるほど、限界損失は大きくなります。
損失関数が小さくするパラメータが選択されると考えると、パラメータが0に近い値に収まるというのは納得できるはずです。
より一般化して、説明変数を\(β_iΦ(x_i)\)などのように関数化しても手順は変わりません。
この時の\(α\)を正則化パラメータと呼びます。そして、正則化パラメータの値が大きいと、線形回帰モデルの表現力が抑えられます。
正則化項を使う回帰の手法として、リッジ回帰とは別にラッソ回帰(正則化項はL1ノルムと呼ぶ)があります。
以下のような違いがあります。
ラッソ(Lasso)回帰:各説明変数の回帰係数を0に近づけつつ、特定の説明変数の回帰係数を0にするという特性
リッジ(Ridge)回帰:各説明変数の回帰係数を0に近づけるが、完全には0にしない。どの特徴量も大事なときに有効。
ラッソ回帰は次元削除に似た考えですね。
こうした正則化は、回帰係数が大きくなることで発生する過学習を防ぐ上でも有効です。
またラッソ回帰に関しては、説明変数が一つ減るので解釈のしやすさが高まります。
ラッソ回帰については、以下のコンテンツをご覧ください。
【python】Lasso(ラッソ)回帰で疎なデータに対応しよう|機械学習
正則化パラメーターの調整で、回帰係数にどんな変化が起きるのか
さて、正則化パラメーターαは基本的に0から1までの値で調整し、値が大きいほどペナルティが大きく、推定される回帰係数の値が小さくなります。
An Introduction to Statistical Learningでは、正則化パラメータの調整に関して以下のように解説しています。
正則化パラメータが0に近ければ近いほど、分散は大きくなり、バイアスは小さくなる。
→つまり、正則化の効果が薄い状態
正則化パラメータが大きいほど、分散は小さくなり、バイアスは大きくなる。
一般的に、正則化パラメータの上昇による分散の減少量は小さく、回帰係数の縮小により、回帰係数が過小評価され、バイアスの上昇幅としては大きくなります。
このような考えに基づくと、正則化を用いると比較的バイアスの上昇を最小限に抑えつつ、分散を大きく減らすことができる、データ数nに対して特徴量数pが大きい場合などに有用なことがわかります。
細かい話(bias-variance tradeoffとMallows’Cp基準)
一方で、正則化が強すぎると推定量が原点に向けて縮小され過ぎてしまい、予測精度がかえって悪くなることがあります。
これを過小適合(under fitting)と呼びます。
過学習(過適合)している場合は分散が大きく、過小適合している場合にはバイアスが大きいという「バイアス-バリアンス-トレードオフ」という言葉もあります。
平均二乗誤差(MSE)は、ノイズと分散の二乗とバイアスの和で表されることから、バイアスと分散がどちらかが大きすぎてもモデルとして望ましくないと言えます。
バイアスというのは「異なるデータセットで学習したモデルの平均化した出力と真の出力の差」のことです。
また、正則化項の係数はどのように決まるのでしょうか。
その基準としてMallows’Cp基準があります。
$$M(α)=Tr[X(X^TX+αI_{d})^{-1}X^T]$$
M(α)は統計的自由度です。転置行列が出てくるので少し難しいかもしれません。
そして、Mallow’sCp基準を用いたαの選択は、Cp(α)を最小化することで実現されます。
$$Cp(α)=||Y-X(\hat{β}_{R})||^2+2σ^2+M(α)$$
それほど難しい数式ではなく、第1項は平均二乗誤差です。
ちなみにマローズのCpは、ガウス線形回帰においては、赤池情報量基準と同じとされています。
CODE
scikitlearnの乳がんのデータを使って、リッジ回帰の精度を見てみましょう。
乳房塊の微細針吸引物(FNA)のデジタル化画像から計算されており、画像中に存在する細胞核の特徴を捉えたものです。
データセットの中では悪性(malignant)は0、良性(benign)は1で表されており、targetカラムで表されております。
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
import numpy as np
import pandas as pd
data_breast_cancer = load_breast_cancer()
# Pandasによるデータの表示
df_target = pd.DataFrame(data_breast_cancer["target"], columns=["target"])
df_data = pd.DataFrame(data_breast_cancer["data"], columns=data_breast_cancer["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
df.head()必要なライブラリをimportしてきて、乳がんデータをデータフレームの型にします。
ちなみにpandasのconcatメソッドは、データフレーム同士を結合することができます。
使い方としては、pd.concat([結合するDataFrame1,結合するDataFrame2],結合する方向)です。
結合する方向は、行の方向(縦)ならaxis=0で列の方向(横)ならaxis=1です。デフォルトはaxis=0なので、axis=0とわざわざ入力する必要はありません。
| target | mean radius | mean texture | mean perimeter | mean area | mean smoothness | mean compactness | mean concavity | mean concave points | mean symmetry | … | worst radius | worst texture | worst perimeter | worst area | worst smoothness | worst compactness | worst concavity | worst concave points | worst symmetry | worst fractal dimension | |
| 0 | 0 | 17.99 | 10.38 | 122.80 | 1001.0 | 0.11840 | 0.27760 | 0.3001 | 0.14710 | 0.2419 | … | 25.38 | 17.33 | 184.60 | 2019.0 | 0.1622 | 0.6656 | 0.7119 | 0.2654 | 0.4601 | 0.11890 |
| 1 | 0 | 20.57 | 17.77 | 132.90 | 1326.0 | 0.08474 | 0.07864 | 0.0869 | 0.07017 | 0.1812 | … | 24.99 | 23.41 | 158.80 | 1956.0 | 0.1238 | 0.1866 | 0.2416 | 0.1860 | 0.2750 | 0.08902 |
| 2 | 0 | 19.69 | 21.25 | 130.00 | 1203.0 | 0.10960 | 0.15990 | 0.1974 | 0.12790 | 0.2069 | … | 23.57 | 25.53 | 152.50 | 1709.0 | 0.1444 | 0.4245 | 0.4504 | 0.2430 | 0.3613 | 0.08758 |
| 3 | 0 | 11.42 | 20.38 | 77.58 | 386.1 | 0.14250 | 0.28390 | 0.2414 | 0.10520 | 0.2597 | … | 14.91 | 26.50 | 98.87 | 567.7 | 0.2098 | 0.8663 | 0.6869 | 0.2575 | 0.6638 | 0.17300 |
| 4 | 0 | 20.29 | 14.34 | 135.10 | 1297.0 | 0.10030 | 0.13280 | 0.1980 | 0.10430 | 0.1809 | … | 22.54 | 16.67 | 152.20 | 1575.0 | 0.1374 | 0.2050 | 0.4000 | 0.1625 | 0.2364 | 0.07678 |
次に相関行列とヒートマップを出して、特徴量がどの程度相関しているかを確認します。
corr_mat = df.corr(method='pearson')
corr_mat| target | mean radius | mean texture | mean perimeter | mean area | mean smoothness | mean compactness | mean concavity | mean concave points | mean symmetry | … | worst radius | worst texture | worst perimeter | worst area | worst smoothness | worst compactness | worst concavity | worst concave points | worst symmetry | worst fractal dimension | |
| target | 1.000000 | -0.730029 | -0.415185 | -0.742636 | -0.708984 | -0.358560 | -0.596534 | -0.696360 | -0.776614 | -0.330499 | … | -0.776454 | -0.456903 | -0.782914 | -0.733825 | -0.421465 | -0.590998 | -0.659610 | -0.793566 | -0.416294 | -0.323872 |
| mean radius | -0.730029 | 1.000000 | 0.323782 | 0.997855 | 0.987357 | 0.170581 | 0.506124 | 0.676764 | 0.822529 | 0.147741 | … | 0.969539 | 0.297008 | 0.965137 | 0.941082 | 0.119616 | 0.413463 | 0.526911 | 0.744214 | 0.163953 | 0.007066 |
| mean texture | -0.415185 | 0.323782 | 1.000000 | 0.329533 | 0.321086 | -0.023389 | 0.236702 | 0.302418 | 0.293464 | 0.071401 | … | 0.352573 | 0.912045 | 0.358040 | 0.343546 | 0.077503 | 0.277830 | 0.301025 | 0.295316 | 0.105008 | 0.119205 |
| mean perimeter | -0.742636 | 0.997855 | 0.329533 | 1.000000 | 0.986507 | 0.207278 | 0.556936 | 0.716136 | 0.850977 | 0.183027 | … | 0.969476 | 0.303038 | 0.970387 | 0.941550 | 0.150549 | 0.455774 | 0.563879 | 0.771241 | 0.189115 | 0.051019 |
| mean area | -0.708984 | 0.987357 | 0.321086 | 0.986507 | 1.000000 | 0.177028 | 0.498502 | 0.685983 | 0.823269 | 0.151293 | … | 0.962746 | 0.287489 | 0.959120 | 0.959213 | 0.123523 | 0.390410 | 0.512606 | 0.722017 | 0.143570 | 0.003738 |
一部抜粋しておりますが、上のような相関行列が出力されたと思います。
ただ、ぱっと見分かりにくいのでヒートマップを出力します。
import seaborn as sns
import matplotlib.pyplot as plt
plt.figure(figsize=(50,40))
sns.heatmap(corr_mat,
vmin=-1.0,
vmax=1.0,
center=0,
annot=True, # True:格子の中に値を表示
fmt='.1f',
xticklabels=corr_mat.columns.values,
yticklabels=corr_mat.columns.values
)
plt.show()
plt.figure(figsize=(50,40))は、図自体の大きさを変えます。ヒートマップの定義よりも前にしないと適用されません。
かなり相関がある特徴量が多そうですね。
次にデータセットを教師データとテストデータに分けます。
y = df["target"]
X = df.loc[:, "mean radius":]
# 訓練データとテストデータに分ける
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)次はロバストZスコアを使って正規化します。
ロバストZスコアは、平均のかわりに中央値(median)を、標準偏差の代わりに正規四分位範囲を用いた正規化です。
何が、頑健(robust)なのかというと、外れ値や異常値に強いという意味です。
平均や標準偏差は外れ値や異常値の影響を大きく受けるため、ロバストZスコアでは使われていません。
ロバストZスコアを算出する関数を作って、分割したデータを入れておきます。
#スケーリングの作業
#ロバストZスコアを採用
def robust_z(x):
from sklearn.preprocessing import robust_scale
from scipy.stats import norm
coefficient = norm.ppf(0.75)-norm.ppf(0.25)
robust_z_score = robust_scale(x)*coefficient
return robust_z_score
X_train_scaled = robust_z(X_train)
X_test_scaled = robust_z(X_test)
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train_scaled,y_train)上のようにインスタンスを作成して、fitすればリッジ回帰を行なってくれます。
y_train_pred = ridge.predict(X_train_scaled)
y_test_pred = ridge.predict(X_test_scaled)
print(y_train_pred[:5])
print(y_test_pred[:5])predict()で予測値を算出します。
→[ 0.86190545 -0.21636734 1.0858732 0.28284516 1.14223168]
[0.01625513 0.82522432 0.95466175 0.82238728 1.01006728]となりました。
手始めに5個だけデータを出してみました。
def get_eval_score(y_true,y_pred):
from sklearn.metrics import mean_absolute_error,mean_squared_error,r2_score
mae = mean_absolute_error(y_true,y_pred)
mse = mean_squared_error(y_true,y_pred)
rmse = np.sqrt(mse)
r2score = r2_score(y_true,y_pred)
print(f" MAE(平均絶対誤差) = {mae}")
print(f" MSE(平均二乗誤差) = {mse}")
print(f" RMSE(平均平方二乗誤差) = {rmse}")
print(f" R2Score(決定係数) = {r2score}")予測値を評価するためにいくつか指標を格納した関数を作っておきます。
mseは平均二乗誤差、r2_scoreは決定係数です。
【MSEを最小化】ガウス・マルコフの定理と最良線形不偏推定量について
指標がわからない方は、この辺を見ておくと良いかもしれません。
print("教師データスコア")
get_eval_score(y_train,y_train_pred)
print("テストデータスコア")
get_eval_score(y_test,y_test_pred)
→教師データスコア
MAE(平均絶対誤差) = 0.1710513424404963
MSE(平均二乗誤差) = 0.04782423453013554
RMSE(平均平方二乗誤差) = 0.21868752714806472
R2Score(決定係数) = 0.799129747421621
テストデータスコア
MAE(平均絶対誤差) = 0.22570692250497632
MSE(平均二乗誤差) = 0.08334050779715949
RMSE(平均平方二乗誤差) = 0.28868756086322717
R2Score(決定係数) = 0.6357440407972298
と出力されました。
リッジ回帰での予測とその評価値が出てきたので、次は単純な重回帰分析を行ってみます。
from sklearn.linear_model import LinearRegression
# 回帰モデルのインスタンス
model = LinearRegression()
# モデル学習
model.fit(X_train_scaled, y_train)
# 予測値(Train)
y_train_pred = model.predict(X_train_scaled)
# 予測値(Test)
y_test_pred = model.predict(X_test_scaled)リッジ回帰と同様に重回帰分析のモデルもインスタンスを作成し、fit→predictでおしまいです。
print("教師データスコア")
get_eval_score(y_train,y_train_pred)
print("テストデータスコア")
get_eval_score(y_test,y_test_pred)→教師データスコア
MAE(平均絶対誤差) = 0.1682376505800942
MSE(平均二乗誤差) = 0.046826082002163635
RMSE(平均平方二乗誤差) = 0.21639335018009134
R2Score(決定係数) = 0.8033221647676659
テストデータスコア
MAE(平均絶対誤差) = 0.25462592233149245
MSE(平均二乗誤差) = 0.11068579661621046
RMSE(平均平方二乗誤差) = 0.3326947499077953
R2Score(決定係数) = 0.5162261176199043
上のように教師データスコアとテストデータスコアが出ました。
テストデータスコアに関して、表にまとめてみましょう。
| リッジ回帰 | 重回帰 | |
| MAE | 0.22570692250497632 | 0.25462592233149245 |
| MSE | 0.08334050779715949 | 0.11068579661621046 |
| RMSE | 0.28868756086322717 | 0.3326947499077953 |
| R2 | 0.6357440407972298 | 0.5162261176199043 |
以上のようになりました。MAE(平均絶対誤差)、MSE(平均二乗誤差)、RMSE(平均平方二乗誤差)は損失関数なので小さい方が精度が高いです。
一方、決定係数は1に近い方が精度が高いです(ただし0.9以上ある場合は、過学習を疑ってください)。
ご覧のように評価指標によると、リッジ回帰の方が精度が高いと分かりました。
皆様もぜひ試してください。
Lasso回帰が良いのか、Ridge回帰が良いのか
前述した通り、リッジ回帰ではパラメータが小さくは抑えられますが、0にはなりません。
つまり、疎なデータ(sparce)では無駄な特徴量を省くことはできません。
一方でラッソ回帰では、パラメータが0になることは頻繁にあり、疎なデータには適切だと一般には言われています。
つまり、背景知識をもとに特徴量を選択したような密なデータ(dence)では、リッジ回帰の方が良いと考えられます。
遺伝子系や画像などの、スパースデータに関してはLasso回帰でいらない特徴量を減らした方が良いと考えられています。
画像などは特に、「この画像に写っているのは猫かどうか」を確かめるときに、背景の家などをうつした特徴量はいらないですね。
余談ですが、「この画像に映る動物は犬か猫か」という判定問題に対して、機械学習では背景が重要だと判断された話はあります。
例えば、犬を写した背景なら散歩中の草むらや屋外を写しがちですが、猫の写真の背景は基本的に家や布団、床などの屋内ですよね。
2乗項や交差項を大量に作成した場合も、ラッソが適しているかもしれません。
エラスティックネット(elastic net)とは
ラッソ回帰とリッジ回帰をバランスさせた損失関数を作る方法もあります。
これをエラスティックネットと呼びます。
以下のような損失関数を持ちます。
\(\sum_{I}(Y_{I}-f(X_{i}))^2+λ{\sum_{l}[α|β_{1}|+{\frac{1}{2}}(1-α)β_{l}^2]}\)
パラメータに絶対値をつけたラッソ回帰のペナルティとパラメータを二乗したリッジ回帰のパラメータがありますね。
他の教師あり学習モデルについては、以下をご覧ください。
【XGB】交差検証法を使った勾配ブースティング決定木の実装|python
【python】Ridge(リッジ)回帰で多重共線性を解決する話
【ランダムフォレスト】ブートストラップ法を決定木に応用|python
【判別問題】サポートベクトルマシン(SVM)の仕組み|python
【kaggle】ベイズ最適化とXGBでtitanicの予測問題を解く|python




