【MSEを最小化】ガウス・マルコフの定理と最良線形不偏推定量について
回帰分析等で算出した推定量を評価するとき、どのような指標があるでしょうか。
これまでは、一致性や不偏性を取り上げてきました。簡単に復習しましょう。
一致性(consistency):サンプル数を∞に近づけると、推定量はパラメータの真の値に確率収束する
不偏性(unbiasedness):推定量の期待値は、真の値に等しくなる。
もっと詳しく復習したい方は、【n-1】不偏分散を解説します。や【例題つき】固定効果推定と固定効果モデルについて解説|ランダム効果も添えてをご覧ください。
一致性と不偏性の詳しめの解説があります。
さて、今回は比較する推定量がどちらも一致性と不偏性を持っていた場合に使う指標をご紹介します。
それは、平均二乗誤差と呼ばれる指標です。
今回のコンテンツは、平均二乗誤差の解説をしつつ、それを最小化する最良線形不偏推定量(BLUE)についてご紹介します。
平均2乗誤差(mean squared error)
平均二乗誤差とは、簡単に言えば「ばらつきとバイアスの2乗の和」です。以下の式をご覧ください。
$$MSE(θ;\hat{θ})=E[(\hat{θ}(X)-θ)^2]$$
これは、推定量と真の値θの差の平方の期待値です。推定量誤差のことですね。
元々これは、母平均の近似式を推定しようと言うモチベーションから生まれた式であり、書き換えると\(min\sum_{i}(Y_{i}-f(x))^2\)のようになります。
\(Y_{i}\)は実現値です。
真に求めたいパラメータ\(β*\)は以下のように表すことができます。
$$β^*\in arg minE[(E[Y|X]-f(X))^2]$$
では、先ほどの式を少し展開してみます。
$$E[(\hat{θ}(X)-θ)^2] = E[((\hat{θ}-E[\hat{θ}])+(E[\hat{θ}]-θ))^2]$$
ちょっとトリッキーですが、推定量の期待値を足し引きしたもの(実質0)を間に加えてみます。
その後に展開して、項別に期待値をとりましょう。
$$E[(\hat{θ}-E[\hat{θ}])^2]+2E[(\hat{θ}-E[\hat{θ}])(E[\hat{θ}]-θ)]+E[(E[\hat{θ}]-θ)]$$
第1項から第3項まで詳しくみていきましょう。
第1項:推定量の分散。
偏差の二乗の期待値なので、分散になります。
第2項:0です。
偏差の期待値は0になるので、第2項は0になります。
第3項:バイアスの二乗
推定量の期待値からパラメーターを引いているので、バイアスです。
以上より、平均二乗誤差は以下のように表すことができます。
バイアスの二乗と分散の和ですね。
$$MSE(θ;\hat{θ})=Var(\hat{θ})+Bias(θ)^2$$
思い出していただきたいのは、不偏性は「バイアスがない」ということでした。
つまり、ある推定量が不偏性を持つ場合、平均二乗誤差の第2項は0になり、分散(ばらつき)と等しくなります。
$$MSE(θ;\hat{θ})=Var(\hat{θ})$$
平均二乗誤差は、機械学習で作成したモデルの予測精度を調べるための評価指標として利用されます。
主に回帰タスクで使われます。
または、最適なパラメーターを探索する時の評価指標としても使われます。
回帰分析について復習したい方は、以下のコンテンツをご覧ください。
bias variance tradeoff
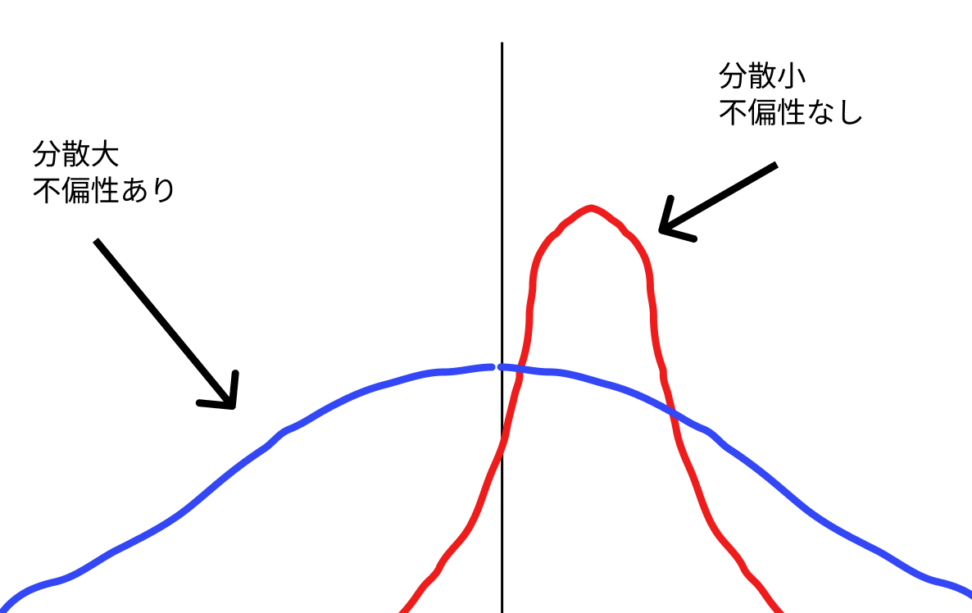
しばしば、「真の値の近くにばらつくことで、推定量の分散が小さいけれど、左右対称じゃない(不偏じゃない)」あるいは
「真の値に対して左右対称に分布(不偏)しているが、裾が広く、ばらつきが大きくなる」と言う問題が発生します。
下の図を見るとわかりやすいと思います。
青:不遍性あり、分散大
赤:不偏性なし(パラメーターを過剰に評価している)、分散小
黒:真の値
もっとわかりやすく言えば、下の的の図です。
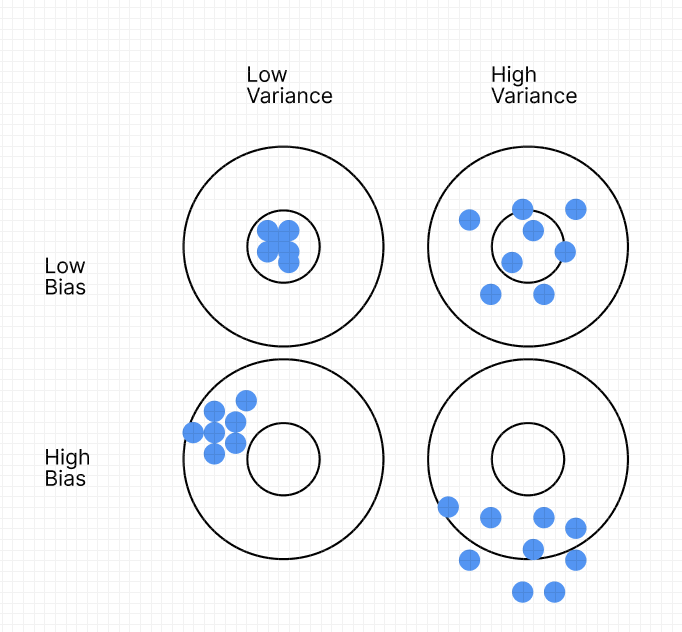
バイアスが大きくて、分散が大きい場合:平均しても的の中心にもないし、バラついている
バイアスが大きくて、分散が小さい場合:平均しても的の中心にもないが、ばらつきは少ない
バイアスが小さくて、分散が大きい場合:平均すると的の中心になりそうだが、ばらついている
バイアスが小さくて、分散が小さい場合:的の中心に点が集まっている
これをバイアスと分散のトレードオフ(bias variance tradeoff)と呼びます。
つまり推定量のバイアスが小さければ小さいほど良いというわけでも、ばらつきが小さければ小さいほど良いと言うわけでもないわけです。
このため、MSEは言うなれば「分散とバイアスの平均をとる」ことで、「すべてのθに関して、MSEが小さい方が推定量としては望ましい」という、妥当な指標になっているわけです。
CODE|python
ボストン住宅価格のデータを使って、平均二乗誤差を計算するコードを載せております。
モデルは線形回帰を使っています。
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# データの読み込み
boston = load_boston()
# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2)
# 線形回帰モデルの構築
reg = LinearRegression().fit(X_train, y_train)
# テストデータでの予測
y_pred = reg.predict(X_test)
# 平均二乗誤差 (MSE) の計算
mse = mean_squared_error(y_test, y_pred)
print("MSE:", mse)from sklearn.metrics import mean_squared_errorを使えば、簡単に出力することができます。
最良線形不偏推定量(BLUE)
推定量の中には、「線形推定量」と呼ばれるクラスがあります。
線形推定量というのは、下のようにそれぞれのデータを線形変換した推定量のことをいいます。
別に難しい話ではなく、例えば\(c_{i} =\frac{1}{n}\) なら、線形推定量は標本平均になります。
$$\hat{θ}= \sum_{i=0}^{N}c_{I}X_{i}$$
問題は、係数ciをどう決めたらよいかという話です。
まずは、不偏性を要求してみましょう。推定量の期待値が真の値と一致するという話でした。
$$E[\hat{θ}]=E[\sum_{i=0}^{N}c_{I}X_{I}]=\sum{i=0}^{N}c_{I}θ=θ$$
この時、ciの合計は1になる必要がありますね。(条件1)
$$\sum_{i=0}^{N}c_{i}=1$$
思い出してほしいのが、推定量が不偏性を満たす時には、「バイアスの2乗は0になる」のでMSEは推定量の分散に一致する、というものでした。
なので分散を求めてみましょう。
$$Var(\hat{θ})=E[(\hat{θ}-E[\hat{θ}])^2]=E[(\sum_{i=0})^{N}c_{I}(X_{I}-θ))^2]=\sum{i=0}^{N}c_{i}^2σ^2$$
上の式が分散です。これが、最小になればMSEを最小化した推定量だと言えます。
これを最良線形不偏推定量と呼びます。
発展:ラグランジュ未定乗数法
ここからは、「上の分散の最小値をどう求めるのか」までを知りたい方向けの話です。
最良線形不偏推定量が分かればokという方は、飛ばしてください。
方法としては、条件付きの最小化問題をラグランジュ未定乗数法を使って求めます。
条件としては、下のように不偏性を担保するために「変数の和が1」というものがありました。
$$\sum_{i=0}^{N}c_{i}=1$$
次に、上の章で求めた分散を見ます。iの添字がない母分散の方は、Σの外に出します。
$$σ^2 \sum_{i=0}^{N}c_{I}^2$$
σ^2は固定されているので、Σの中を最小化すれば良さそうです。
$$\sum{i=0}^{N}c_{I}^2-λ(\sum{i=0}^{N}c_{I}-1)の一階条件を解く$$
ラグランジュの未定乗数法とは、上のように「条件式を=0の形にした場合の左辺」をλに掛けて引きます(足しても良い)
次に、\(c_{i}\)と\(λ\)に関して一階微分します。
$$\frac{∂}{∂c_{i}}=2c_{i}-λ=0$$
$$\frac{∂}{∂c_{i}}=\sum_{i=0}^{N}c_{i}-1=0$$
この連立方程式を解いて終わりです。計算は省きます。
結局、最良線形不偏推定量は標本平均でした。
$$λ=\frac{2}{n},c_{i}=\frac{1}{n}より\hat{θ}=\sum_{i=0}^{N}c_{i}^2σ^2=\overline{x}$$
ラグランジュの未定乗数法は、数理最適化問題を解く上で頻繁に使われる手法の一つです。
ガウス・マルコフの定理
そして、「観測値を線型結合で表し、推定量を最小二乗法によって求めた場合の推定量は、最良線形不偏推定量になる」という定理を、ガウス・マルコフの定理と呼びます。
つまり、単回帰や重回帰などの線形モデルを最小二乗法で推定すれば、それはMSEを最小化できているというわけです。
回帰分析については、【機械学習】単回帰分析をpythonで実装してみましょうをご覧ください。
ガウス・マルコフの定理は統計検定準一級で出題範囲となっている定理です。この機会に覚えておきましょう。
損失関数について
今回紹介した平均二乗誤差は、シンプルな損失関数です。
損失関数は、別名コスト関数と呼ばれ、現在のモデルがどれくらい良いかを評価する関数です。
例えば、モデルが出鱈目な予測をすれば損失関数の値は大きくなり、逆に正確な予測をすればその値を予測すれば損失関数の値は小さくなります。
損失関数も同様に小さいほど良いモデルとされます。
クロスエントロピー
平均二乗誤差の他にもよく使われる損失関数は、クロスエントロピーというものがあります。
構成としては、正規の尤度関数に対数を追加したものになります。
$$-(ylogp+(1-y)log(1-p))$$
ラベルが0(y=0)の時に第1項が消え、ラベルが1(y=1)の時に第2項が消えます。
ラベル0の予測確率が1に近づくほど、またはラベル1の予測確率が0に近づくほど、クロスエントロピーの値が急上昇します。
正解データだと思っていたものを不正解データとして扱っていると、モデルとして致命的だよ(逆も然り)ということになります。
つまり、損失関数の値が高くなるので「よろしくないモデル」とみなされます。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!




