【線形代数】固有値や固有ベクトルは機械学習にどう使われているのか|主成分分析
こんにちは、青の統計学です。
今回は、前回大好評だった「線形代数がデータサイエンスにどう使われているのかシリーズ」の第二弾です。
大学数学で勉強した固有値や固有ベクトルが一体何の役に立っているのか…対角化で冪乗が簡単にできる以外に何が嬉しいのか…?
など、勉強した学問が実学としてどう活用されているのか知ると勉強する意欲が出ると思います。
線形代数を学びたい方はこちら
【python】行列式や逆行列は機械学習でどう使われるのか|線形代数の活用方法
【数理統計学】ヤコビアンをわかりやすく解説|MCMCでの使用例
統計検定のチートシートは以下をクリック！
【最短合格】統計検定準一級のチートシート|難易度や出題範囲について
【最短】統計検定2級合格ロードマップとチートシート|おすすめの本について
固有値(eigenvalue)と固有ベクトル(eigenvector)
固有値とは、正方行列に対して定義される特別な値で、行列を掛け算すると自分自身のスカラー倍になるベクトルが存在する場合にそれを求めることができます。
このようなベクトルを固有ベクトルといいます。
$$Aw=λw$$
上は正方行列に固有ベクトルをかけると、固有ベクトルのスカラー倍(ここではλ)になるという関係を表しています。
線形代数の分野ならった固有ベクトルと固有値はどのようにデータサイエンスに利用されているのでしょうか？
先に結論を述べておくと、固有値と固有ベクトルは「最適化問題が固有値問題に帰着できる」という文脈で登場します。
より具体的には、最適化問題が、ラグランジュ未定乗数法を使って制約条件を定式に加えて、一階条件をとると固有値問題(λが固有値)となります。
後述する主成分分析や線型判別問題に関しても、固有値が大きい順に固有ベクトルを選択します。
その1：主成分分析(primary component analysis)
主成分分析（PCA: Principal Component Analysis）は、高次元のデータをより低次元のデータに変換するための技術で、そのプロセスは固有値と固有ベクトルの概念に深く根ざしています。
主成分分析は、主に多重共線性を回避する場合や、特徴量が多すぎる場合に次元を削除するために、共分散行列の固有ベクトルを求め、主成分を上から取っていく手法です。
【論文解説】多重共線性は回帰分析にどのような影響を与えるのか
では、具体的な数学的背景を説明します。
元の説明変数を\(X_{1},X_{2},…,X_{k}\)とした時に、dをk以下の整数とした時に\(X_{1},X_{2},…,X_{k}\)の線型結合としてd個の新しい説明変数「主成分」を作ります。
$$Z_{k}=a_{1p}X_{1}+…+a_{kp}X_{k}\quad (p=1,…,d)$$
ただし制約として主成分の係数ベクトル\(a_{p}=(a_{1p},…,a_{kp})^T\)のノルムは1です。
$$||a_{p}||^2=\sum_{j=1}^{k}a_{jp}^2=1$$
次元削減の目的は、情報の損失を最小限に抑えながら、次元数を減らすことです。
ここで考慮すべきは、各説明変数xがk次元ベクトル空間内の点であるということです。
つまり、上の式で言うaをどう推定するのかが大事です。
ここで大事なのは、各説明変数xはk次元空間内の点です。
この時\((a \cdot x)a\)はベクトルaで貼られる部分空間への点xの直行射影に一致します。
(当然xは観測データ分だけ存在します)
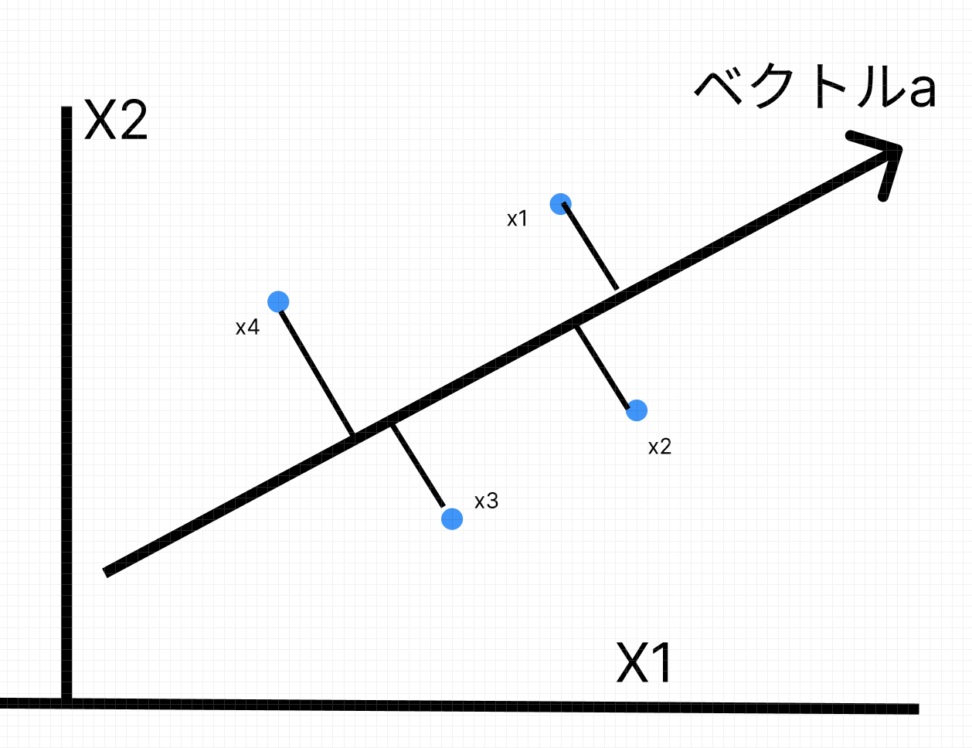
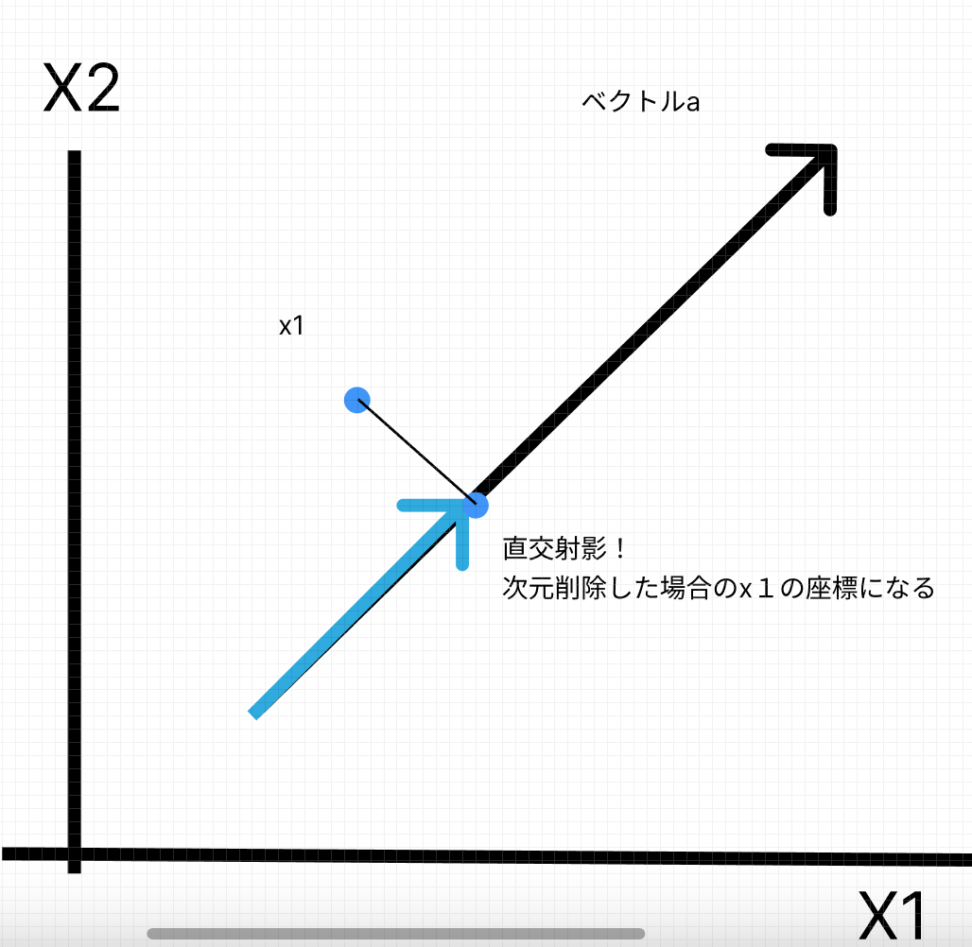
図示のために、観測データ4つと元の説明変数が2個の場合を想定しています。
ここでいうと\(a \cdot x_{1}\)はベクトル\(x_{1}\)のa方向の成分だとわかります。
以上のような幾何学的考察から、ベクトルaの適切な選び方としては、観測データのばらつきが最も大きい方向aを選ぶと言う方針になります。
つまり、以下のような制約付きの最適化問題を解くことになります。
$$\left\{\array{max \quad \sum_{i=1}^n(a \cdot x_{i}-a \cdot \overline{x})\\s.t \quad ||a||=1}\right.$$
共分散行列とは何か
主成分分析は特徴ベクトル\((x_{1},x_{2},…,x_{k})^T\)について合成変数\(Z_{k}=a_{1p}X_{1}+…+a_{kp}X_{k}\quad (p=1,…,d)\)の分散を最大化すれば良いという最適化問題になりました。
$$max V(Z)=max a^TXa$$
ここでラグランジュ未定乗数法とaによる一階微分により、以下のような固有値問題に落とし込めます。
Xは共分散行列でλは固有値、aは固有ベクトルです。
$$Xa = λa$$
求めるべき主成分の数だけこの固有値方程式を解き、最大の固有値に対応する固有ベクトルから順に選択します。
つまり、第一主成分の方向は最大の固有値に対応する固有ベクトル、第二主成分の方向は次に大きい固有値に対応する固有ベクトル、というように選択します。
これにより、元のデータの分散を最大限に保持しながら次元を削減することができます。
ではこの共分散行列とはなんでしょうか？
共分散行列は、データセットの特徴量間の関係性を捉えるための行列です。
特に、それぞれの特徴量がどのように共に変動するか、または互いにどの程度関連しているかを示します。
n次元のランダムベクトルXがあり、それぞれの成分がX1, X2, …, Xnであるとします。そのとき、共分散行列Σは次のようになります。
$$\sum =E[(X-μ)(X-μ)^T]$$
$$\begin{equation}\Sigma = \begin{bmatrix}\sigma_{1}^2 & \sigma_{12} & \cdots & \sigma_{1n} \\σ_{21} & \sigma_{2}^2 & \cdots & \sigma_{2n} \\vdots & \vdots & \ddots & \vdots \\σ_{n1} & \sigma_{n2} & \cdots & \sigma_{n}^2\end{bmatrix}\end{equation}$$
また共分散行列は以下の特性を持ちます。
対称性: 共分散行列は対称行列です。つまり、\(\sum_{i,j} = \sum_{j,i}が成り立ちます。
正定値性: 共分散行列は正定値または半正定値です。つまり、任意のベクトルvに対して、\(v^T\sum v >= 0\)が成り立ちます
つまり、固有値\(λ_j\)に対応する固有ベクトル\(a_{j}\)と元の特徴ベクトル\(x=(x_1,x_2,..,x_p)^T\)との内積を第j主成分と呼びます。
$$y_j = a_j \cdot x$$
共分散行列を固有ベクトルと固有値の行列で表現する固有値分解を行い、固有値が大きい順に固有ベクトルを選び出して、元のデータを固有ベクトルに射影することで、データの特徴を抽出することができます。
→元の共分散の情報量をできるだけ落とさずに次元を落とせた！！
まとめると、主成分分析による情報の集約と次元の削除のために、主成分の分散最大化と主成分間の無相関化を目指します。
そのために、特徴ベクトルの情報量が詰まった共分散行列を使って固有値と固有ベクトルを求めます。
→より正確には対称行列の直行行列の対角化の原理により実現する。
なぜなら、実数を要素とする対称行列は、その行列の固有値は実数であり、異なる固有値に対応する固有ベクトルたちは互いに直交(つまり無相関)するからです。
主成分分析について深く知りたい方は、以下のコンテンツをご覧ください。
【python】主成分分析(+回帰)の仕組みとコード例|教師なし学習
【共線性解決!?】pythonで主成分分析(PCA)をやってみた
その2：線型判別分析(liner discriminant analysis)
クラスタリングのタスクで使われる線型判別分析(LDA)にも固有値や固有ベクトルが使われます。
機械学習とデータサイエンスの世界では、LDAはクラスラベルを基にデータの特徴空間を最適化するための一つの手段として用いられます。
次元削減とクラス分離の目的で使用され、具体的な仕組みで言うと、クラス内の散らばり（within-class scatter）を最小化し、クラス間の散らばり（between-class scatter）を最大化することでデータを新たな特徴空間に射影します
数学的背景|線型判別分析
前述した通り、分類するクラス内の散らばりが小さいほど「良い判別基準」であり、分類するクラス間の散らばりが大きいほど「良い判別基準」である、と言うのはかなり直感的だと思います。
では、クラス内散布行列\(S_w\)とクラス間散布行列\(S_b\)を計算していきましょう。
クラス内分散
$$\begin{equation} S_W = \sum_{i=1}^{C} \sum_{x \in D_i} (x – m_i)(x – m_i)^T \end{equation}$$
クラス内分散は、各クラス内の共分散行列を足し合わせたものですね。
クラス間分散
$$\begin{equation}S_B = \sum_{i=1}^{C} N_i (m_i – m)(m_i – m)^T \end{equation}$$
クラス間分散は、各クラスの平均の共分散行列をクラスのデータの個数で重みをつけたものの和をとっています。
そして、クラス内分散を分母にとり、クラス間分散を分子にとります。
これをフィッシャーの判別基準と呼びます。
このJが最大になるような判別平面が目的に合致していると言えますね。
$$\begin{equation} J = \frac{|w^TS_Bw|}{|w^TS_Ww|},\end{equation}$$
「フィッシャー情報量」の方が有名かもしれません。
こちらは推定量の分散の下限を決定するクラメール・ラオの不等式に登場する、あるパラメータを変化させた時の確率分布の変化の度合いを表す情報量です。
【統計検定】フィッシャー情報量とクラメール・ラオの不等式について解説|python
さて、最適化問題を作ることができました。
この問題に制約条件は、分子が1になることです。今回2クラスで問題を扱うので求めるwは投影「ベクトル」です。
なぜかというと、定式の分母と分子がどちらもスカラーになるからです。
例えば投影ベクトルwの次元数をwとします。
すると、\( \frac{|w^TS_Bw|}{|w^TS_Ww|}\)は以下のような構造になっていることになります。
$$(1×D)(D×D)(D×1)→(1×1)$$
1×1なので当然スカラーです。
wを何倍しても定式の分母分子で打ち消し合うため、1という制約を置いている、というわけでございます。
$$\begin{equation} \max_{w} J(w) = \frac{w^TS_Bw}{w^TS_Ww} \quad s.t. \quad w^TS_Ww = 1 \end{equation}$$
線型判別分析での固有値と固有ベクトルの登場の仕方
さて、ラグランジュ未定乗数法を使って定式をいじってみます。
$$L = w^TS_{B}w-λ(w^TS_{w}w-1)$$
$$\frac{\partial L}{\partial w} = 2S_Bw-2λS_ww = 0$$
ここで一階条件で投影ベクトルwで微分してイコール0とします。
$$S^{-1}_{w}S_{B}w=λw$$
$$S_{B}=λS_W$$
固有値λ(最大固有値\(S_w^{-1}S_b\))で固有ベクトルがwの固有値問題に落とし込めました。
固有値に関しては、それが大きいほど、対応する固有ベクトルによる投影がクラス間の分散をより大きくし、クラス内の分散をより小さくします。
つまり、固有値はその固有ベクトルがどれだけ分類に効果的であるかを示す尺度となります。
したがって、通常は固有値が大きい順に固有ベクトルを選択します。
具体的には、最大の固有値に対応する固有ベクトルが最も分類に効果的な投影ベクトルとなります。
その次に大きな固有値に対応する固有ベクトルが2番目に効果的な投影ベクトルとなり、というように選択していきます。
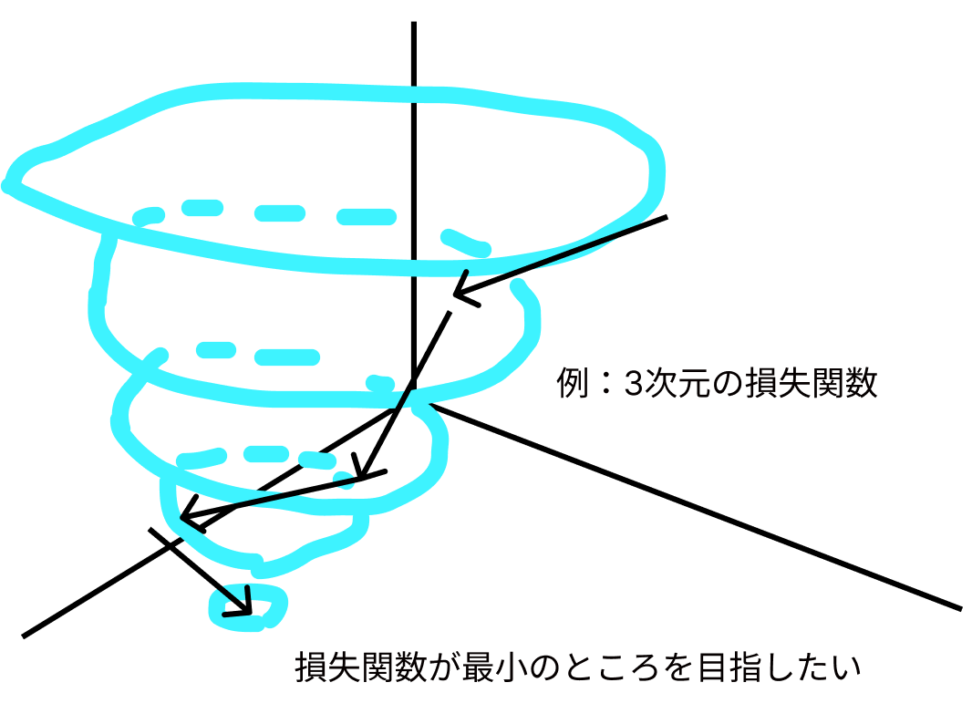
「解析的に解く」と「探索的に解く」…?
最適化問題を設けて、一発で答えを出そうとするのが前者であり、誤差を考慮しながら損失関数を小さくしていく営みが後者です。
今回お話ししたフィッシャーの判別基準を最大化するような超平面（具体的には投影ベクトル）を求めることが線型判別分析（LDA）の目的です。
ちなみに\(R^n\) において次元がちょうど 1 だけ小さい \(n − 1\) 次元 の空間のことを超平面 (hyperplane) といいます。
この最大化問題は解析的に解くことができます。
つまり、線形代数の問題に落とし込んで解けるよ、と言うわけです。
具体的には、$S_W^{-1}S_B$の固有ベクトルと固有値を計算します。最大の固有値に対応する固有ベクトルが最適な投影ベクトルとなります。
これは、クラス内分散を最小化し、クラス間分散を最大化する方向を探していると言えます。これは線形代数の問題として解くことができ、計算量も比較的少ないため効率的です。
なので、k-meansのように探索的に解を求めるようなイテラティブな手法を必要とせず、一度の計算で解を得ることができます。
【非階層型】K-means法でクラスタリングをしてみましょう。
ただ、こちらのコンテンツで取り上げた通り、特徴ベクトルが多重共線性の問題を抱えている(rank<n)と解析的に答えを出せないので、探索的なアルゴリズムを使いましょうとなります。
【python】行列式や逆行列は機械学習でどう使われるのか|線形代数の活用方法
今回は2次元ベクトル空間を例にとって超平面として直線を引くという最も理解しやすい場面を想定しましたが、多次元の場合でも最もよくデータを分離(→定義も同じくクラス内分散を小さく+クラス間分散を大きく)するような超平面をひくことになります。
線型判別分析を代表とする、判別タスクに対処する手法はいくらでもあります。
詳しくは以下のコンテンツをご覧ください。
【判別問題】サポートベクトルマシン(SVM)の仕組み|python
【python】カーネルSVMとは？kernel関数を利用した非線形データの判別問題に挑戦|機械学習
【多変量解析】ROC曲線とAUCによる判別分析|python
