主成分分析(PCA)をわかりやすく解説【統計検定準一級】|python
主成分分析
青の統計学へようこそ。
今回は、教師なし学習の一つ「主成分分析」について解説いたします。
数学的背景まで掘り下げたコンテンツは以下になります。
【python】主成分分析(+回帰)の仕組みとコード例|教師なし学習
多重共線性(multi colnierity)
多重共線性を解決する方法として、代表的な方法が2つあります。
①説明変数を除外する。これはダミー変数の罠に対応できました。
②主成分回帰を行う。
今回は②の主成分回帰の準備として、主成分分析について扱います。
主成分回帰は、多変量解析手法のうちで次元を削除する手法として代表的なものです。
相関のある多変量から、次元を下げて相関のない少数で全体のばらつきを表していく手法です。
多重共線性について復習しておきたい方は、以下のコンテンツをご覧ください。
【論文解説】多重共線性は回帰分析にどのような影響を与えるのか
少しだけ多重共線性の復習をしましょう。
多重共線性とは、説明変数同士が強い相関を持っているというものでした。
$$Y_{i}=β_{0}+β_{1}H_{i}+β_{2}C_{i}+u_{i}$$
上の例で言うと、HとCに相関があると言うことです。目的変数Yの上昇の原因が、HによるものなのかCによるものなのかが分からなくなってしまいます。
「多重共線性がないこと」は、重回帰モデルで最小二乗法を行う仮定のうちの1つでした。
母集団モデルを単回帰または重回帰モデルでかける 誤差項の平均は0(平均独立) 説明変数間に完全共線性がない 誤差項は互いに無相関 誤差項の分散は均一
主成分分析(principal component analytics)
主成分回帰は英語で略すとPCRです。
「多次元のデータを2,3次元に圧縮して、回帰分析をする」手法です。
多重共線性がモデルにあったときに、説明変数を削除したくないなら、主成分分析を行い、回帰する必要があります。
具体例を見てみましょう。
5人の中学生の定期テストの得点を集めました。 9個の科目の説明変数を使って、中学生の進路を判定するモデルを作ろうと思います。(今回はやらない) そのために、まずは主成分分析を行います。 以下の道具を使います。 データ:統計科学研究所の「成績のデータ」 言語:python ライブラリ:pandas,numpy,matplotlib,sklearn
主成分分析には、上で挙げた「scikit learn」が欠かせません。
sklearn.decomposion は、主成分分析を扱える分析器になります。
では、コードを解説していきます。
#各ライブラリの読み込み
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import sklearn
from sklearn.decomposition import PCA
#データの読み込み
seiseki = pd.read_csv('seiseki.csv')
seiseki.head()| kokugo | shakai | sugaku | rika | ongaku | bijutu | taiiku | gika | eigo | |
| 0 | 30 | 43 | 51 | 63 | 60 | 66 | 37 | 44 | 20 |
| 1 | 39 | 21 | 49 | 56 | 70 | 72 | 56 | 63 | 16 |
| 2 | 29 | 30 | 23 | 57 | 69 | 76 | 33 | 54 | 6 |
| 3 | 95 | 87 | 77 | 100 | 77 | 82 | 78 | 96 | 87 |
| 4 | 70 | 71 | 78 | 67 | 72 | 82 | 46 | 63 | 44 |
上のようになりました。今回は上のデータを主成分回帰しようと思います。まず、各要素を標準化しましょう。
1:行列の標準化
各列に対して、偏差を標準偏差で割ります。
# 行列の標準化
seiseki_s = seiseki.iloc[:, 0:].apply(lambda x: (x-x.mean())/x.std(), axis=0)
seiseki_s.head()| kokugo | shakai | sugaku | rika | ongaku | bijutu | taiiku | gika | eigo | |
| 0 | -1.022691 | 0.158349 | 0.222211 | 0.612592 | 0.771731 | 0.206080 | -0.780383 | -0.146861 | -0.646766 |
| 1 | -0.610524 | -0.866989 | 0.139690 | 0.285614 | 1.208511 | 0.555155 | -0.065504 | 0.696856 | -0.782325 |
| 2 | -1.068487 | -0.447533 | -0.933089 | 0.332325 | 1.164833 | 0.787871 | -0.930883 | 0.297200 | -1.121224 |
| 3 | 1.954064 | 2.209025 | 1.294990 | 2.340908 | 1.514256 | 1.136946 | 0.762250 | 2.162259 | 1.623855 |
| 4 | 0.809159 | 1.463325 | 1.336251 | 0.799437 | 1.295866 | 1.136946 | -0.441756 | 0.696856 | 0.166591 |
2:主成分分析の実行
主成分分析を行います。ここでは、pca = PCA() のように主成分分析を行うクラスのインスタンスを作っています。
どう主成分を抽出しているかというと、「分散が最大になる」ように主成分を選んでいます。
#主成分分析の実行
pca = PCA()
pca.fit(seiseki_s)3:作った主成分を主成分空間に写す
# データを主成分空間に写像
feature = pca.transform(seiseki_s)4:主成分得点を表示してみる
これによってPC1からPC8までの主成分が出来上がります。
for文を使って、列の数だけ主成分に名前をつけています。
# 主成分得点
pd.DataFrame(feature, columns=["PC{}".format(x + 1) for x in range(len(seiseki_s.columns))]).head()| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | PC9 | |
| 0 | 0.056415 | 0.916870 | -0.115763 | 1.188901 | 0.828176 | 0.096619 | -0.366566 | 0.271820 | -0.091322 |
| 1 | -0.147906 | -0.000470 | 0.659867 | 1.178344 | 1.236977 | 0.692963 | 0.438794 | -0.209384 | -0.060319 |
| 2 | 0.540050 | 0.542761 | 0.963296 | 1.847074 | 1.092440 | -0.048715 | -0.341034 | -0.500300 | 0.156104 |
| 3 | -5.107249 | 0.228059 | 0.625819 | -0.580088 | 0.292574 | -0.368834 | -0.301719 | 0.242537 | 0.313485 |
| 4 | -2.636544 | 0.661026 | 0.012114 | 0.879777 | 0.046665 | -0.464677 | 0.195361 | 0.287273 | -0.632364 |
この8個の主成分のうち、どこまで使えば良いでしょうか?
第一主成分と第二主成分でプロットしてみましょう。
5:第1主成分と第2主成分をプロットする
そもそも第三主成分以降は、plt.zlabel(“PC3”) のようにプロットできません。
「AttributeError: module ‘matplotlib.pyplot’ has no attribute ‘zlabel’」とエラーが出ます。
# 第一主成分と第二主成分でプロットする
plt.figure(figsize=(6, 6))
plt.scatter(feature[:, 0], feature[:, 1], alpha=0.8, c=list(seiseki.iloc[:, 0]))
plt.grid()
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.show()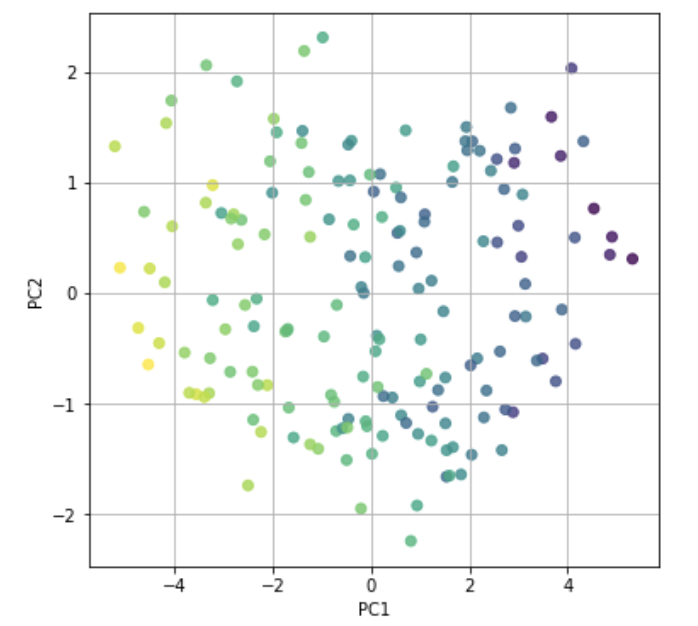
ギリギリですが、第1主成分と第2主成分で5人を区別できそうですね。
6:主成分で特徴を分けられるか作図
主成分を使って、特徴をとらえらるかを作図して把握します。
from pandas import plotting
plotting.scatter_matrix(pd.DataFrame(feature,
columns=["PC{}".format(x + 1) for x in range(len(seiseki_s.columns))]),
figsize=(8, 8), c=list(seiseki.iloc[:, 0]), alpha=0.5)
plt.show()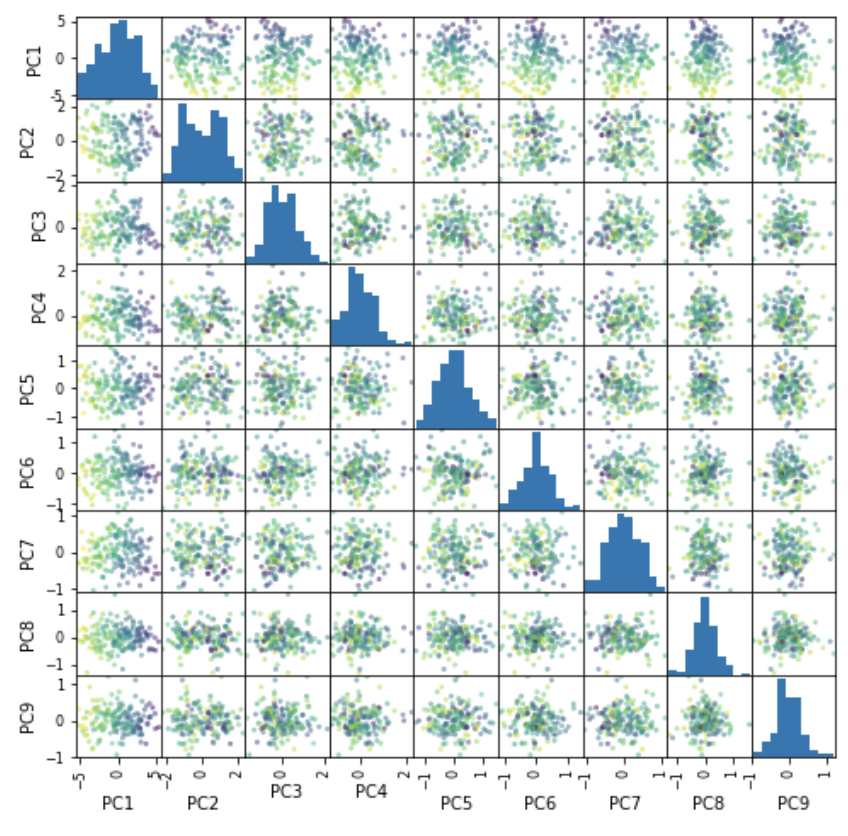
PC1の列とPC2の列が、色の区別ができています。特徴量の区別に関しては、第1主成分と第2主成分で十分だと言えます。
定性的に考えた後は、定量的に判断していきましょう。次は寄与率を見ます。
7:寄与率を求めよう
寄与率とは、主成分がどれくらいデータを説明できているかを表しています。一般的に1に近づくほど説明力が高いです。
決定係数の考え方に近いです。
累積寄与率は、作った主成分の寄与率の合計です。今回は9個の主成分を作ったので9個の主成分の合計は1です。
# 寄与率の計算
pd.DataFrame(pca.explained_variance_ratio_, index=["PC{}".format(x + 1) for x in range(len(seiseki_s.columns))])| 0 | |
| PC1 | 0.667381 |
| PC2 | 0.122021 |
| PC3 | 0.054538 |
| PC4 | 0.045220 |
| PC5 | 0.033362 |
| PC6 | 0.024607 |
| PC7 | 0.020310 |
| PC8 | 0.019022 |
| PC9 | 0.01354 |
# 累積寄与率を図示する
import matplotlib.ticker as ticker
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0] + list( np.cumsum(pca.explained_variance_ratio_)), "-o")
plt.xlabel("Number of principal components")
plt.ylabel("Cumulative contribution rate")
plt.grid()
plt.show()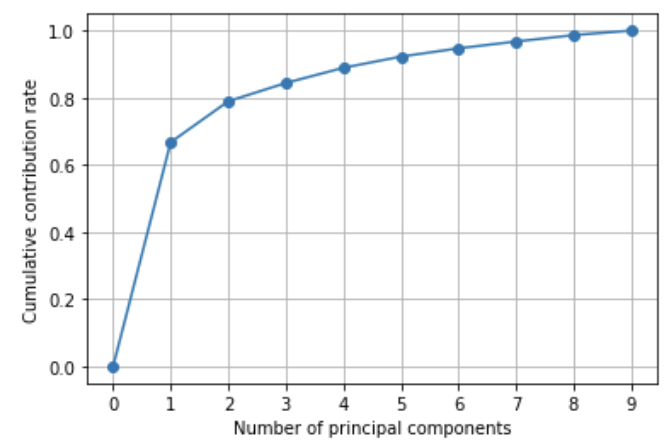
累積寄与率を見ると、第1主成分と第2主成分で大体データを説明できるとわかりました。
最後は、固有のベクトルを求めてみましょう。
8:固有ベクトルを求める
説明の前に一旦コードを見てみましょう。
# PCA の固有値
#固有値ベクトル
pd.DataFrame(pca.explained_variance_, index=["PC{}".format(x + 1) for x in range(len(seiseki_s.columns))])| 0 | |
| PC1 | 6.006431 |
| PC2 | 1.098185 |
| PC3 | 0.490842 |
| PC4 | 0.406976 |
| PC5 | 0.300260 |
| PC6 | 0.221459 |
| PC7 | 0.182787 |
| PC8 | 0.171195 |
| PC9 | 0.121864 |
主成分ごとの固有値を求めました。次に固有ベクトルを求めます
# PCA の固有ベクトル
pd.DataFrame(pca.components_, columns=seiseki.columns[:], index=["PC{}".format(x + 1) for x in range(len(seiseki_s.columns))])| kokugo | shakai | sugaku | rika | ongaku | bijutu | taiiku | gika | eigo | |
| PC1 | -0.362639 | -0.368570 | -0.356895 | -0.367226 | -0.354309 | -0.312678 | -0.139248 | -0.316726 | -0.356949 |
| PC2 | -0.149422 | 0.147029 | 0.181437 | 0.250686 | -0.009508 | -0.312168 | -0.859298 | 0.148958 | 0.046610 |
| PC3 | 0.073623 | -0.061551 | -0.399680 | 0.008251 | -0.199606 | 0.263783 | -0.080264 | 0.783869 | -0.317273 |
| PC4 | -0.236443 | -0.106524 | 0.029476 | 0.066644 | 0.356880 | 0.712269 | -0.284248 | -0.293357 | -0.354812 |
| PC5 | -0.301468 | -0.086651 | -0.061124 | 0.262381 | 0.642392 | -0.440125 | 0.268566 | 0.189814 | -0.338372 |
| PC6 | -0.494063 | -0.572745 | 0.408150 | 0.038858 | -0.131948 | 0.136309 | 0.106634 | 0.286649 | 0.360888 |
| PC7 | 0.619991 | -0.516987 | 0.408898 | -0.176506 | 0.119437 | -0.124784 | -0.127556 | 0.041500 | -0.319615 |
| PC8 | -0.109703 | 0.234943 | 0.446183 | 0.392465 | -0.495133 | -0.001600 | 0.234850 | -0.061830 | -0.524902 |
| PC9 | 0.231160 | -0.411562 | -0.377484 | 0.736380 | -0.132927 | 0.003495 | -0.007348 | -0.230749 | 0.146459 |
固有値と固有ベクトルについて
主成分分析を深く理解するには線形代数の知識が欠かせません。
行列は掛け合わせるもので、ベクトルを別のベクトルに変えることができますがここでは、方向を変えないベクトルを求めます。
これを固有ベクトルと呼びます。
そしてそのスカラー倍率のことを固有値と呼びます。
$$Ax=λx$$
あるn次正方行列Aに対して上のような関係を満たすn次元ベクトルx(0ベクトルではない)を固有ベクトルと呼び、λをxに対する固有値と呼びます。
理解していただきたいことは、PC1やPC2を説明する係数に相当するということです。
$$PC1=-0.362639(kokugo)-0.368570(shakai)+…$$
PC1とPC2で説明変数を作れたら、次元が9(元々の科目数)から2(主成分数)になると言うことです。
これが、主成分分析のメリットです。
つまり固有値が出た理由としては、具体的には正方行列を固有ベクトルと固有値の行列で表現する固有値分解を行い、固有値が大きい順に固有ベクトルを選び出して、元のデータを固有ベクトルに射影することで、データの特徴を抽出することができます。
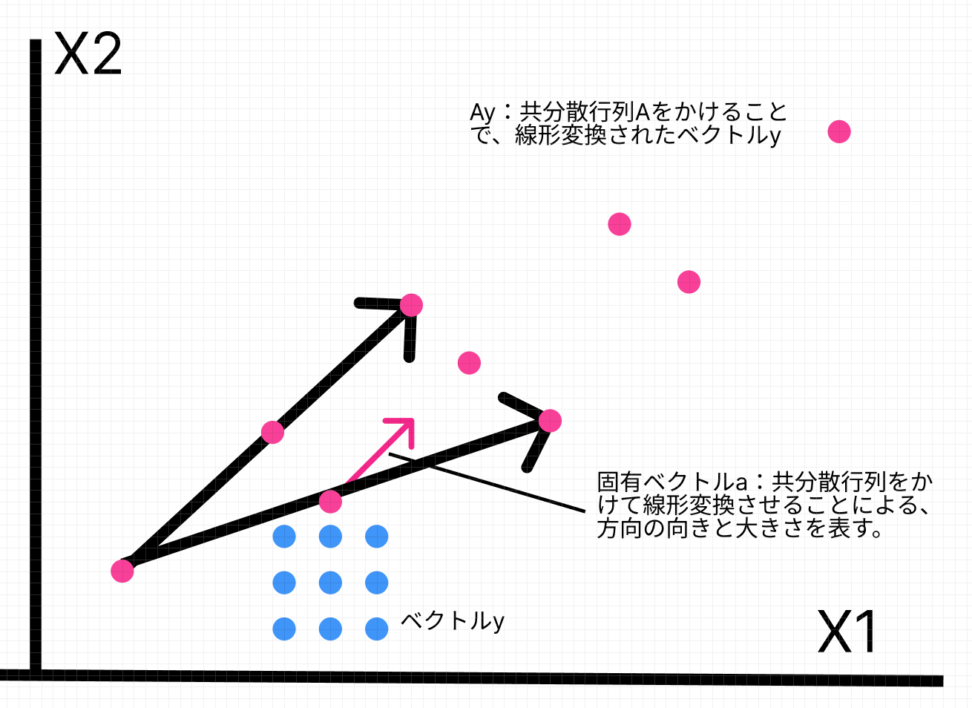
ここの正方行列というのは、基本的には分散共分散行列であり特徴量ベクトルの散らばり具合、つまり情報量を格納した正方行列です。
$$\pmatrix{ V(X_1)&COV(X_1,X_2)&…&COV(X_1,X_n) \\ COV(X_2,X_1)&V(X_2)&…&COV(X_n,X_1) \\ COV(X_n,X_1)&COV(X_n,X_2)&…&V(X_n)}$$
主成分分析では、このように正方行列を固有ベクトルと固有値に分解することによって、元のデータを低次元で表現することができます。
ちなみに先ほどの寄与率は、各主成分の固有値を足し合わせて割合をとったものです。最後の工程では、これを使います。
10:観測変数の寄与度をプロットする
実際PC1とPC2は、なにを表すのでしょうか。実際に主成分回帰を行う時に、説明変数となる主成分等が「何を表すのか」わかっていないと、結論が出しづらいですね。
そのために、元の説明変数(ここでは9個の科目)をどれくらい説明できているのかを寄与率の視点から見てみましょう。
# 第一主成分と第二主成分における観測変数の寄与度をプロットする
plt.figure(figsize=(6, 6))
for x, y, name in zip(pca.components_[0], pca.components_[1], seiseki.columns[1:]):
plt.text(x, y, name)
plt.scatter(pca.components_[0], pca.components_[1], alpha=0.8)
plt.grid()
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.show()

PC1:基本負であり、gika(技科でしょうか)の重みが少ない。
PC2:技科を負に評価している。音楽や理科、数学を高く評価している。
「文系を評価できている主成分」と「理系を評価できている主成分」に分けられると、「理系の科目の点数が高いと‥」のような雑なことを言えたのですが、全然そんな結果にはなりませんでした。
技術の能力と、それ以外の科目の能力は相関が少ないと言うことでしょうか。それはそれで興味深いです。
せっかくなので主成分回帰の話をすると、今の主成分たち(多くて3つ)を使って重回帰分析を行うだけです。
主成分を説明変数に使っているので、多重共線性の問題はありません。
以下のモデルを見ると、各主成分がどんな意味を持つのか知る必要があるとわかっていただけたでしょうか。
$$Y_{i}=dPC1+ePC2$$
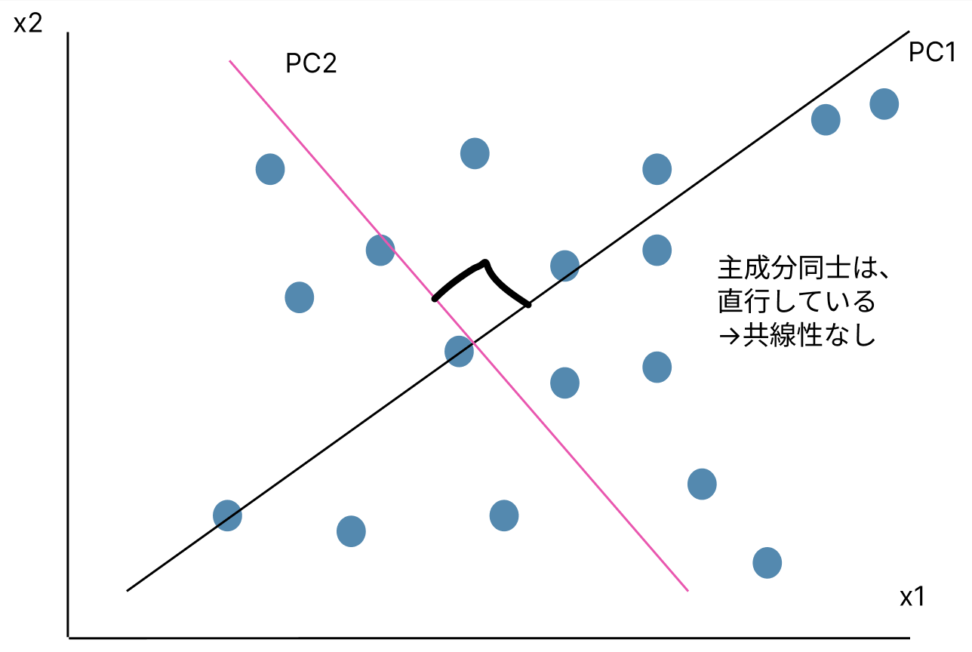
主成分同士には共線性はないのか
主成分同士は、多重共線性はありません。それぞれが直行し合うので、相関はありません。
嬉しいこと
最後に主成分分析のメリットを列挙します。
1:多重共線性を回避できる
2:多次元から2、3次元にすることでデータを視覚化する
例えば、50変量もあると複雑すぎて人間には理解できないですね。基本3次元以下のグラフにしないと人間は理解が困難です。
3:計算負荷を下げる
主成分回帰とは、主成分分析と重回帰分析が混ざったものです。
これまで色々な手法を見てきましたが、基本は基礎的な手法を組み合わせて、難しい状況(欠損データ/多重共線性/交絡因子/自己相関など)に対応できるような手法を作っているだけです。
例えば、以下のコンテンツなどです。
【交絡を解決!?】共分散分析(ANCOVA)とは一体何なのか。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


