【python】主成分分析(+回帰)の仕組みとコード例|教師なし学習
こんにちは、青の統計学です。
今回は教師なし学習の一つ「主成分分析」について解説いたします。
以下の記事よりも数学的背景を重めに取り扱っております。
【共線性解決!?】pythonで主成分分析(PCA)をやってみた
主成分分析(principal component analysis)
主成分分析（PCA）は、多変量解析の一種であり、多次元のデータを低次元のデータに圧縮する手法です。
主成分分析を使うことで、複数の変数間に相関関係がある場合、変数間の情報を簡潔にまとめることができます。
またこの手法は、データを構成する変数のうち、相関が強いものをグループ化して、新たな変数を作り出すことで、元のデータよりも情報量を減らしながらも、その変数が持つ情報をできるだけ多く保持することができます。
→これをこの工程を次元削除と呼びます。
主成分分析は線形な次元削減方法の一つです。
主成分分析の結果得られた変数は、元の変数とは異なる形式で表現されるため、解釈が難しいことがありますが、その分、多数の変数を一度に扱う際に有用な手法です。
数学的背景
ざっくり言えば、主成分分析とは「共分散行列の固有ベクトルを求める」ことです。
詳しく掘り下げていきます。
先ほど主成分分析とは「次元削除」と説明しましたが、数式で表すと以下のようになります。
元の説明変数を\(X_{1},X_{2},…,X_{k}\)とした時に、dをk以下の整数とした時に\(X_{1},X_{2},…,X_{k}\)の線型結合としてd個の新しい説明変数「主成分」を作ります。
$$Z_{k}=a_{1p}X_{1}+…+a_{kp}X_{k}\quad (p=1,…,d)$$
ただし制約として主成分の共変量\(a_{p}=(a_{1p},…,a_{kp})^T\)の長さは1です。
$$||a_{p}||^2=\sum_{j=1}^{k}a_{jp}^2=1$$
さて、次元削除なので当然\(d<k\)です。
元々の説明変数の情報量(データのばらつき)をできるだけ落とさずに、主成分を作りたいものです。
つまり、上の式で言うaをどう推定するのかが大事です。
ここで大事なのは、各説明変数xはk次元空間内の点です。
この時\((a・x)a\)はベクトルaで貼られる部分空間への点xの直行射影に一致します。
(当然xは観測データ分だけ存在します)
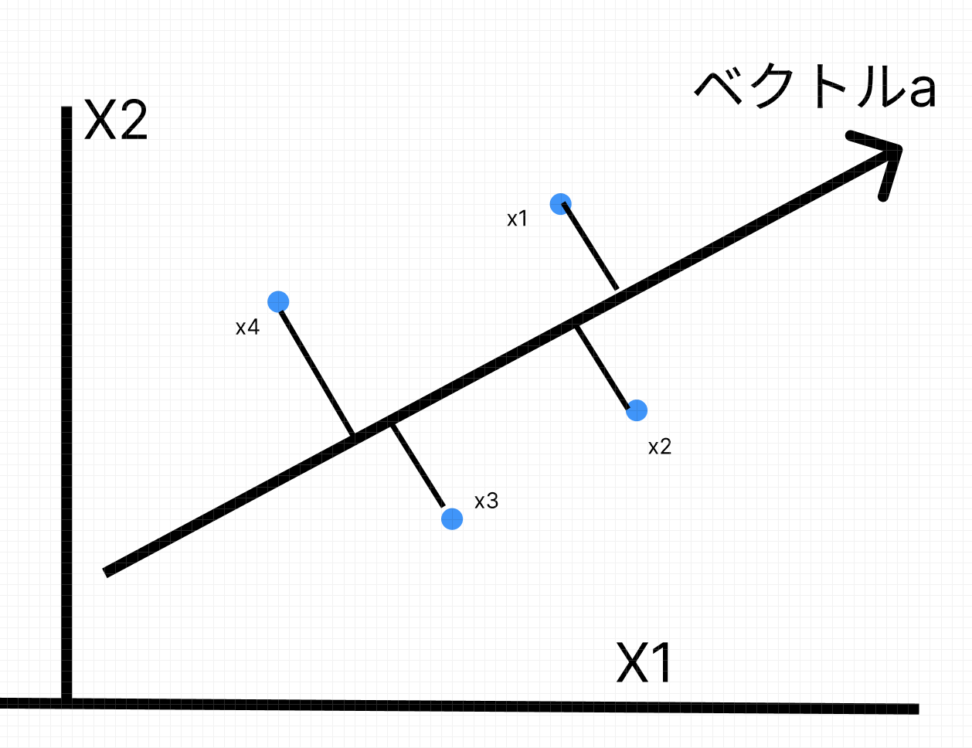
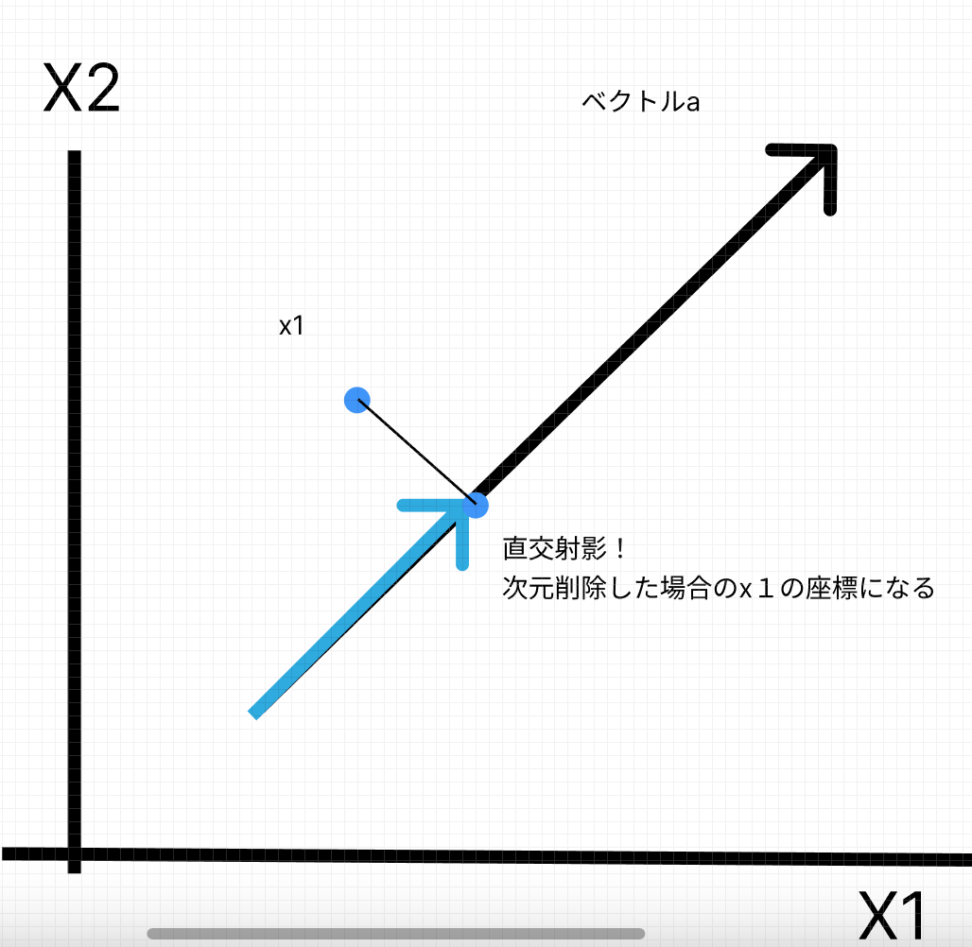
図示のために、観測データ4つと元の説明変数が2個の場合を想定しています。
ここでいうと\(a \cdot x_{1}\)はベクトル\(x_{1}\)のa方向の成分だとわかります。
以上のような幾何学的考察から、ベクトルaの適切な選び方としては、観測データのばらつきが最も大きい方向aを選ぶと言う方針になります。
つまり、以下のような制約付きの最適化問題を解くことになります。
$$\left\{\array{max \quad \sum_{i=1}^n(a \cdot x_{i}-a \cdot \overline{x})\\s.t \quad ||a||=1}\right.$$
固有値と固有値分解について
さて、上のような最適化で求められるaは次のような性質を持つと言われています
ただし\(f(a)= \sum_{i=1}^n(a \cdot x_{i}-a \cdot \overline{x})\)とします。
f(a)は行列\(X^TX\)の固有値であり、aはこの固有値に対する固有ベクトルである。
ただし行列Xについては、各成分を観測データの平均を使い中心化したものです。
$$\pmatrix{ x_{11}- \overline{x}_{1}&…&x_{1k}- \overline{x}_{k} \\ x_{n1}- \overline{x}_{1}&…&x_{nk}- \overline{x}_{k} }$$
さて、ここまで固有値と固有ベクトルと言う言葉が出てきました。
固有値とは、正方行列に対して定義される特別な値で、行列を掛け算すると自分自身のスカラー倍になるベクトルが存在する場合にそれを求めることができます。
このようなベクトルを固有ベクトルといいます。
固有ベクトルが存在する場合、そのベクトルに対応する固有値を持ちます(固有対)。
そして、固有値分解とは正方行列X^TXを対角化して、固有値と固有ベクトルに分解する処理のことです。
ここでは計算を省略しますが、今回の例においては以下のような関係が成り立ちます。
$$X^TXa = f(a)a $$
今回の例だと上のように表すことができます。
\(X^TX\)はn次元の正方行列であり、\(f(a)\)をAの固有値と言い、aは\(f(a)\)に属する固有ベクトルです。
正方行列は基本的には共分散行列を使います。
共分散行列は、各次元間の相関係数を要素とする正方行列であり、行列の対角成分には各次元の分散が含まれます。
また、共分散行列は、分散共分散行列に変換することで、標準偏差や相関係数による分析も可能です。
$$\pmatrix{ V(X_1)&COV(X_1,X_2)&…&COV(X_1,X_n) \\ COV(X_2,X_1)&V(X_2)&…&COV(X_n,X_1) \\ COV(X_n,X_1)&COV(X_n,X_2)&…&V(X_n)}$$
主成分分析においては、共分散行列が使用されることが多いですが、場合によっては、相関行列や正規化されたデータに対して主成分分析を行うこともあります。
図解：固有ベクトルについて
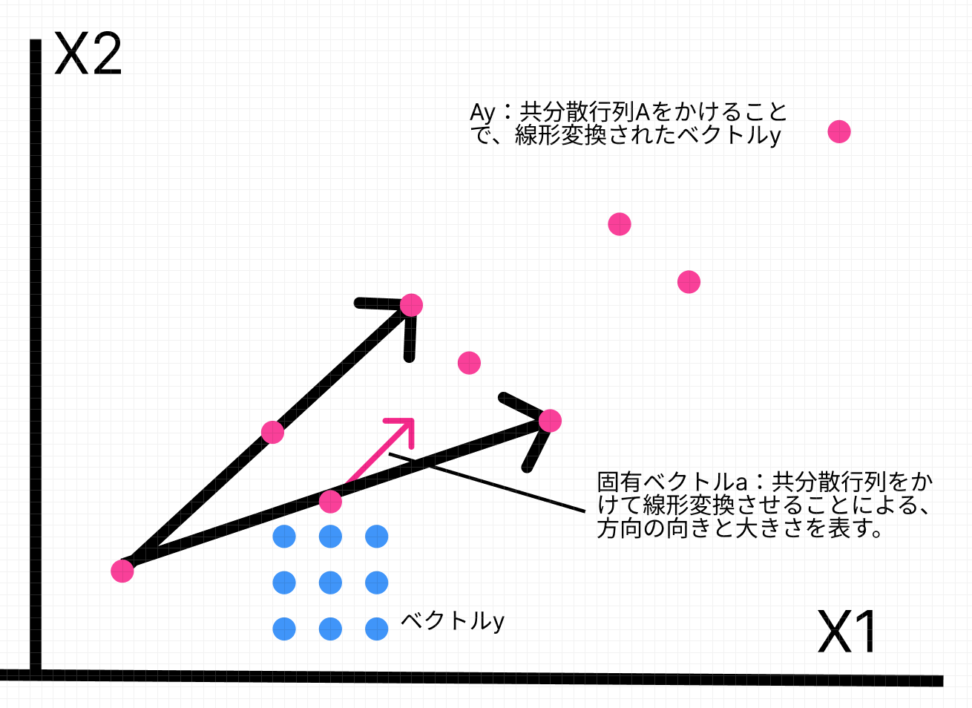
「ベクトルに正方行列をかける」ことがよくわからない方は上の図をご覧ください。
ベクトルyに対し、正方行列Aをかけることでベクトルyの転回や折り返しがされます。
固有ベクトルとは、ある正方行列Aをかけた時の「効果」です。
それは、変換される方向と大きさに分解できると言うことです。
線形変換の具体的な内容とは、標準基底による座標で表される点yを、行列Aの各点を新たな基点とした時の座標点Ayに変えているということです。
主成分分析では、このように正方行列を固有ベクトルと固有値に分解することによって、元のデータを低次元で表現することができます。
具体的には、正方行列を固有ベクトルと固有値の行列で表現する固有値分解を行い、固有値が大きい順に固有ベクトルを選び出して、元のデータを固有ベクトルに射影することで、データの特徴を抽出することができます。
固有値の大きさは、対応する固有ベクトルが表す主成分の重要性を示しています。
具体的には、最初の主成分が最も多くの分散を説明し、以降の主成分が少しずつ少なくなるような傾向があります。
つまり、最大の固有値を第一主成分として採用し、次は第二主成分…と採用していくわけです。
固有値の平方根と主成分の積を分散で割ったものが主成分負荷量になります。
主成分負荷量\(=frac{u_{i,j}\sqrt{λ}_{i}}{\sqrt{S}}\)
結論：主成分分析は線形変換??
ここまでで理解できることは、任意のベクトルを共分散行列の方向に線形変換するということです。
「共分散行列の方向」とは、固有ベクトル(データの分散方向)のことです。
なので、冒頭で示した通り主成分分析とは「共分散行列の固有ベクトルを求めること」とまとめることができます。
寄与率と累積寄与率
さて、求めた主成分が元々のデータの情報のうちどれくらいを説明できているかを評価する指標の一つとして「寄与率」と言うものがあります。
$$\frac{\frac{1}{n-1} \sum_{i=1}^n(a_{p} \cdot x_{i}-a_{p} \cdot \overline{x})}{\frac{1}{n-1} \sum_{i=1}^n ||x_{i}-\overline{x}||^2}$$
みて貰えばわかるとおり、元のデータのばらつきで主成分のばらつきを割ると計算できます。
実は分母は全主成分の固有値の和で表され、分子は該当主成分の固有値で表すことができます。
計算は省略します。
下は第一主成分の寄与率の例です。
$$\frac{f(a_{1})}{\sum_{l=1}^k f(a_{l})}$$
そして第1主成分からp主成分までを特徴量として用いた際に説明できるデータのばらつきの割合は累積寄与率と呼ばれ、単純にこれまでの寄与率を足し合わせると算出できます。
一般的には、80%までの累積寄与率が出せればそれ以降の主成分は不要と判断されます。
エルボー図などで、主成分による説明力を累積させたグラフを見れば、大体何次元まで主成分が必要かわかりますね。
主成分回帰とは(principal component regression)
主成分回帰では、まず説明変数に対して主成分分析を行い、主成分（新しい変数）とその重みを得ます。
次に、主成分を説明変数として回帰分析を行います。これにより、説明変数間の共線性問題を減らし、予測モデルの安定性と精度を向上させることができます。
主成分回帰は、説明変数間に高い相関関係がある場合に使用されます。
このような場合、従来の回帰分析では推定値が不安定になったり、大きなバイアスが生じる可能性があります。
主成分回帰は、説明変数の次元を低下させることによってこれらの問題を回避し、モデルの精度と信頼性を向上させることができます。
説明変数に高い相関があるときを多重共線性と呼びます。
多重共線性については以下のコンテンツをご覧ください。
【論文解説】多重共線性は回帰分析にどのような影響を与えるのか
【python】Ridge(リッジ)回帰で多重共線性を解決する話
CODE|python
主成分回帰についてコード例を紹介いたします。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import GridSearchCV, KFold
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# データの読み込み
cancer = load_breast_cancer()
X = cancer.data
y = cancer.target
seed = 42
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=seed)
# パイプラインの作成
pipe = Pipeline([
('scaler', StandardScaler()),
('pca', PCA()),
('reg', LinearRegression())
])
# ハイパーパラメータのグリッドサーチ
param_grid = {
'pca__n_components': [3, 5, 8],
}
kf = KFold(n_splits=5, shuffle=True, random_state=42)
grid = GridSearchCV(pipe, param_grid, cv=kf, scoring='neg_mean_squared_error')
grid.fit(X_train, y_train)
# 最適なモデルの取得
best_model = grid.best_estimator_
principal_components = pca.components_
# 交差検証によるモデル評価
scores = -1 * grid.cv_results_['mean_test_score']
print("Cross-Validation Scores:", scores)
# 主成分の寄与率の計算
pca = best_model.named_steps['pca']
explained_variance_ratio = pca.explained_variance_ratio_
# 累積寄与率の計算
cumulative_explained_variance_ratio = np.cumsum(explained_variance_ratio)
# 累積寄与率のグラフ化
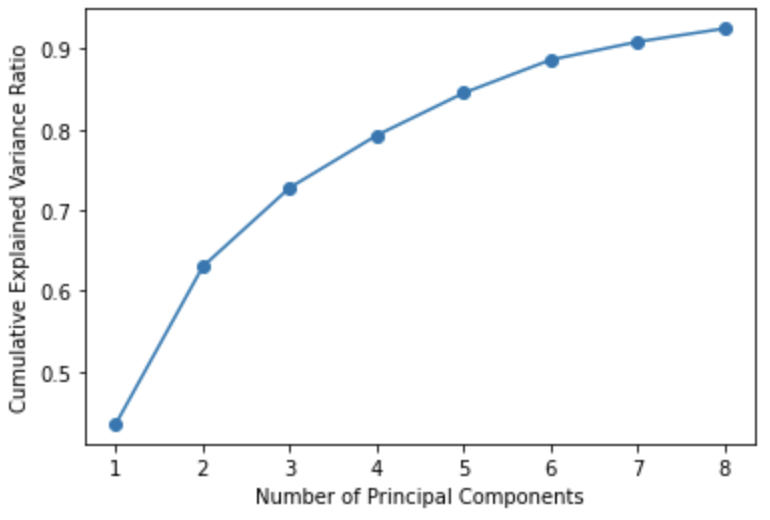
plt.plot(np.arange(1, len(cumulative_explained_variance_ratio)+1), cumulative_explained_variance_ratio, marker='o')
plt.xlabel('Number of Principal Components')
plt.ylabel('Cumulative Explained Variance Ratio')
plt.show()
Cross-Validation Scores: [0.07859532 0.07268389 0.07144949]
今回はpipelineを使って、正規化と主成分分析、線形回帰をおこなっております。
また、グリッドサーチにより主成分数の検討をおこなっていますが主成分数が多いほど精度は上がるのでbest_parametorとしては数が大きい方になります。
ただ、累積寄与率を見る限り主成分数は4か5くらいで良さそうですね。
また最後に主成分の係数を見てみましょう。
# 各主成分を格納した行列の表示
print(principal_components)[[ 0.21601485 0.1016996 0.22518147 0.21853483 0.14898157 0.24083587 0.25949969 0.26332425 0.14621735 0.06574066 0.20391855 0.0234544 0.20902392 0.19950297 0.02157185 0.16576253 0.14905441 0.18242981 0.04766427 0.09875333 0.22639195 0.10512288 0.2361263 0.22421579 0.13234785 0.21129704 0.22955601 0.25291716 0.1272409 0.13234079] [-0.24004016 -0.05126301 -0.22216079 -0.23648928 0.16931634 0.1501344 0.06403735 -0.03963956 0.18327955 0.3614473 -0.10885925 0.09695105 -0.09160367 -0.15364598 0.19446562 0.23790703 0.20784177 0.1430481 0.17450928 0.28110189 -0.22454754 -0.03899357 -0.20358556 -0.22266931 0.15618182 0.14403463 0.10278108 -0.00567144 0.13010012 0.27735365] .....
主成分分析の応用例
主成分分析は、さまざまな分野で広く利用されています。
例えば、金融分析においては、株式市場の複数の指標を主成分分析によってまとめ、市場全体の動きを把握することができます。
また、マーケティング分析においては、顧客の属性や行動などを多次元データとして扱い、顧客のニーズや嗜好を分析することができます。
さらに、主成分分析は、画像処理や音声認識などの分野でも応用されています。
画像処理では、画像の多次元データを主成分分析によって圧縮し、画像の特徴を抽出することができます。
音声認識では、音声波形を主成分分析によって特徴量に変換し、音声の識別精度を向上させることができます。
コラム|オートエンコーダと主成分分析
次元削除といえば、オートエンコーダも覚えておくと良いでしょう。
オートエンコーダは、以下のような2つの機構によって成り立っています。
エンコーダ：入力を読み出し、次元を圧縮する
デコーダ：圧縮された表現から元の入力を再構成する
結局は元の入力を表現するという点で、一体何の意味があるのかわからないと思います。
これは、計算資源の節約につながります。
主に自己符号化器(auto encoder)は、ニューラルネットワークモデルの中で扱われ、エンコーダによって元の特徴を残したまま、小さいサイズで情報を扱うことができます。
誤差逆伝播法によって学習されるので、一度学習して仕舞えばデコーダーを外してしまって次元削減のみ行うといった使い方も可能です。
G検定にも出題されており、こちらでも軽く触れているのでご一読ください。
