【python】行列式や逆行列は機械学習でどう使われるのか|線形代数の活用方法
大学数学で習う線形代数は、統計学や機械学習ではどのように活用されているのでしょうか？
なんとなく説明変数をたくさん書かなくても行ベクトル一つ書いておけば良いから楽、程度に考えているかもしれませんが、実はもっと役に立っております。
今回は、逆行列と行列式を中心にデータサイエンス領域での活用のされ方を概観します。
線形代数についてのコンテンツは、以下をご覧ください。
【線形代数】固有値や固有ベクトルは機械学習にどう使われているのか|主成分分析
【数理統計学】ヤコビアンをわかりやすく解説|MCMCでの使用例
逆行列(inverse matrix)と行列式(determinant)
逆行列は、正方行列Aに対して、以下の数式を満たす行列です。
$$ A×A^{-1} = A^{-1} × A = E $$
ここで、\(A^{-1}\)は逆行列、\(E\)は単位行列を表します。
元の行列と掛けると単位行列になるような行列のことですね。行列を分数の形で表すことはできませんが、意味的には逆数のようなものです。
ちなみに、上のような式が成り立つAを正則と呼びます。
正方行列であることが条件ですが、正方行列であれば必ず正則になるとは限りません。
pythonのコードを紹介します
import numpy as np
A = np.random.randint(-10, 10, size=(4,2,2))
inv_A = np.linalg.inv(A)
print(A)
print(inv_A)-10から10までの乱数を使って、2×2の正方行列を4つ作りました。
その後それらの逆行列を求めるメソッドの引数に入れたらおしまいです。
[[[ -7 -8] [ 3 -1]] [[ 6 -4] [ 3 7]] [[ -5 1] [ -4 -1]] [[ 7 -10] [ -7 -8]]] [[[-0.03225806 0.25806452] [-0.09677419 -0.22580645]] [[ 0.12962963 0.07407407] [-0.05555556 0.11111111]] [[-0.11111111 -0.11111111] [ 0.44444444 -0.55555556]] [[ 0.06349206 -0.07936508] [-0.05555556 -0.05555556]]]
そして逆行列は以下のように表されます
$$A^{-1}=A × \frac{1}{|A|} \tilde{A}$$
\(\tilde{A}\)に関しては、対角成分がAの行列式で他の成分が0の行列です。
$$\tilde{A} = \begin{pmatrix} |A| \\ & |A| & & \text{\huge{0}} \\ & & \ddots \\ & \text{\huge{0}} & & \ddots \\ & & & & |A| \end{pmatrix}$$
行列式は、正方行列Aに対して、以下の数式で定義されます。
$$det(A) = |A|$$
行列式は、行列が可逆であるかどうかを判定する際に利用されます。
具体的には、行列式が0でない場合、逆行列が存在し、行列が可逆であると言えます。
これは、機械学習や統計学の分野で、特に多変量正規分布や主成分分析など、多次元データの解析に使われます。
行列式は、numpyを使えば簡単に求めることができます。
import numpy as np
A = np.array([[1, 10, 3], [4, 4, 5], [2, 8, 12]])
det_A = np.linalg.det(A)
print(det_A)では逆行列や行列式がどう使われるのかを見ていきましょう。
線形回帰での使われ方
逆行列は、データサイエンスの分野で幅広く活用されています。
例えば、線形回帰分析では、最小二乗法を用いて、以下の数式を解きます。
$$β = (X^T× X)^{-1} × X^T×y$$
ここで、Xは説明変数の行列、yは目的変数のベクトル、βは回帰係数のベクトルを表します。
この数式を解くことで、目的変数と説明変数の関係をモデル化できます。
回帰については、こちらをどうぞ。
もう少し丁寧に目的関数から説明していきます。
線形回帰モデルの場合、最小二乗法の目的関数は次のように表されます。
$$J(w) = ||Xβ – y||^2$$
よく数式を見ていただければ、これがMSEだということに気づくはずです。
【MSEを最小化】ガウス・マルコフの定理と最良線形不偏推定量について
この目的関数を最小化するパラメータwを求めるために、目的関数を回帰ベクトルβについて微分し、0に等しいという条件(一階条件というやつです)を設けます。
$$∇J(w) = 0$$
この式を解くと、以下の正規方程式が得られます。
$$X^T X β = X^T y$$
逆行列を用いることで、この正規方程式の解析解を求めることができます。
$$β = (X^T X)^{-1} X^T y$$
リッジ回帰での使われ方
次に過学習を防ぐためにL2正則化項を加えたリッジ回帰について解説します。
【python】Ridge(リッジ)回帰で多重共線性を解決する話
【python】Lasso(ラッソ)回帰で疎なデータに対応しよう|機械学習
リッジ回帰の最適化問題は以下のように表されます。
$$minimize J(w) = ||Xw – y||^2 + λ||w||^2$$
ここで、wは重みベクトル、Xはデータ行列、yは目的変数ベクトル、λは正則化パラメータです。
リッジ回帰の解析解は以下のように逆行列を用いて求められます。
$$w = (X^T X + λI)^{-1} X^T y$$
この解析解を用いることで、リッジ回帰の学習が効率的に行われます。
あれ？勾配降下法使わないの？？
と思った方も多いと思います。
上のように解析的に求めると(求められるならば)、勾配降下法のような近似的な計算をしなくても最適な解が出ます。
実は、pythonライブラリのscikit-learnのLinearRegressionクラスは、解析解を求めています！
下のように、損失関数を最小化するパラメータを探索する方法が最急勾配降下法でした。
損失関数が \(L(w1, w2, …, wn\) で表される場合、勾配は各パラメータに対する損失関数の偏微分から構成されるベクトルです。
勾配が示す方向は、損失関数の値が最も急速に増加する方向なので、勾配が最も大きい方の逆に進んでいけば、損失関数はどんどん小さくなることになります。
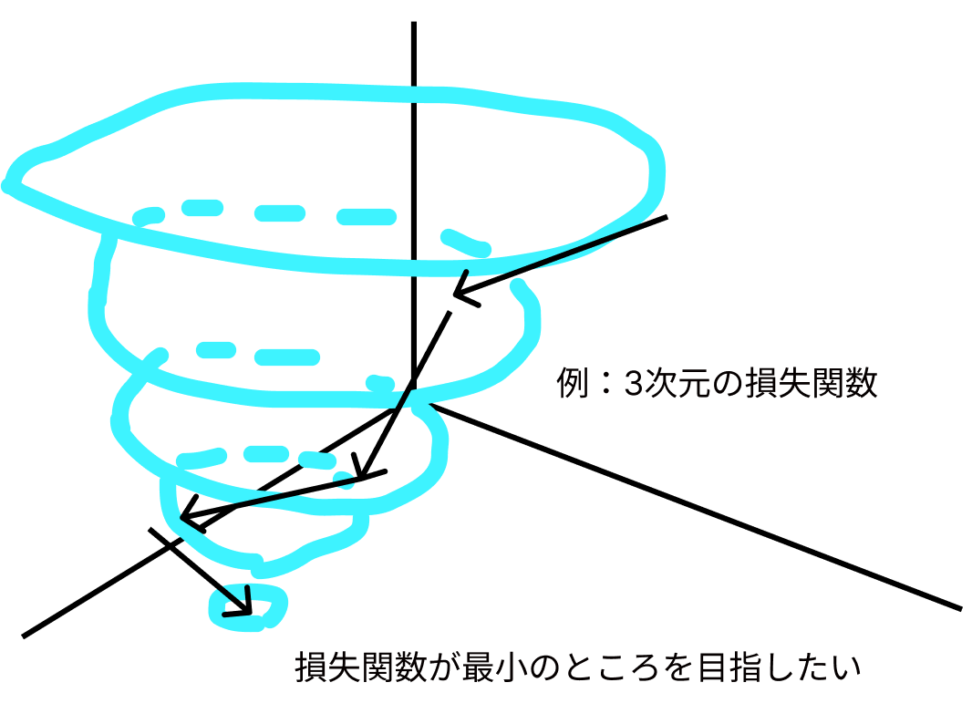
勾配降下法は、線形回帰以外のアルゴリズム（例：ニューラルネットワーク）や、リッジ回帰、LASSOなどの正則化付き線形回帰で利用されることが一般的です。
これらのアルゴリズムでは、勾配降下法や確率的勾配降下法（SGD）などの最適化手法を用いて、近似解を求めます。
回帰タスクにおいては、解析解を求めることができる場合がありますが、説明変数を格納した列ベクトルの状態によっては、解析解が求められない状況も存在します。
計算コストが大きすぎて解析的に解けない場合もありますが、主要なものは多重共線性です。
多重共線性が認められる場合
説明変数間に高い相関がある場合（多重共線性）、データ行列Xがほぼシンギュラー(特異行列となり、行列式が0になる)になることがあります。
この場合、逆行列が存在しても、数値的な不安定性が生じ、計算が収束せず、解析解が不正確になることがあります。
リッジ回帰などの正則化手法や、変数選択・次元削減手法（例：主成分分析）を用いて問題を緩和することができます。
また、最悪のケースとして行列式が0の場合、逆行列が存在しないため、解析解は求められません。
この場合、数値最適化アルゴリズム（例：勾配降下法）を用いて近似解を求めることが一般的です。
【論文解説】多重共線性は回帰分析にどのような影響を与えるのか
そもそも多重共線性があるとなぜ特異行列に近づくのか？
説明変数間に強い相関がある場合、データ行列Xの列ベクトルが線形従属（一方が他方の線形結合で表される）に近くなります。
これにより、行列\(X^T X\)はランクが不足し、特異行列に近づくことがあります。
定量的には\(rank(A)<n\)で多重共線性があると言われます。
$$\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ k a_{11} & k a_{12} \end{bmatrix}$$
特異行列は逆行列が存在しないため、連立方程式が一意的な解を持たない（つまり、線形代数でいう不能）ことを意味します。
例えば式が4個しかないのに、変数を5個以上求めなければならないということです。
これは中学生でも「解けない(解析的には)」と感じられるはずです。
$$\begin{cases} a_{11} x_1 + a_{12} x_2 + a_{13} x_3 + a_{14} x_4 + a_{15} x_5 = b_1 \\ a_{21} x_1 + a_{22} x_2 + a_{23} x_3 + a_{24} x_4 + a_{25} x_5 = b_2 \\ a_{31} x_1 + a_{32} x_2 + a_{33} x_3 + a_{34} x_4 + a_{35} x_5 = b_3 \\ a_{41} x_1 + a_{42} x_2 + a_{43} x_3 + a_{44} x_4 + a_{45} x_5 = b_4 \\ 0 = 0 \end{cases}$$
