【自然言語処理】検索クエリをベクトル空間に写像してクラスタリングしたい
こんにちは、青の統計学です。
筆者の業務で使うので、勉強がてらまとめていきます。
参考となるコードも紹介していますので、ぜひ最後までご覧ください。
タスクについて|検索クエリの分析について
以下のようなことに挑戦してみます。
事業会社のマーケティング部門で有料集客の最適化を行うとします。
google ads による出稿を行なっており、google側の広告最適化の邪魔をしないためにデータサイエンティスト側で動かせるレバーはわずかです。
レバー
・マッチタイプ:google側が 部分一致:それ以外=7:3 を推奨しており、最適化の邪魔をしないためにもここは介入余地なし
・広告文:広告文とキーワードの候補から、最適なオーディエンスに対して最適なクリエイティブを生成して、リスティング広告としてgoogleがぶつけているので介入余地なし
・LP:広告グループごとに設定している、遷移先のLPに対して、広告文と齟齬が生じて高CTRかつ低CVRが生じて費用が嵩んでいるのではないか。検索クエリにあったLP最適化はgoogle側では介入できないので、ここにデータサイエンティストの介在価値があるのではないか。
・入札戦略:ここは自動入札が推奨されているので、介入余地なし
タスク
google adsで自身のサイトのリスティング広告に引っかかった検索クエリ分析
仮説
「検索クエリによっては、リスティング広告のLP(ランディングページ)と検索者のインテントが合わないのでは?」
やること
同じ広告グループに引っかかった、複数の検索クエリをベクトル空間に埋め込んで、クラスタリングしてみる
CODE|tokenization
クエリをword2vecで埋め込みし、ベクトル空間に写像します。
その後に、コサイン類似度を使ったクラスタリングを行い、3つの主成分で可視化してみたいと思います。
import pandas as pd
# CSVファイルを読み込む
df = pd.read_csv('ads_query.csv')
# 検索クエリの列を取り出す
queries = df.iloc[:, 1]| queryId | query | cv |
| 1 | データサイエンス 勉強 | 0 |
| 2 | 統計学 大学 | 0 |
| 3 | データ分析 資格 | 3 |
| 4 | 機械学習 | 1 |
| 5 | 機械学習 勉強方法 | 1 |
このような形で、CV数(サイト内でのなんらかのイベント)と検索クエリがデータフレーム形式になっております。
今回は仮で作ったデータで遊んでみるだけなので、どこかにデータの参照先があるわけではございません。ご容赦ください。
import nltk
from nltk.tokenize import word_tokenize
nltk.download('punkt')
def tokenize_with_nltk(text):
return word_tokenize(text)
# 全てのクエリをトークン化
tokenized_queries = [tokenize_with_nltk(q) for q in queries]
tokenized_queries次に、検索クエリの列を抽出してトークンにします。
以下のように分割されました。
[['データサイエンス', '勉強'], ['統計学', '大学'], ['データ分析', '資格'], ['機械学習'], ['機械学習', '勉強方法'], ['統計検定準1級チートシート'], ['応用情報', 'チートシート'], ['尤度比検定', 'わかりやすく'], ['尤度比検定'], ['傾向スコアマッチング', 'python'], ['スピアマンの順位相関係数', 'python'], ['統計検定2級', 'チートシート'], ['最尤推定法', '例題'], ['leave', 'one', 'out', 'python'], ['多重共線性'], ['活性化関数', '選び方'], ['マルチンゲール', 'わかりやすく'], ['ポアソン過程', 'わかりやすく'], ['python', '階層型クラスタリング'], ['コサイン類似度', '計算', 'サイト'], ['不偏性', 'わかりやすく'], ['kaggle', '統計検定'], ['コサイン類似度', '相関係数'], ['gbdt', 'python'], ['回帰不連続デザイン', 'わかりやすく'], ['機械学習', '寄与度'], ['ランダムフォレスト', 'ブートストラップ'], ['cnn', '画像認識', 'python'], ['did分析', 'わかりやすく'], ['word2vec', 'クラスタリング']]
トークナイズとは、テキストをより扱いやすい形に変換するための前処理手法の一つです。
具体的には、テキストを小さな単位(通常は単語、部分文字列、またはシンボル)に分割します。この過程で、句読点や空白、特殊文字なども取り扱います。
CODE|embedding
from gensim.models import Word2Vec,KeyedVectors
model_dir = '../dictionary_NLP/entity_vector/entity_vector.model.bin'
model = KeyedVectors.load_word2vec_format(model_dir, binary=True)
model = Word2Vec.load("word2vec.model")
#クエリをベクトルに変換(各トークンのベクトルの平均を取るなど)
query_vectors = []
for tokens in tokenized_queries:
vectors = [model[token] for token in tokens if token in model.index_to_key]
if vectors: # 空でない場合のみ平均を計算
vec = sum(vectors) / len(vectors)
query_vectors.append(vec)
else: # 空の場合は、何らかのデフォルト値(例えばゼロベクトル)を用いる
query_vectors.append(np.zeros(model.vector_size))では、トークナイズした検索クエリを埋め込み(単語の分散表現とも呼びます)して、ベクトル空間に写像してみましょう。
word2vecでは、入力した単語を中心と捉え、前後の文字n文字の文字の正規確率を最大化するようなパラメータを探索します。
少しword2vecで使われている、skipgramアルゴリズムの説明をします。
$$J = \frac{1}{T} \sum_{t=1}^{T} \sum_{-m \leq j \leq m, j \neq 0} \log p(w_{t+j} | w_t)$$
\(T\)はコーパス内の総単語数
\(m\)はウィンドウサイズ(中心単語の前後にどれだけの単語を見るか)
\(w_t\)は時刻\(t\)における単語
ここの中心単語\(w_t\)が与えられた時の周辺単語\(w_{t+j}\)が現れるという条件付き確率は以下のようにソフトマックス関数で表されます。
$$p(w_O | w_I) = \frac{\exp(v_{w_O}^{\prime T} v_{w_I})}{\sum_{w=1}^{W} \exp(v_w^{\prime T} v_{w_I})}$$
\(w_L\) は入力単語(中心単語)、\(w_O\) は出力単語(周囲の単語)
\(v_w\)と\(v_w’\)はそれぞれ単語 \(w\)の入力側と出力側のベクトル
Wは語彙数
ソフトマックス関数については、以下のコンテンツでご覧いただけます。
以下のコンテンツでも紹介しましたが、gensimというword2vecのライブラリを使ってみます。
【自然言語処理】gensimを使った単語の分散表現|python
辞書として、東北大のwikipediaのエンティティベクトルを使用しています
「日本語 Wikipedia エンティティベクトル」は、日本語版 Wikipedia の本文全文から学習した、単語、および Wikipedia で記事となっているエンティティの分散表現ベクトルです。
Wikipedia の記事本文の抽出には WikiExtractor を、単語分割には MeCab を、単語ベクトルの学習には word2vec をそれぞれ用いています。
CODE|clustering
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.cluster import AffinityPropagation
# コサイン類似度の計算
similarity_matrix = cosine_similarity(query_vectors)
# Affinity Propagationによるクラスタリング
clustering = AffinityPropagation(affinity='precomputed', preference=-0.5).fit(similarity_matrix)
labels = clustering.labels_ベクトル間の内積を利用して、検索クエリの類似度を測るためにコサイン類似度を使っています。
詳しい仕組みは以下をご覧ください。
【python】コサイン類似度は高校数学の知識で理解できます!|自然言語処理
ここのクラスタリングの手法は、分析目的によって変わると思います。
今回のコサイン類似度の他にも、Kmeansを使ったり、DBSCANを使ったりなどできます。
この二つは、コサイン類似度とは違い、クラスター数を事前に設定することはできますが、前もって「この広告グループに引っ掛かる検索クエリはDo系のクエリかBuy系のクエリだろう、なぜなら広告文が~だからだ。」のような、仮説が必要だと思います。
余談|言語モデルのdata pruningについて
大規模言語モデルのデータ刈り込み(Data Pruning)の文脈で、データを自己教師あり学習済みの埋め込み(Embeding)モデルに通して、潜在空間上でK-means法によってクラスタリングを行い、クラスタの中心点からの(コサイン)距離でサンプルの難易度を決定する
→学習データが少ない場合は、難易度が低いサンプルを多く残し
→学習データが多い場合は、難易度が高いサンプルを多く残す
のような取り組みがあり、本件とちょっと似ているなと思いました。
これは、クラスターの決定境界に近いほど、サンプルの難易度が高いという考えに基づいています。
以下の論文に詳細はあります。
Beyond neural scaling laws: beating power law scaling via data pruning
階層型クラスタリングと、非階層型クラスタリングについては以下のコンテンツをご覧ください。
【非階層型】K-means法でクラスタリングをしてみましょう。
【python】階層型クラスタリングとデンドログラムの実装について
CODE|visualization
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
# クラスタごとに色を分けて3Dプロット
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
unique_labels_cosine = set(labels) # 実際のクラスタラベルを使用
for label in unique_labels_cosine:
points = [reduced_vectors_3d[i] for i in range(len(labels)) if labels[i] == label]
points = np.array(points)
ax.scatter(points[:, 0], points[:, 1], points[:, 2], label=f'Cluster {label}')
ax.set_title('Clustering of Queries in 3D using Cosine Similarity')
ax.set_xlabel('Principal Component 1')
ax.set_ylabel('Principal Component 2')
ax.set_zlabel('Principal Component 3')
ax.legend()
plt.show()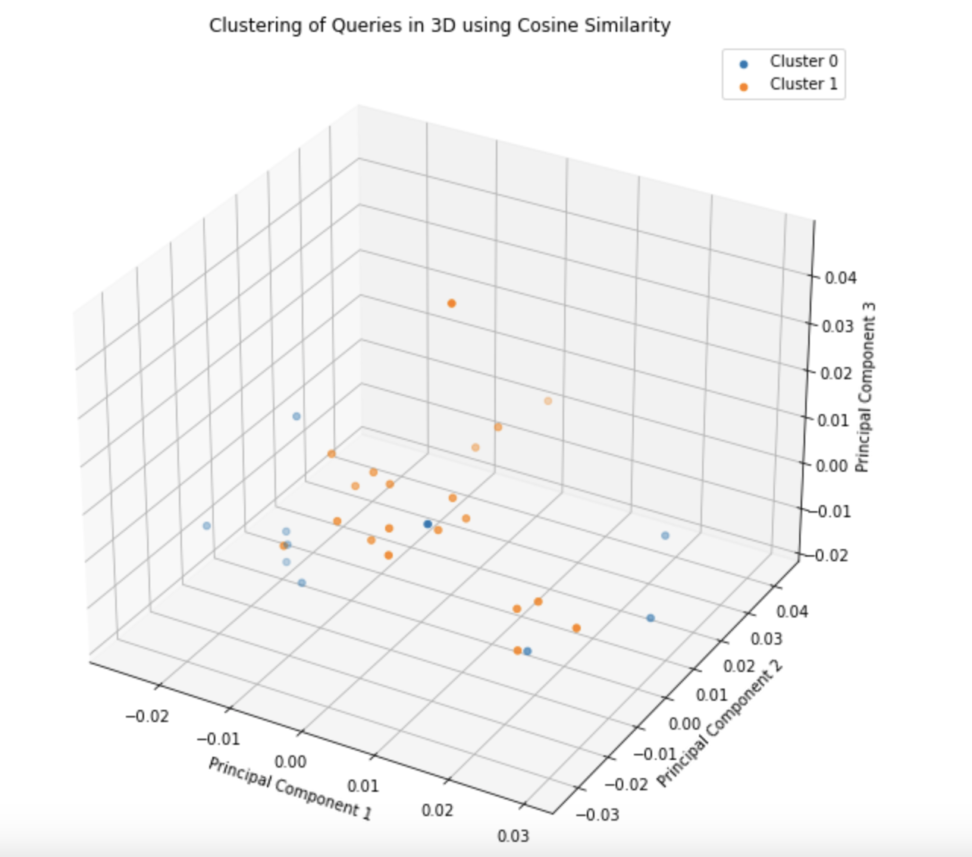
クラスタリングした内容を可視化するために3つの主成分で見てみます。
このように二つのクラスターに分かれている様子が見受けられます。
主成分分析については、以下のコンテンツをご覧ください。
【線形代数】固有値や固有ベクトルは機械学習にどう使われているのか|主成分分析
【共線性解決!?】pythonで主成分分析(PCA)をやってみた
【python】主成分分析(+回帰)の仕組みとコード例|教師なし学習
人間の目でクラスターに分けたプロットが見える限界が3次元なので、3つの主成分で表しました。
これは、query_vectorsを説明し切れれているのでしょうか?
エルボー図を見てみます。
# 全ての主成分を計算
pca_all = PCA(n_components=None)
pca_all.fit(query_vectors)
explained_variances = pca_all.explained_variance_ratio_
# エルボー図の作成
plt.figure(figsize=(10, 6))
plt.plot(range(1, len(explained_variances) + 1), explained_variances, marker='o')
plt.xlabel('Number of Components')
plt.ylabel('Explained Variance')
plt.title('Elbow Plot')
plt.show()
# 寄与度の合計を計算(最初の3つの主成分で)
print("Total explained variance by first 3 components:", sum(explained_variances[:3]))
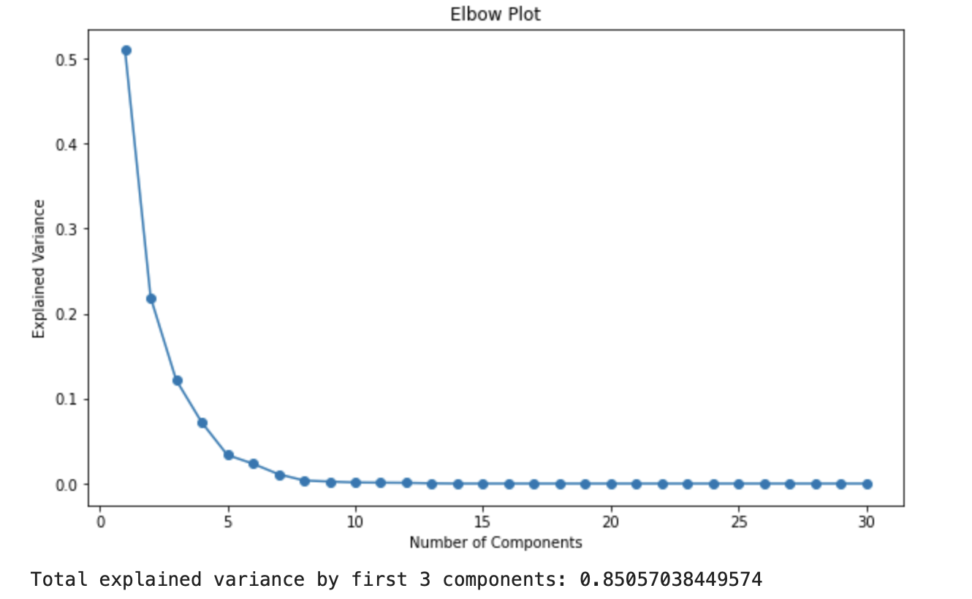
累積寄与度を見ると、3つの主成分で8割の分散を説明できているので、次元削減としては十分かなといったところです。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


