階層型クラスタリングとデンドログラムを解説|k-means法との比較
こんにちは、青の統計学です。
今回は、階層型のクラスタリングについて解説しようと思います。
なぜ「階層」で考えるのか?
非階層的なクラスタリング手法、例えばk-means法では、事前にクラスタの数($k$)を決める必要があります。しかし、データに内在する真の構造がいくつあるかは、分析を始める前には当然わからないですよね。
階層型クラスタリングの大きな特徴は、この「クラスタの数」を固定せず、データ点一つひとつから始まり、最終的にすべてを一つの大きなグループにまとめるまでの全過程を数学的に記述できるという点にあります。

今回は、非階層型のクラスタリングのkmeansと比較していきます。復習をしたい方は以下の記事をご覧ください。
データ点の関係性を定義する|ユークリッド距離
階層型クラスタリングの出発点は、データ点とデータ点の間の近さを測ることです。この「近さ」を測る尺度が距離(非類似度)であり、その選択がクラスタリングの結果を決定づけると言っても過言ではありません。
最も一般的に用いられるのはユークリッド距離です。
私たちが日常で使う「直線距離」を多次元空間に拡張したものです。2つのデータ点 $p = (p_1, p_2, \dots, p_n)$ と $q = (q_1, q_2, \dots, q_n)$ の間のユークリッド距離 $d(p, q)$ は、以下の数式で定義されます。
$$d(p, q) = \sqrt{\sum_{i=1}^{n} (q_i – p_i)^2}$$
中学生でも習う、「直線の距離が一番短い」的な問題でやる計算と同じですね。ユークリッド距離は、各特徴量の値の差を二乗して足し合わせるため、大きな差が結果に強く反映されます。
一方、特徴量の軸に沿った移動距離の合計で測るマンハッタン距離(L1ノルム)など、他にも様々な距離尺度があり、分析の目的に応じて使い分けられます。例えば、外れ値の影響を抑えたい場合はマンハッタン距離が好まれることがあります。

距離尺度の選択は、「データ点間のどのような違いを重要視するか」という、分析者の意図を数学的に表現する行為というわけですね。
今回は、この距離計算の方法を網羅的に解説するわけではないので、興味がある方はご自身で調べてみてください。
距離尺度の概観
ユークリッド距離
$$\sum_{i=1}^n(x_{i}-y_{i})^2$$
マンハッタン距離
$$\sum_{i=1}^n|x_{i}-y_{i}|$$
マハラノビス距離
$$\sqrt{(x_{i}-y_{i})^T\sum^{-1}(x_{i}-y_{i})}$$
*マハラノビス距離は相関関係を考慮した距離尺度になっており、真ん中の項に分散共分散行列が用いられています。
連結方法という考え方
階層型クラスタリングには、大きく分けて「凝集型(Agglomerative)」と「分割型(Divisive)」の2種類がありますが、実務で最も使われるのは、個々のデータ点から始めて徐々にクラスタを併合していく凝集型です。
凝集型クラスタリングでは、データ点間の距離だけでなく、クラスタとクラスタの間の距離をどのように定義するかが次のステップになります。これを連結方法(Linkage Method)と呼びます。
| 連結方法 | クラスタ間の距離の定義 | 特徴と結果の傾向 |
| 最近隣法 | 2つのクラスタ間で最も近いデータ点間の距離 | 細長いクラスタ(鎖状のクラスタ)を形成しやすい(Chaining Effect) |
| 最遠隣法 | 2つのクラスタ間で最も遠いデータ点間の距離 | 比較的コンパクトで球状のクラスタを形成しやすい |
| 群平均法 | 2つのクラスタに属するすべてのデータ点ペアの平均距離 | 最近隣法と最遠隣法の中間的な性質を持つ |
| ウォード法 | クラスタを併合した際のクラスタ内平方和の増加量 | クラスタ内の分散を最小化するように併合。最もバランスの取れたクラスタを形成しやすい |
特にウォード法は、広く利用されています。
ウォード法は、クラスタを併合したときに、そのクラスタ内のデータのばらつき(分散)が最も小さくなるように、つまり「最も均質なグループ」を作るように併合を進めます。
詳しくはこちら↓
階層型クラスタリング徹底比較|ウォード法・最短距離法などの使い分け
これは、統計学でいう分散分析(ANOVA)の考え方に近く、クラスタ内の分散を小さく保ち、クラスタ間の分散を大きく保つことを目的としています。
ウォード法におけるクラスタ $A$ と $B$ の併合は、クラスタ内平方和(Within-Cluster Sum of Squares, WCSS)の増加 $\Delta(A, B)$ を最小化するように行われます。
$$\Delta(A, B) = \frac{n_A n_B}{n_A + n_B} \| \bar{x}_A – \bar{x}_B \|^2$$
- $n_A, n_B$ はクラスタ $A, B$ のデータ点の数
- $\bar{x}_A, \bar{x}_B$ はそれぞれのクラスタの重心(平均ベクトル)
デンドログラム:階層構造を可視化する「系統樹」
階層型クラスタリングの結果は、デンドログラム(Dendrogram)という樹形図で表現されます。デンドログラムは、データ点やクラスタがどのように併合されていったかの過程を視覚的に示してくれる系統樹です。ちなみに、統計検定準一級の試験範囲にもなっています。
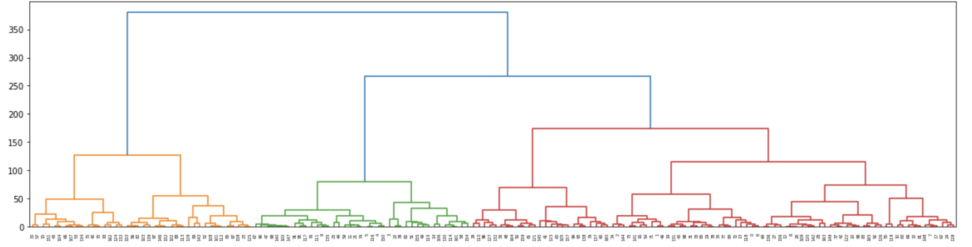
デンドログラムの縦軸は、クラスタが併合されたときの距離(非類似度)、つまり「高さ」を表します。この高さが低い位置で結合しているデータ点やクラスタほど、互いに「近い」関係にあることを意味します。
結果として出力される樹形図から、分類の過程でできるクラスターがどのように結合されていくのか確認できるというのは、結果を解釈するという観点でも嬉しいですね、

階層構造を扱うので、決定木っぽいですね!とはいえ決定木が「予測」のために階層構造を利用するのに対し、階層型クラスタリングは「理解や解釈」のために階層構造を利用すると考えると役割の整理がつきそうです。
冒頭でも言及した通りで、デンドログラムの嬉しいポイントは、クラスタ数を分析者が自由に決定できる点にあります。デンドログラムを水平な線で切ることで、その線が交差する縦線の数が、その距離レベルにおけるクラスタの数となります。
メリットばかりを述べてしまっていますが、K-means法とは異なりクラスター数を事前に決めなくて良いが、距離尺度(ユークリッド距離)と併合方法(ウォード法,中心法,群平均)をハイパーパラメータとして設定する必要はあります。
他の概念との繋がり
非階層クラスタリング(k-means法)との違い
k-means法は、事前に決めた $k$ 個のクラスタにデータを「割り当てる」手法です。これは、データ構造をパーティション(分割)として捉えます。
一方、階層型クラスタリングは、データ構造をネストされた階層として捉えます。この違いは、分析の目的に応じたトレードオフを生みます。
| 比較項目 | 階層型クラスタリング | k-means法 |
| クラスタ数 | 後からデンドログラムを見て決定(柔軟) | 事前に $k$ を決定する必要がある(硬直) |
| クラスタ形状 | 連結方法により多様な形状に対応可能 | 基本的に球状のクラスタを想定 |
| 計算量 | データ点数 $N$ に対して $O(N^3)$ または $O(N^2)$ | $O(N \cdot k \cdot I)$ ($I$は反復回数)で、大規模データに強い |
| 結果の解釈 | 階層構造全体を俯瞰でき、詳細な関係性が分かる | 最終的なクラスタのみが得られる |
階層型クラスタリングは、データ点間の詳細な関係性を理解したい小〜中規模のデータや、クラスタ数が不明な探索的分析に適しています。k-means法は、計算効率が高く、大規模データの高速なグループ分けに適しています。
次元削減との関係性:主成分分析(PCA)
主成分分析(PCA)は、データの情報を保ちつつ次元を削減する手法です。PCAは、データ全体のばらつきを最もよく説明する軸(これが主成分)を見つけ出します。
クラスタリングとPCAは、しばしば組み合わせて使われます。
- PCAで次元削減
- 高次元のデータを2次元や3次元に落とし込み、ノイズを減らす。
- クラスタリング
- 削減された低次元空間で階層型クラスタリングを実行する。
事例|遺伝子発現解析
階層型クラスタリングは、バイオインフォマティクスの分野、特に遺伝子発現解析でよく使われます。
細胞の種類や病気の有無によって、遺伝子の「発現量」がどのように変化するかを調べるとき、デンドログラムで視覚的に表現します。
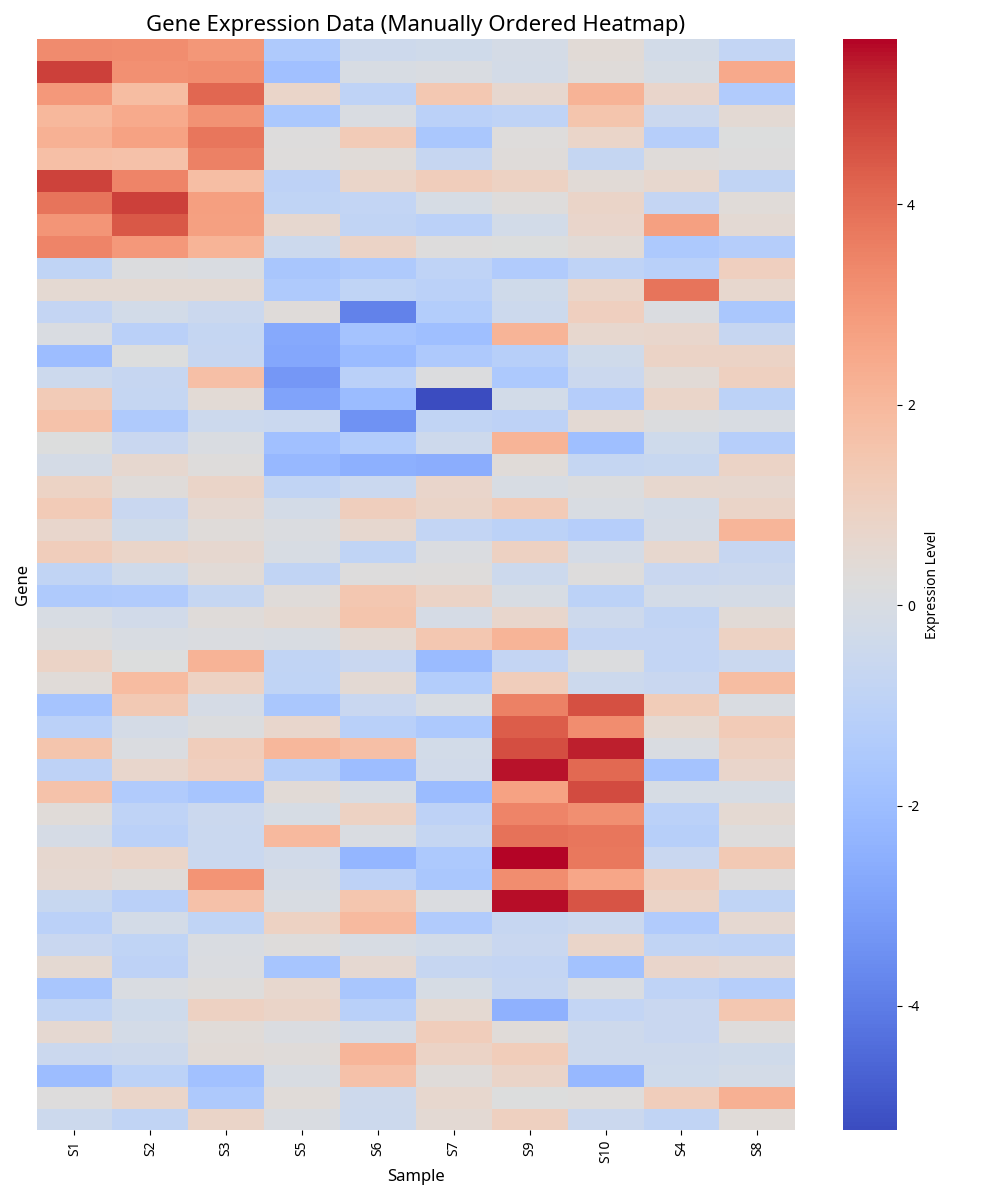
- 遺伝子のクラスタリング
- 似たような発現パターンを示す遺伝子同士をグループ化します。同じクラスタに入った遺伝子は、生物学的に同じ機能を持っている可能性が高いと推測
- サンプルのクラスタリング
- 異なる細胞サンプルや患者サンプルをクラスタリングします。これにより、病気のサブタイプや、治療法に対する反応が似ている患者群を客観的に特定する。
事例|テストの分布からクラスタリング
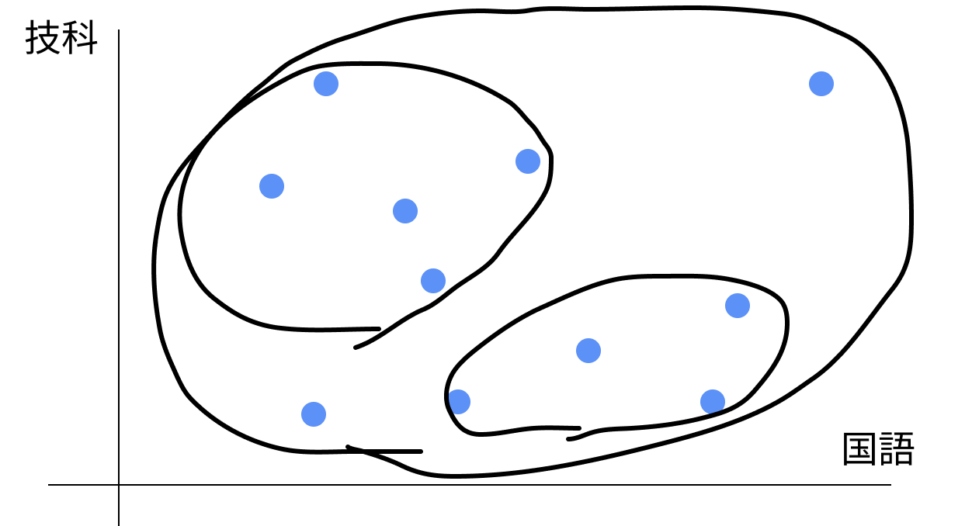
今回は、国語と技術のテストの点数から生徒をクラスタリングしてみようと思います。
#各ライブラリの読み込み
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import sklearn
#データの読み込み
seiseki = pd.read_csv('seiseki.csv')
seiseki
SeisekiList = []
for i in range(len(seiseki)):
SeisekiList.append([seiseki["kokugo"][i], seiseki["gika"][i]])
SeisekiListライブラリを読み込みます。今回のデータは、以下のようになっています。列としてはgika(技科)とkokugoを使います。
| kokugo | shakai | sugaku | rika | ongaku | bijutu | taiiku | gika | eigo | |
| 0 | 30 | 43 | 51 | 63 | 60 | 66 | 37 | 44 | 20 |
| 1 | 39 | 21 | 49 | 56 | 70 | 72 | 56 | 63 | 16 |
| 2 | 29 | 30 | 23 | 57 | 69 | 76 | 33 | 54 | 6 |
| 3 | 95 | 87 | 77 | 100 | 77 | 82 | 78 | 96 | 87 |
| 4 | 70 | 71 | 78 | 67 | 72 | 82 | 46 | 63 | 44 |
| … | … | … | … | … | … | … | … | … | … |
データフレームから目的の要素を抽出して、多重配列に入れます。
多重配列は、多次元配列とも呼ばれるもので、リストの中にリストが入っている構造です。
import numpy as np
X = np.array([[30, 44],[39, 63],[29, 54],[95, 96],[70, 63],[67, 66],[29, 43],[56, 67],[45, 46],[68, 72],[50, 65],[70, 67], [46, 45],[23, 48],[77, 88],[15, 17],[37, 55],[55, 68],[0, 6],[35, 39],[60, 57],[70, 70],[82, 99],[44, 22], [54, 61],[80, 68],[46, 46], [48, 52], [51, 41], [37, 35], [31, 7], [35, 33], [50, 60], [33, 33], [27, 58], [36, 49], [77, 49], [61, 52], [84, 100], [78, 44], [7, 18], [57, 38], [60, 52], [17, 9], [82, 61], [37, 40], [40, 62], [72, 74], [74, 50], [87, 73], [66, 51], [90, 68], [43, 31], [24, 11], [41, 55], [42, 90], [33, 20], [29, 4], [83, 84], [73, 69], [66, 33], [71, 55], [62, 61], [47, 65], [53, 51], [61, 34], [21, 10], [74, 77], [72, 74], [50, 57], [5, 18], [32, 61], [23, 37], [34, 55], [70, 69], [9, 17], [61, 74], [34, 45], [38, 35], [72, 37], [32, 21], [52, 59], [96, 75], [58, 45], [35, 47], [40, 36], [48, 25], [46, 26], [32, 27], [50, 13], [76, 73], [64, 80], [62, 44], [76, 32], [81, 35], [69, 78], [89, 51], [27, 23], [39, 39], [62, 55], [73, 72], [49, 32], [35, 27], [36, 20], [16, 11], [60, 30], [74, 92], [22, 11], [47, 33], [43, 49], [84, 44], [65, 70], [49, 33], [31, 29], [83, 78], [87, 76], [68, 66], [68, 77], [28, 47], [42, 85], [42, 45], [70, 52], [58, 55], [57, 31], [8, 5], [44, 21], [65, 43], [81, 51], [57, 59], [64, 7], [86, 79], [34, 38], [84, 50], [4, 4], [23, 13], [66, 72], [53, 50], [70, 27], [78, 32], [39, 23], [74, 74], [33, 53], [43, 46], [54, 18], [26, 54], [58, 24], [29, 23], [73, 73], [59, 67], [58, 52], [70, 61], [19, 19], [29, 24], [32, 19], [77, 82], [91, 74], [50, 49], [63, 31], [42, 20], [68, 49], [70, 32], [82, 78], [0, 2], [45, 40], [73, 48], [60, 45]])インデックスのリストを指定して値を取得するのは、Python の組み込みのリストでは対応していないで、numpy の ndarray を使います。
#サンプルデータの可視化
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(1,1,1,title="test")
plt.scatter(X[:,0],X[:,1])
for i, element in enumerate(X):
plt.text(element[0]+0.02,element[1]+0.02,i)
plt.show() 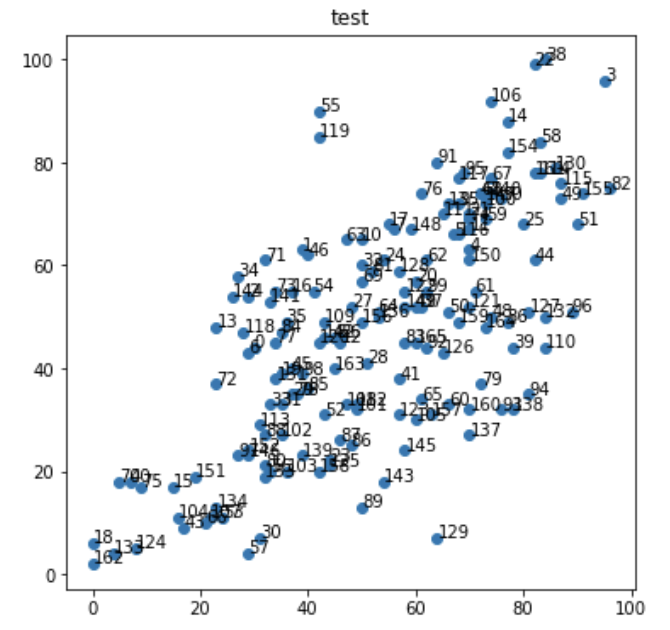
#階層型クラスタリング
#ウォード法
from scipy.cluster.hierarchy import linkage
Z = linkage(X,method="ward",metric="euclidean")
pd.DataFrame(Z)| 0 | 1 | 2 | 3 | |
| 0 | 47.0 | 68.0 | 0.000000 | 2.0 |
| 1 | 5.0 | 116.0 | 1.000000 | 2.0 |
| 2 | 8.0 | 26.0 | 1.000000 | 2.0 |
| 3 | 21.0 | 74.0 | 1.000000 | 2.0 |
| 4 | 23.0 | 125.0 | 1.000000 | 2.0 |
データフレームの解説 1列目と2列目:結合されたクラスターの番号 3列目:クラスター間の距離 4列目:結合後に新しくできたクラスタの中に入っている元のデータの数
ここでウォード法を使っています。
ウォード法は、クラスタ同士が結合すると仮定した時、結合後の全てのクラスタにおいて、クラスタの重心とクラスタ内の各点の距離の平方和の合計が最小となるように、クラスタを結合させていく方法でした。
階層型クラスタリングの一種で、クラスタ間の距離を最小化するようにクラスタを結合します。
具体的には、ウォード法はクラスタ間の距離を、クラスターを結合したときに生じる全体の平方和の増加量\(ΔSS(C, C’)\)と定義します。
これは、クラスタ内のデータポイントがクラスタの中心からどれだけ離れているかを測定することで、クラスタ内のばらつきを最小化することを目指しています。
$$ΔSS(C, C’) = \frac{|C|×|C’|}{|C|+|C’|} × d(C, C’)^2$$
\(|C|\)と\(|C’|\)はそれぞれクラスタ\(C\)と\(C’\)のデータポイントの数を表します。
\(d(C, C’)\)はクラスタCとC’の中心間のユークリッド距離を表します。
この\(ΔSS(C, C’)\)が最小となるクラスタのペアを見つけ、それらを結合することを繰り返します。
このプロセスは、指定されたクラスタ数に達するまで、または全てのデータポイントが1つのクラスタに結合されるまで続けられます。
補論:ウォード法を使うときに、データは正規分布に従うべき?
ウォード法で使う、全体の平方和の増加量にはデータが正規分布に従っていることは仮定されていません。
ただ、ウォード法が特に正規分布に従うデータに対して有効です。
その理由は、クラスタ内の平方和(つまり、クラスタ内の分散)を最小化することを目指しているからです。
正規分布は、その特性上、データの大部分が平均値(つまり、クラスタの中心)の近くに集中しています。
したがって、正規分布に従うデータに対してウォード法を適用すると、自然にクラスタ内の分散が最小化され、より「密集した」クラスタが形成される傾向があります。
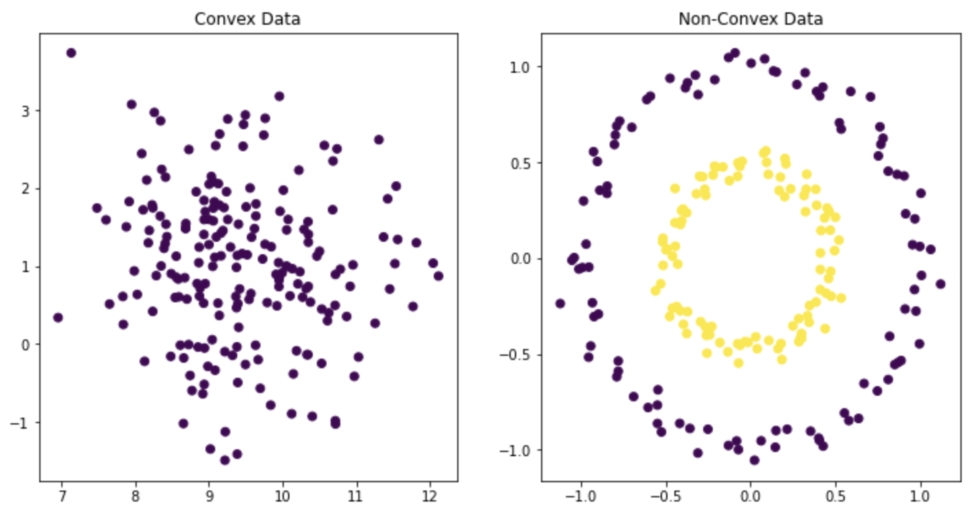
クラスタ内の分散を最小化することを目指している以上、データが凸型(Convex)(下図左)になることを前提としており、クラスタの形が非凸型(Non-Convex)(下図右)のデータなどはDBSCANやスペクトラルクラスタリングによる分類を検討することが良いでしょう。
デンドログラム
#デンドログラム
#視覚的にどうクラスターを分けたかわかる。
from scipy.cluster.hierarchy import dendrogram
import matplotlib.pyplot as plt
fig2,ax2 = plt.subplots(figsize=(20,5))
ax2 = dendrogram(Z)
fig2.show()
このように樹形図でクラスター分けの様子が見れます。
赤、緑、黄色の3色であり、3つのクラスターに分けてくれたことがわかります。
また、距離水準を3よりも大きく取るともっと細かくクラスター分けすることも可能であり、クラスター数を柔軟に決定することができます。
from scipy.cluster.hierarchy import fcluster
clusters = fcluster(Z,t=3,criterion="maxclust")
for i,c in enumerate(clusters):
print(i,c)最後に、どの生徒がどのクラスターに分けられたのかを見てみましょう。
0 3 1 3 2 3 3 2 4 2 5 2 6 3 7 3 8 3 9 2 ‥
以上が出力結果です。これが縦に人数分続く形になっています。
さて、ここまで技術と国語のテストの点数を指標にして生徒をクラスターに分けると、3つが「ちょうどいい」というのが教師なし機械学習の提案です。

実際の業務では、「なぜこの分類になったのか」「このクラスターの購買行動は○○だから、アプローチCをとってみよう」的な「分析の先の打ち手の提案」が必須になります。
分析結果をしっかりとドメイン知識に基づいて解釈して、いい打ち手に繋げられるようになりたいですね。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!





