【最短合格】統計検定準一級のチートシート|難易度や出題範囲について
こんにちは、青の統計学です。
今回は、統計検定準一級のチートシートをご紹介します。
第二弾はこちら→【第2弾】統計検定準1級のチートシート｜最短合格への道
統計検定2級はこちら→【最短】統計検定2級合格ロードマップとチートシート
確率分布のモーメント母関数についての導出チートシートは以下のコンテンツをご覧ください。
こちらでも個別のコンテンツをピックアップしております。より網羅的に学習したい方はこちらをご覧ください。
統計検定準一級の範囲と難易度
一旦統計検定準一級の範囲をご紹介します。
2級よりも範囲が広く内容も難しいです。準一級の壁は個人的に高いと思っています。
| 基礎統計学 | 記述統計 ,確率と確率分布,推測統計, |
| 多変量解析 | 主成分分析,判別分析,因子分析,クラスタ分析, |
| 時系列解析 | 時系列データの特性,ARMAモデル, |
| 実験計画法 | 一般的な実験の計画と分析,分散分析,因子計画 |
| 生存時間解析 | ハザード関数と生存関数,カプラン-マイヤー推定 ,コックス比例ハザードモデル |
| 線形モデル | 単回帰分析,重回帰分析 ,一般化線形モデル |
| ノンパラメトリック | 順位データの分析,散布図と相関 |
| ベイズ統計 | ベイズの定理,事前分布と事後分布,ベイズ的モデル選択 |
| シミュレーション | モンテカルロ法 ,確率的シミュレーション |
確率過程や因子分析が対策後回しにしがちになるので、出題されると痛いです。
実験計画法分野のチートシート
分散分析について
ここでは残差平方和、水準間平方和、F値の求め方をまとめております。
それぞれの自由度に関しては、
水準の自由度：水準数-1
全体の自由度：サンプル数-1
残差の自由度：全体の自由度-水準の自由度
ちなみに、AとBという水準がある場合、大抵A×Bという交互作用の水準もできますが、交互作用の自由度はAの自由度とBの自由度の積です。
水準と残差の分散(水準間平均平方和や残差平均平方和などと呼ばれるケースもあります)は、それぞれの平方和を自由度で割ってあげると算出できます。
ちなみに母分散の不偏推定量は、残差平均平方和と一致します。
$$SSB = \sum_{i=1}^{k} n_i (\bar{X}_i – \bar{X})^2$$
$$SSW = \sum_{i=1}^{k} \sum_{j=1}^{n_i} (X_{ij} – \bar{X}_i)^2$$
$$F value = \frac{\frac{SSB}{v_{B}}}{\frac{SSW}{v_w}}$$
水準間平方和は、各水準の平均と全体平均の差をとり2乗→各水準のサンプル数で掛けた和ですね。
残差平方和は、各水準のデータと各水準の平均の差をとり、平方和を取り→水準間でも和をとる、ですね。
F値は、水準の分散を残差の分散で割った値です。これをF検定につかい、棄却限界値との大小比較に使います。
交互作用になろうが水準が幾つに増えようが、分母は残差の分散になります。
分散分析については、統計検定2級から出題されている定番テーマです。
F値まできちんと求めて正解しておきたいところです。
【F値とは】分散分析による検定の多重性について|統計検定準1級
【統計検定2級で最も手強い(主観)】分散分析について解説します①
点推定値の95%信頼区間について
水準Aの平均値を使って、信頼区間を作ることもできます。
$$\overline{A}±t_{α/2,df}\sqrt{\frac{SSW}{n_A}}$$
ただしt分布の自由度は残差の自由度になります。
標準誤差の方は母分散の不偏推定量を水準のサンプル数で割り、根号をつけます。
標準誤差の定義が怪しい方は今一度、下記コンテンツを見返しててください。
また検定の多重性に関しては、ボンフェローニの補正やturkeyの補正までわかるとバッチリです。
【F値とは】分散分析による検定の多重性について|統計検定準1級
回帰分析分野のチートシート
基礎的な内容は、こちらをどうぞ！
ロジスティック回帰の計算周りについて
さて、ロジスティック関数の式が与えられた時、適切にオッズや対数オッズなどが求められるでしょうか？
これを機に覚えておきましょう！
以下は詳細記事です。
$$z=β_0+\sum_{i=0}^{h}β_iX_i+ε$$
こちらのロジット関数のzが対数オッズになります。
つまり、\(log\frac{\hat{π}}{1-\hat{π}}=z\)です。
さて、では対数を外してオッズを求めてみましょう。
$$\frac{\hat{π}}{1-\hat{π}}=e^{β_0}+\sum_{i=1}^{h}(e^{β_{i}})^{X_k}$$
では肝心の確率の求め方は以下になります。
$$\hat{π}=\frac{e^z}{1+e^z}$$
こちらはNNでもよくみられるシグモイド関数形ですね。
偏相関係数について
偏相関係数とは、xとyの相関を求める際に他の変数zの影響を取り除いた相関係数です。
複数の変数が関与する場面で、特定の2つの変数間の純粋な関係性を評価したい場合に偏相関係数を使用します。
例えば、年齢、収入、教育レベルなど、複数の変数がある場面で、年齢と収入の関係性を、教育レベルの影響を取り除いて評価したい場合などに使用します。
$$r_{xy|z}=\frac{r_{xy}-r_{xz}*r_{yz}}{\sqrt{1-r_{xz}}\sqrt{1-r_{yz}}}$$
普通の相関係数と偏相関係数に大きな差がある場合に、他の変数による交絡があると言えますね。
多重共線性や操作変数法などの議論に繋がります。因果まではわからないですが、実務でもよく使う指標です。
【論文解説】多重共線性は回帰分析にどのような影響を与えるのか
生存時間解析について
生存関数\(S(t)\)とハザード関数の関係や、指数分布を例にとった確率密度関数の求め方などを解説します。
まず、\(S(t)\)を生存関数とおいた時、ハザード関数は以下のように表し、時刻tにおいて生存しているもののうち、その後短時間で死亡するものの率を示します。
$$h(t)=\frac{f(t)}{1-F(t)}=(-logS(t))’$$
ここで\(F(x)\)は確率分布関数、\(f(x)\)は確率密度関数を表します。
もし、\(S(t)=P(T≧t)=exp(-λt)\)のような形で表せる場合、累積分布関数は以下のように1との差で表すことができます。
$$1-exp(-λt),(t≧0)$$
この累積分布関数を時刻tについて微分すると、確率変数Tの確率密度関数が得られます。
$$f(t)=λexp(-λt),(t≧0)$$
さて、密度関数が求められたとのことで期待値について求めてみましょう。
$$E[f(t)]=\int λexp(-λt)dt$$
高校数学で習った部分積分を使ってみましょう。
$$\int_{0}^{∞}t(-e^{-λt})dt-\int_{0}^{∞}(-e^{-λt})dt$$
$$0-0-[-\frac{e^{-λt}}{λ}]_{0}^{∞}=\frac{1}{λ}$$
よって、期待値はハザード率の逆数であることがわかりました。
さて、今回は指数分布をご紹介しました。
指数分布は一つの基本的なモデルとして使われますが、それが常に最も適切なモデルであるわけではありません。
指数分布は、イベントが発生する確率が時間の経過とともに一定である（メモリレス性）場合に当てはまります。
言い換えると、あるイベントがまだ発生していない時間tまでの生存時間がどれだけ長くても、次の瞬間にそのイベントが発生する確率は一定です。
しかし、多くの実際の現象では、時間の経過とともにイベントが発生する確率が増加するか、または減少することがあります。
このような場合、他の分布（例えばワイブル分布やロジスティック分布など）が指数分布よりも適切である可能性があります。
ワイブル分布の場合、確率密度関数は\(f(t)=λp(λt)^{p-1}e^{-(λt)^p}\)となり、指数分布の一般系を表します。
pと1との大小関係によって、ハザードが単調増加か単調減少か変わります。
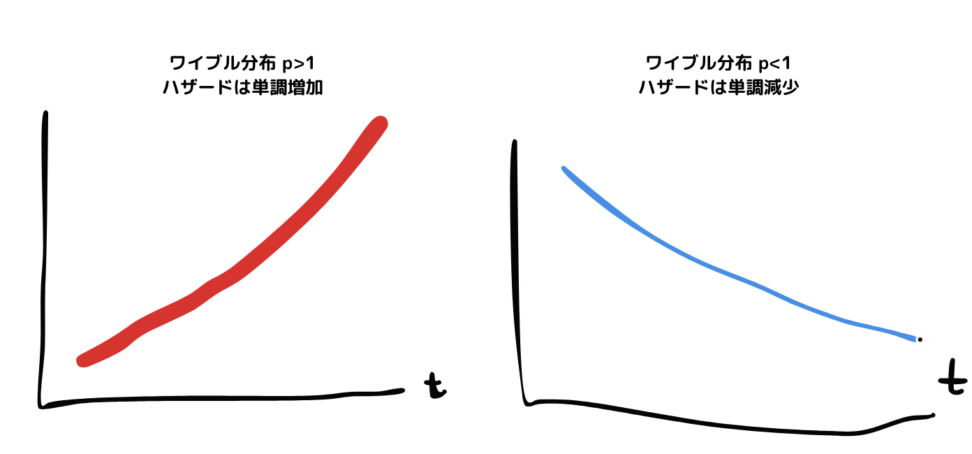
中央値を求めたい場合は？
中央値や四分位を求めたい場合は、生存関数の方を使います。
$$S(t)=\frac{1}{2}$$
仮説検定分野のチートシート
独立性の検定のオッズ比と標準誤差について
男性と女性によって、新薬の投与による効果に違いがあるかを知りたいとしましょう。
| 男性 | 女性 | ||
| 介入群 | a | b | a+b |
| コントロール群 | c | d | c+d |
| a+c | b+d | a+b+c+d |
介入のオッズ比は以下のように表すことができます。
$$OR=\frac{\frac{a}{b}}{\frac{c}{d}}=\frac{ad}{bc}$$
それぞれの理論値を\(a*\)のように表すとすると、対数オッズ比の標準誤差は以下のように表すことができます。
$$SE(lnOR)=\sqrt{\frac{1}{a*}+\frac{1}{b*}+\frac{1}{c*}+\frac{1}{d*}}$$
よって、オッズ比の95%信頼区間は、以下のように表すことができます。
Zは、信頼区間に対応する正規分布のパーセンタイルです。
95%信頼区間の場合、 Zは1.96です。間違えてカイ２乗分布の3.84をかけないようにしましょう。
$$log(OR)±Z×SE(ln(OR))$$
また、この時のカイ二乗統計量は、以下のように表すことができます。
一般に独立性の仮説(帰無仮説)のもとでの期待度数\(m_{ij}\)は\(E_{ij}=\frac{合計行iの度数×合計列jの度数}{全体の度数}\)と表せます。
$$χ^2=\sum\frac{x_{ij}-m_{ij}}{m_{ij}}$$
また、独立性の検定に関する逸脱度Gは以下のように表すことができます。
$$G^2=2\sum x_{ij}log\frac{x_{ij}}{m_{ij}}$$
この逸脱度がカイ二乗統計量と同様に独立性を検定するために使用されることがあり、データが期待度数に従っている場合、この統計量はカイ二乗分布に従うと期待されます。
さて、逸脱度と聞いて最大対数尤度とモデルの対数尤度の差に2をかけるものもあります。
【python】尤度比検定で統計モデルの比較をしよう|統計的仮説検定
2つの定義は、異なる目的のために逸脱度が計算されるため、異なります。
GLMの文脈での逸脱度は、モデルの適合度の評価に特化しているのに対し、今回の独立性の検定の文脈での逸脱度は、観測データと期待データの間の相違を評価するために使用されます。
上の統計量と逸脱度の自由度は、行数と列数に基づいて計算されます。
もし r行c 列のクロス表（分割表）がある場合、自由度 df は以下のように計算されます
$$df=(r-1)×(c-1)$$
2項分布周りの信頼区間や検定統計量など
コイン投げの表裏や男女のサービス利用率、発病したか否かなど、問題を作りやすい2項分布周りのチートシートになります。
確率\(p_i\)で事象\(A_i\)が起きる試行を\(n\)回行う場合、確率変数\(X_i\)は二項分布に従います。
以下のような期待値と分散を持ちます。
$$E(X_i)=np_{i},V(X_i)=np_i(1-p_i)$$
また、点推定値が\(\hat{p}_i\)の場合、95%信頼区間は以下のように表すことができます。
$$\hat{p}_i±1.96×\sqrt{\frac{\hat{p}_i(1-\hat{p}_i)}{n}}$$
二項分布の信頼区間を考える際の標準誤差は、二項分布の標準偏差に基づきます。
二項分布の標準偏差は、\(\sqrt{n×p×(1-p)}\)であり、信頼区間を計算する際の標準誤差は、この標準偏差を観測数 \(n\)の平方根で割ったものになるので、上のようになります。
標準誤差について復習したい方は以下のコンテンツをご覧ください。
また、棄却限界域を求める際の検定統計量は以下のように表すことができます。
$$P(\frac{\hat{p}-p_{H0}}{\sqrt{\frac{p_{H0}(1-p_{H0})}{n}}}≧c)$$
母比率の差の検定について
インスタグラムの利用率について、男女で差があるのかという問題が出ましたね。
まず点推定値の信頼区間の求め方については以下のようになります。
$$\hat{θ}_{1}-\hat{θ}_{2}±Z_{α/2}\sqrt{\frac{\hat{θ}_{1}(1-\hat{θ}_{1})}{n_1}+\frac{\hat{θ}_{2}(1-\hat{θ}_{2})}{n_2}}$$
母比率の差についての仮説検定で使う統計量は以下のようになります。
正規分布の再生性を使っていますね。
$$\frac{\hat{θ}_1-\hat{θ}_2}{\sqrt{(\frac{1}{n_1}+\frac{1}{n_2})\hat{θ*}(1-\hat{θ*})}}$$
検出力と有意水準指定によるサンプルサイズ設計について
次は検出力80%や有意水準5%と指定された場合に必要なサンプルサイズの求め方について求めて行きます。
検出力については説明を省きますが、詳しくは以下のコンテンツをご覧ください。
まずは、以下のような具体例を見てみましょう。
[2群の平均の差の検定] 投薬による血圧減少量を知りたいとして、新薬群の期待値をμ_a,プラセボ群の期待値をu_pとします。 H0:μ_a=μ_p H1:μ_A-μ_P=δ>0 上のような仮説の置き方になります。 ・有意水準5%で有意 ・検出力は80%を担保 したいときに必要なサンプルサイズを求めたいです。 前提：それぞれの群のサンプルサイズは同じで、どちらも分散σ^2の正規分布に従う
まず2群の平均値の差がどのような分布に従うのかをみた方が良いですね。
帰無仮説が正しいと仮定すると、当然期待値は0です。
一方で対立仮説が正しいとすると、期待値は問題通り\(δ\)となります。
また、分散は分散の加法性より\(\frac{2σ^2}{n}\)ですね。
＊ちなみに同じ分布に従う\(μ_A\)と\(μ_P\)の差なんだから、当然正規分布に従うだろと思うかもしれませんが、これは「再生性」という正規分布の性質があるからです。
必ずしも同じ分布になるとは限らないので、覚えておきましょう。
ポアソン分布とかも再生性があります。
ポアソン分布について詳しく知りたい方は、以下のコンテンツをご覧ください。
さて分散がわかったところで検定統計量を作りましょう。
実現値\(δ\)を標準偏差で割ります。
$$\frac{δ}{\frac{2σ^2}{n}}$$
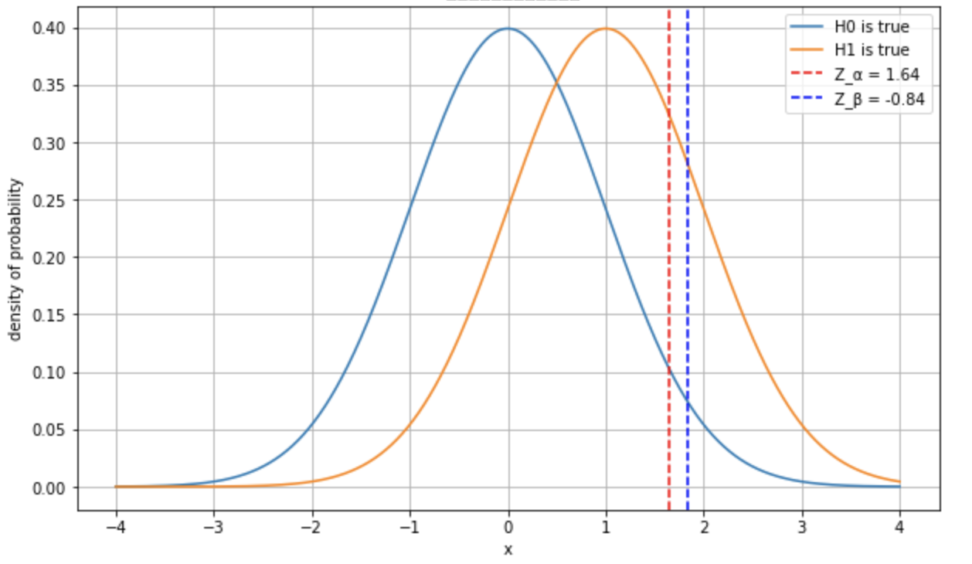
また、片側検定の場合、\(Z_α\)と\(Z_β\)の値は、通常の正規分布のパーセンタイルから求められます。
片側5%の棄却限界域と検出力80%より、\(z_α=1.64\)で\(z_β=0.84\)ですね。
仮説検定の文脈で考えると、\(Z_α\)は第一種の過誤のリスクを制御するための閾値を、\(Z_β\)は検出力を制御するための閾値を示しています。
以下がチートシートポイントです。
サンプルサイズの計算式を導出するため、まず、次のような等式を考えます。
$$\frac{δ}{\frac{2σ^2}{n}}-Z_β=Z_α$$
$$δ-\frac{2σ^2}{n}*Z_β=Z_α*\frac{2σ^2}{n}$$
なぜこのような形になるかというと、
この式は、差\(δ\)が実際に存在する場合(H1)の分布の平均\(δ\)から\(Z_β\)だけ左にずれた位置が、差が0のとき(H0)の分布の平均から\(Z_α\)だけ右にずれた位置と一致するという意味を持っています。
つまり検出力は対立仮説が正しいと仮定し、有意水準では帰無仮説が正しいと仮定しているのです。
計算を続けます。
$$δ=(Z_α+Z_β)*\frac{2σ^2}{n}$$
$$n=2σ^2×(\frac{(Z_α+Z_β)}{δ})^2$$
因子分析についてのチートシート
バリマックス回転
因子負荷量の解釈をし易くするように、因子負荷行列の各要素の2乗の分散の和を最大にする回転方法です。
具体的には、ある因子負荷行列\(P\)が存在するとき、この行列を回転させるためには、適切な回転行列\(T\)を使って新しい因子負荷行列\(P′\)を得ます。
この操作は以下のような数式で表すことができます
$$P’=P×T$$
この回転により、各因子でいくつかの因子負荷の絶対値は1にに近づき、それ以外の因子負荷量は0に近づく傾向になります。
共通性について
共通因子には、独自性と共通性があり、値を求める問題が出ます。
因子負荷量が与えられた場合、共通性は\(\alpha_{i}^2\)と表すことができます。
$$1=α{i}^2+d_{i}^2$$
このように因子負荷量と独自係数の平方和は1になることを利用し、因子負荷量を使って独自性まで求めることができます。
確率過程分野のチートシート
ブラウン運動の増分について
独立なブラウン運動の差分の積の期待値は0になることを覚えていただきたいです。
\(B_t-B_s〜N(0,t-s)\)ということになります。
増分が正規分布に従うということですね。
以下のようなブラウン運動1,2,3に基づく確率過程が二つあるとします。
$$x_t=x_0+σ_1\sqrt{ρ}B_t^{1}+σ_1\sqrt{1-ρ}B_t^{2}$$
$$y_t=y_0+σ_2\sqrt{ρ}B_t^{1}+σ_2\sqrt{1-ρ}B_t^{3}$$
ブラウン運動に基づく2つの確率過程 \(x_t\)と \(y_t\)を考える時、それぞれの差分は次のように書けます
$$Δx_k = x_{\frac{k}{10}} – x_{\frac{k-1}{10}}$$
$$Δy_k = y_{\frac{k}{10}} – y_{\frac{k-1}{10}}$$
では、この差分の積の期待値\(E[Δx_kΔy_k]\)を求めてみましょう。
この期待値の中で、独立なブラウン運動の差分の積の期待値は0になるので
$$E[ΔB_t^{(1)}B_t^{(2)}]=0$$
$$E[ΔB_t^{(1)}B_t^{(3)}]=0$$
このようになります。
一方、同じブラウン運動の差分の期待値は、以下のように非ゼロです。
$$E[ΔB_t^{(1)}B_t^{(1)}]=Δt$$
したがって、積の期待値の非ゼロの部分は次の部分だけです
$$E[Δx_kΔy_k]=σ_1σ_2ρE[ΔB_t^{(1)}B_t^{(1)}]$$
この場合、\(Δt = \frac{1}{10}\) ですので答えは以下のようになります。
$$E[Δx_kΔy_k]=\frac{σ_1σ_2ρ}{10}$$
ブラウン運動（またはWiener過程）は確率過程の一つであり、特に連続時間の確率モデルにおいて頻繁に用いられます。
今回の独立なブラウン運動の積の期待値は0になるという特性以外にも、さまざまな性質があります。
以下にブラウン運動の主な特徴を挙げておきます。
開始地点: \(B(0)=0\)すなわち、時刻\(0\)におけるブラウン運動の値は\(0\)です。
連続性: ブラウン運動はすべての時刻で連続です。
独立性: ある時間間隔における増加分は、別の非重複の時間間隔における増加分と独立です。
正規分布の増分: ある固定の時間間隔、例えば \(t\)と \(t+Δt\)の間の増分、\(B(t+Δt)−B(t)\)は平均が0で分散が\(Δt\)の正規分布に従います。
時刻間の独立性: \(s<t\)に対して、 \(B(t)−B(s)\)は \(B(s)\) と独立です。
再び正規分布: ブラウン運動の増分は、その期間によらず、平均\(0\)の正規分布に従います。
中でもブラウン運動\(B_t\)の周辺分布、つまり増分の和は中心極限定理により、\(N(0,t)\)に従います。
確率過程については、以下のコンテンツでも取り上げております。
ポアソン過程に従う時間tまでのイベント数の期待値の求め方について
強度(生起率とも言いますね)λのポアソン過程に従う時間tまでのイベント数\(X_t\)の期待値を求めたいです。
覚えてしまっても良いかもしれませんが、答えは\(\lambda t\)です。
$$E[X_t]=\sum_{n=0}^{∞}ne^{-λt}\frac{(λt)^n}{n!}$$
無限等比級数の一部である、\(n\frac{(λt)^n}{n!}\)は\(e^{λt}\)のテイラー展開\(e^{λt}=\sum\frac{(λt)^n}{n!}\)の微分形です。
$$E[X_{t}]=e^{-λt}×λt×e^{λ}=λt$$
統計検定準一級の実際の問題だと、誤植発見率qが適用され期待値がλqtとなっていましたね。
イベントの発生したとしても、それを発見する確率も関わるという一段応用が効いた問題でした。
ポアソン過程については以下をご覧ください。
複合ポアソン過程周りの分散について
複合ポアソン過程の分散まで知っておくと良いでしょう。
複合ポアソン過程を考える際、基本となるポアソン過程の発生回数を\(N_t\)とし、\(X_t=\sum_{i=1}^{N_t}U_i\)とした時、時刻tまでの観測数を\(X_t\)になります。
確率qで観測するとします。
そして、\(U_k\)は独立にベルヌーイ分布に従うことにしましょう。
なので、\(E[U_i]\)=qおよび\(V(U_i)=q(1-q)\)が成立しますね。
ここで、\(X_t\)の分散を求めたいとします。
$$V (X_t) = E[X_{t}^2] − E[X_{t}]^2$$
これは普通に分散の性質です。この公式を整理すると以下のように和の形にできます。
$$E[X_{t}^2] = E[X_{t}]^2 +V(X_{t})$$
では、\(N_t\)という条件付きの形に落とし込みましょう。
$$E[X_{t}|N_t]^2 = E[X_{t}|N_t]^2 +V(X_{t}|N_t)$$
では、繰り返し期待値の法則\(E[Y]=E[E[Y|X]]\)を使ってみましょう。
$$E[X_{t}^2]= E[E[X_{t}^2|N_t] +V(X_{t}|N_t)]=E[E[X_{t}^2|N_t]] +E[V(X_{t}|N_t)]$$
$$V(X_{t})= E[V(X_{t}|N_t)]+E[E[X_{t}^2|N_t]]-E[E[X_{t}|N_t]^2]$$
$$V(X_{t})= E[V(X_{t}|N_t)]+E[V(X_{t}|N_t]]=E[N_t×V(U_i)]+E[N_t×V(U_i)]$$
$$V(X_{t})=E[N_t]×V(U_i)+E[N_t]^2×V(U_i)=λt×q(1-q)+q^2×λt=λqt$$
分散はλqtとなりました。期待値と一緒ですね。
