【F値とは】分散分析による検定の多重性について|統計検定準1級
統計検定準一級では、2級同様「分散分析」の内容が出てきます。
今回は、前回と視点を変えた「検定の多重性」について解説します。
例題を通して理解していきましょう。
*確実に理解するために、ある程度時間をかけてみましょう。
分散分析の基礎から学習したい方は、以下のコンテンツをご覧ください。
【統計検定2級で最も手強い(主観)】分散分析について解説します①
検定の多重性とは
ある自動車会社Xは、自動車の色と事故率の関係について調査を始めました。 X社が販売している車の色は全部で赤/青/黒/白の4種類です。 今回は、車の色を水準とし、販売した車の事故率を確かめた。各水準の繰り返し数(ni)(i=1,2,3,4)は一定ではありません。
| 車の色 | ni | 1回目 | 2回目 | 3回目 | 4回目 | 5回目 | 平均 |
| C1(赤) | 5 | 3.4 | 3.1 | 2.9 | 2.8 | 2.7 | 2.98 |
| C2(青) | 4 | 2.5 | 2.8 | 3.0 | 2.8 | / | 2.78 |
| C3(黒) | 5 | 3.2 | 3.1 | 3.0 | 3.1 | 2.8 | 3.04 |
| C4(白) | 4 | 3.3 | 3.2 | 2.9 | 3.4 | / | 3.20 |
| 計 | 18 | / | / | / | / | / | 3.0 |
以下の一元配置分散分析モデルを作ります。
ただし、
・εは誤差項。\(ε〜N(0,σ^2)\)
・iは試行回数(1〜5)
・jは車の色(1〜4)
・\(μ_i\)は母平均
とします。
\(y_{ij}\)は観測データとし、\(Y_{ij}\)は、確率変数の実現値です。
$$Y_{ij}=μ_{i}+ε_{ij}=μ+α_{i}+ε_{ij}$$
(1)以下の帰無仮説と対立仮説を考えます。
\(H0\)：母数\(α_j=0\)
(訳：全ての水準に関して、事故率に対する影響がない)
\(H1\)：少なくとも一つの母数が異なる。
分散分析表を作り、母分散\(σ^2\)の不偏推定量を求めてみましょう。
さらに5%有意水準のF検定を行いましょう。
＊ちなみに、分散とは「水準間平均平方和」と「残差平均平方和」のことです。
| 要因 | 平方和 | 自由度 | 分散 | F値 |
| 色(水準) | ? | ? | ? | ? |
| 誤差 | ? | ? | ? | / |
| 合計 | ? | ? | / | / |
(2)ある研究者は、各色のうちどの色の間に有意な差があるのか、有意水準5%で検定を行うことにしました。
しかし、検定の多重性を回避するために、5%よりも厳しい有意水準を設定する「ボンフェローニ補正」を行いました。
この例題において、ボンフェローニ補正を行うときの有意水準を答えてください。
【解説】
(1)統計検定準一級を目指す方なら、基礎的な分散分析表は作れて当然でしょう。
2群、2グループの平均の比較はt検定で、3群・3グループ以上の平均の比較は分散分析でした。
一元配置分散分析の仮説検定のやり方は頻出です。
「母数を全て0にする」帰無仮説vs「少なくとも1つの母数は値が異なる。」対立仮説です。難易度が上がってもここは変わりません。
まずは、自由度を求めてみましょう。
自由度
これは前回の記事でも勉強しました。
水準間の自由度は、水準のサンプル数から1を引いたもの。水準は色なので4-1で3ですね。
全体の自由度は、行数×列数-1です。
注意してほしいのは、試行回数が水準によって異なることです。
この場合は、大雑把に行数×列数をしてはいけません。有効なセルの数を足し合わせましょう。5+4+5+4-1で17です。
残差の自由度は、全体の自由度から水準間の自由度を除いたものです。17-3で14です。
| 要因 | 平方和 | 自由度 | 分散 | F値 |
| 色(水準) | 3 | |||
| 誤差 | 14 | / | ||
| 合計 | 17 | / | / |
自由度が全て埋まりました。次は、水準間平方和と残差平方和を求めていきましょう。
水準間平方和
水準間平方和を求めるにあたって、分散分析を行う目的を考えましょう。
「色(水準)による車の事故率の違いを知りたい」
でした。
まず全体の事故率の平均を求めた上で、各水準の事故率の平均を引いてみましょう。
全体の事故率の平均は、表の右下を見ればわかります。3.0です。
各水準の平均と全体の平均の差を取ります。後で平方するので、マイナスでも良いです。
水準C1と全体の差：3.0 – 2.98 = 0.02
水準C2と全体の差：3.0 – 2.78 = 0.22
水準C3と全体の差：3.04 – 3.0 = 0.04
水準C4と全体の差：3.20 – 3.0 = 0.2
では平方和をとりましょう。ちゃんと試行回数をかけることを忘れないようにしましょう。
0.0004 × 5 + 0.484 × 4 + 0.0016 × 5 + 0.04 × 4 = 2.106
残差平方和
残差平方和は、各水準の平方和の和です。
C!ならC1の平均から各試行の事故率を引き、平方和をとります。要は偏差の平方和です。
C4まで行い、全ての和をとった値が残差平方和です。
水準(色による)による違いを除いた違いを表しています。
C1の残差平方和：\((3.4 – 2.98)^2 + (3.1 – 2.98)^2 + (2.9 – 2.98)^2 + (2.7 – 2.98)^2 +(2.98 – 2.7)^2= 0.354\)
C2の残差平方和：\((2.78 – 2.5)^2 + (2.78 – 2.8)^2 + (2.78 – 3.0)^2 + (2.78 – 2.8)^2 = 0.1276\)
C3の残差平方和：\((3.04 – 3.2)^2 + (3.04 – 3.1)^2 + (3.04 – 3.0)^2 + (3.04 – 3.1)^2 + (3.04 – 2.8)^2 = 0.092\)
C4の残差平方和：\((3.2 – 3.3)^2 + (3.2 – 3.2)^2 + (3.2 – 2.9)^2 + (3.2 – 3.4)^2 = 0.14\)
全体の平方和：\(0.354 + 0.1276 + 0.092 + 0.14 = 0.7136\)
| 要因 | 平方和 | 自由度 | 分散 | F値 |
| 色(水準) | 2.106 | 3 | ||
| 誤差 | 0.7136 | 14 | / | |
| 合計 | 2.8196 | 17 | / | / |
ここまでで、水準間平方和と残差平方和がもとまりました。
F値と分散は一気に求めましょう。ここでいう「分散」は水準間平均平方和と残差平均平方和のことです。
F値
F値は、水準間平均平方和を、残差平均平方和で割った値です。
それぞれの平均平方和は、データ数で割るのではなく、自由度で割ります。
よって、以下のようになります。
$$Fvalue = \frac{水準間平均平方和}{残差平均平方和}=\frac{\frac{2.106}{3}}{\frac{0.7136}{14}}=13.77$$
回帰分析の文脈で言えば、F値は説明変数のうち少なくとも一つが目的変数の役にたつかどうかを判定するための指標です。
一方、t値は個々の説明変数がいるかいらないかを判断するための指標です。
F値は、書き換えると以下のように表せます。
$$F value = \frac{n-p-1}{p}\frac{R^2}{1-R^2}$$
もし全ての説明変数が不要、すなわち\(β_1=β_2,…,β_p=0\)であったならば、Fは自由度p,n-p-1のF分布に従うことが知られています。
分散分析表が完成しました。
| 要因 | 平方和 | 自由度 | 分散 | F値 |
| 色(水準) | 2.106 | 3 | 0.702 | 13.77 |
| 残差 | 0.7136 | 14 | 0.05097143 | / |
| 合計 | 2.8196 | 17 | / | / |
【重要】また、母分散の不偏推定量は「残差平均平方和」と一致します。
計算手順を見れば、当たり前と言う感じですが、名前が違うと別物と考えてしまいがちです。
では、検定してみましょう。
F値は13.77で、第一自由度は3で第二自由度は14でした。
α=0.05のF分布表を見ると、F(3,15)が一番近いですね。8.7029です。
F 値 13.77 > F(3.14)なので、「帰無仮説は棄却されます」
つまり、事故率の差に車の色の影響はあるということがわかりました。
| α＝0.05 | 10 | 12 | 15 | 20 | 24 | 30 | 60 | 120 |
| 2 | 19.3959 | 19.4125 | 19.4291 | 19.4458 | 19.4541 | 19.4624 | 19.4791 | 19.4874 |
| 3 | 8.7855 | 8.7446 | 8.7029 | 8.6602 | 8.6385 | 8.6166 | 8.5720 | 8.5493 |
| 4 | 5.9644 | 5.9117 | 5.8578 | 5.8025 | 5.7744 | 5.7459 | 5.6877 | 5.6581 |
| 5 | 4.7351 | 4.6777 | 4.6188 | 4.5581 | 4.5272 | 4.4957 | 4.4314 | 4.3985 |
| 6 | 4.0600 | 3.9999 | 3.9381 | 3.8742 | 3.8415 | 3.8082 | 3.7398 | 3.7047 |
| 7 | 3.6365 | 3.5747 | 3.5107 | 3.4445 | 3.4105 | 3.3758 | 3.3043 | 3.2674 |
| 8 | 3.3472 | 3.2839 | 3.2184 | 3.1503 | 3.1152 | 3.0794 | 3.0053 | 2.9669 |
| 9 | 3.1373 | 3.0729 | 3.0061 | 2.9365 | 2.9005 | 2.8637 | 2.7872 | 2.7475 |
| 10 | 2.9782 | 2.9130 | 2.8450 | 2.7740 | 2.7372 | 2.6996 | 2.6211 | 2.5801 |
検定の多重性
検定の多重性とは、その名の通り統計的検定を複数回行うことによって起きる問題です。
そして、具体的にどのような問題かというと、
少なくとも一つの検定が有意になる確率が上がってしまう
ということです。問題の解説を通して理解してみましょう。
(2)
分散分析は、どの水準とどの水準の間の差に有意差があるのかわからないです。
【重要】(1)で調べたのは、「どの水準にも差はないのでしょうか？」という仮説が否定されて、「水準間に差はあります。ただし、どの水準とどの水準の間の差が有意かまでは分からないです。」というところまでです。
では、実際に水準のうち2つを選んでt検定をしていき、有意差を探していくのが、
「多重比較」
であり、検定の多重性という問題が生まれるところでもあります。
先ほど説明した検定の多重性の問題点を、例に沿って説明します。
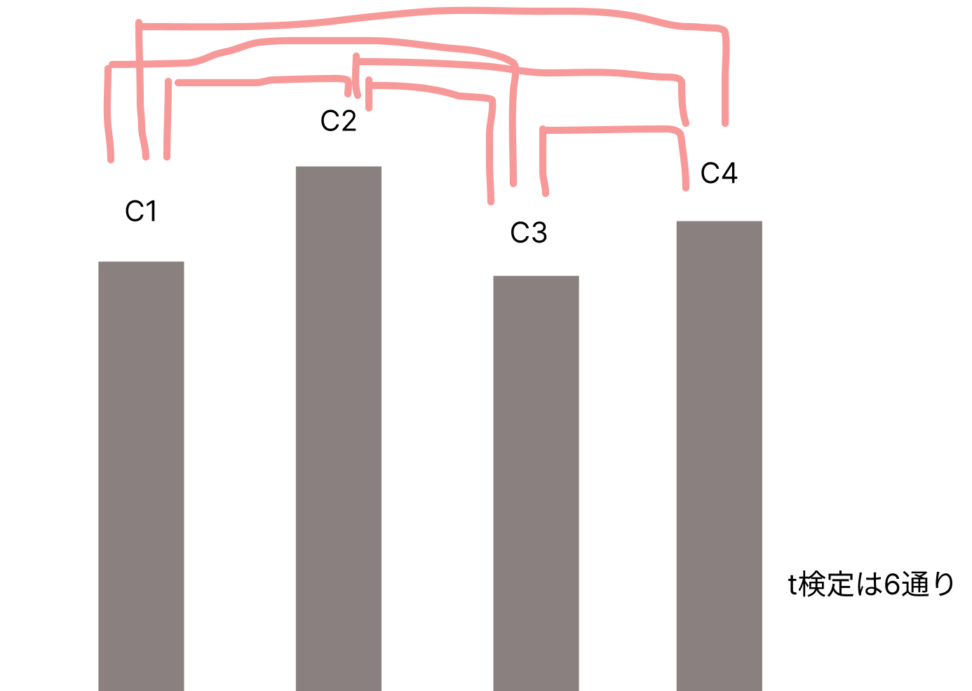
6回連続で有意水準5%で、t検定をやってしまう
→少なくとも1つの組み合わせが有意になる確率は6倍になる。
→6×5%有意水準で1回t検定をやっているようなもの。有意差が出やすい。
こういった落とし穴は割と存在していて、例えばクラスタリングをした後の群にANOVA等の検定をかけると、クラスタリングをした時点で傾向が違う群を取り出しているので、有意になりやすいなど、実験計画自体に細心の注意が必要なのです。
機械学習における多重検定について
分散分析以外でも多重検定の問題はあります。
スパースなデータ(Yに相関が無い、ノイズを大量に投入したような高次元のデータ)を扱う際に、特徴量を削除せずにモデルを作成すると
それぞれの回帰係数は有意になりやすいです。
これは多重検定の問題です。
それぞれの回帰係数に一つずつ適用する局所的なp値に対して、データ全体で有意かどうかを考える大局的なF値を参考にすると良いでしょう。
$$F = \frac{\frac{TSS-RSS}{p}}{\frac{RSS}{n-k-1}}$$
TSSは全変動と呼ばれ、\(\sum{y_{i}-\overline{y}}^2\)で表されます。
一方でRSSは残差変動と呼ばれ、\(\sum{y_{i}-\hat{y}_{i}}^2\)で表されます。
どちらも決定係数の計算で出てきました。
kは説明変数の数です。
F値が大きければ、「少なくとも一つの説明変数が目的変数と関係がある」と言うことがわかります。
次元が大きければ大きいほど、ペナルティがかかり、F値が大きくならない仕組みになっていますね。
この意味で、Lasso回帰や背景知識に基づく変数選択は非常に重要です。
経験的には、\(説明変数の数< \sqrt{sample size}\)だと漸近正規性の観点では問題はないとされます。
平均効果モデル：関心のあるパラメータが一つある
予測モデル：パラメータに関心がない。予測の精度に関心がある。
リサーチクエスチョンを設定する際には、以上のうちどれに当たるのかを意識しておきましょう。
ボンフェローニ補正(Bonferroni Compensation)
検定の多重性を避ける方法のうち、有力なものの一つは「ボンフェローニ補正」といいます。
実際に行うはずだった有意水準を、行うt検定の回数で割った数を、実際の有意水準とする補正方法です。
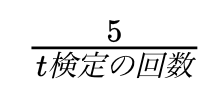
問題では、4つの水準(色)のうち2つの組み合わせを全てt検定していくものでした。よって6通りですね。
ボンフェローニ補正による有意水準は5/6で0.83%となります。
6回連続で行った場合でも、\(6×0.83=5%\)有意水準でt検定を行えたことになります。
みてわかる通り、かなり厳しい有意水準になっています。
ボンフェローニ補正による有意水準によって、有意差が出る場合はかなり少なく、あまり使われていません。
ただ、補正の中で一番理解されやすいので、統計検定では頻出です。
統計検定のチートシートは以下をクリック！
【最短合格】統計検定準一級のチートシート|難易度や出題範囲について
【最短】統計検定2級合格ロードマップとチートシート|おすすめの本について
【非等分散編】pythonでWelchのt検定をやってみた では、実際にボンフェローニ補正を使っています。
有意水準とp値について復習したい方はこちらをご覧ください。
【仮説検定】p値をゼロから解説(第一種の過誤,第二種の過誤,検出力)
