【統計検定2級】分散分析の信頼区間について|python
統計検定2級の中でも手強い分野の一つ、「分散分析」を扱います。
中でも、分散分析の信頼区間は盲点になることが多いです。例題を通して学んでいきましょう。
分散分析について基礎から学びたい方は、以下のコンテンツをご覧ください。
【統計検定2級で最も手強い(主観)】分散分析について解説します①
【統計検定2級で最も厄介(主観)】分散分析を解説します②
分散分析の信頼区間
分散分析は、複数の群内の平均値の比較を行うことで、群間または群内の平均値の差が統計的に有意かどうかを検定する統計的手法です。
信頼区間は、平均値の一定の範囲を示し、その信頼区間内に実際の平均値が含まれる確率が一定であることを表します。
分散分析の信頼区間を求めるには、以下の手順を踏むことができます:
対象とする群間の平均値の差に対応する統計量(例えば、F統計量)を求めます。
その統計量に対応する分布(例えば、F分布)から、信頼水準に応じた確率外側にある点を求めます。
1.で求めた統計量と、2. で求めた確率外側にある点から、信頼区間を求めます。
以下は分散分析の信頼区間です。
$$\overline{x} – t_{\frac{\alpha}{2} \cdot df_{E}} \cdot \sqrt{\frac{V}{n_{i}}} \leq \mu \leq \overline{x} + t_{\frac{\alpha}{2} \cdot df_{E}} \cdot \sqrt{\frac{V}{n_{i}}}$$
\(df_{E}\):残差の自由度
\(V_{E}\):残差平均平方
\(n_{i}\):i番目のサンプルサイズ
かなりややこしいです。
特に、残差の平均平方がわかっていないと信頼区間が求められないのが厄介です。
例題
あるウェブサイトの管理人は、サイトの読み込み速度(Total Blocking Time)が1000ミリ秒と、かなり遅くなっていることに気づき、直そうとしました。
考えついた対策は、以下の3つです。
対策1:アップロードした画像を最適なフォーマットに自動変換するプラグインを入れる
対策2:オフスクリーン画像の遅延読み込みを行う
対策3:使用されていないJavascriptを減らす
それぞれの対策の効果を測定するために、一元配置分散分析を行うことにしました。
以下は、それぞれの対策を水準にとり、繰り返し4回の合計12回の時間計測実験を行った時の実験結果表です。
単位はミリ秒としています。
| 対策 | 実験1回目 | 実験2回目 | 実験3回目 | 実験4回目 |
| 1(プラグイン) | 620.1 | 656.2 | 720.9 | 660.1 |
| 2(オフスクリーン) | 490.1 | 582.1 | 590.6 | 428.8 |
| 3(Js) | 281.0 | 300.7 | 190.9 | 187.2 |
この実験結果に基づいて、分散分析表を作ることにしました。
| 要因 | 平方和 | 自由度 | 平均平方 | F値 |
| 対策 | 373541.1 | ? | ? | ? |
| 誤差 | 33201.45 | ? | ? | – |
| 総計 | 406742.5 | ? | ? | – |
ただし,\(y_{j,i}\) を対策 j の第 i 回目の実験結果としたとき,データの構造を表すモデルとして、以下を想定します。
$$y_{j,i}=μ+α_{j}+ε_{j,i}$$
ここで,μ は一般平均,\(α_j\) は対策 j の効果,\(ε_{j,i}\) は互いに独立に正規分布\(N(0,σ^2)\)に従う誤差項とします。
(1)各要因の自由度を定め,F分布の自由度を求めてみましょう。
(2)実験結果からも明らかなように、管理人は対策3(js)を取ることにしました。
対策3の効果の点推定値は、-760.05(ミリ秒)です。
この効果の95%信頼区間を求めてみましょう。
 | 統計学基礎改訂版 日本統計学会公式認定統計検定2級対応 [ 日本統計学会 ] 価格:2,420円 |
解説
(1)各対策の自由度を求める問題でした。【統計検定2級で最も手強い(主観)】分散分析について解説します①の復習ですが、
水準間の自由度は、水準のサンプル数から1を引いたもの。今回の水準は対策のことなので、3(対策の種類)-1で2です。
全体の自由度は、行数×列数-1です。3種類の対策×4回の実験なので12です。12-1で自由度11です。
残差の自由度は、全体の自由度から水準間の自由度を除いたものです。11-2で9になります。
F分布の自由度は、対策の自由度と残差の自由度になります。よってF(2,9)です。
| 要因 | 平方和 | 自由度 | 平均平方 | F値 |
| 対策 | 373541.1 | 2 | ? | ? |
| 誤差 | 33201.45 | 9 | ? | – |
| 総計 | 406742.5 | 11 | ? | – |
このように分散分析表を埋めることができたと思います。
(2)分散分析の信頼区間を求める問題でした。
再喝しておきます。
$$\overline{x} – t_{\frac{\alpha}{2} \cdot df_{E}} \cdot \sqrt{\frac{V}{n_{i}}} \leq \mu \leq \overline{x} + t_{\frac{\alpha}{2} \cdot df_{E}} \cdot \sqrt{\frac{V}{n_{i}}}$$
\(df_{E}\):残差の自由度
\(V_{E}\):残差平均平方
\(n_{i}\):i番目のサンプルサイズ
今回点推定値が、-760.05(ミリ秒)と示されています。これを標本平均として扱います。
残差の平均平方は、残差平方和を残差の自由度で割れば良いので、
33201.5 ÷ 9 = 3689.06です。 i番目のサンプルサイズは、実験回数と考えて4回です。
また、95%信頼区間なのでt分布表(自由度9)を見て、\(t_{\frac{α}{2}}(9)\) =2.26 です。
\(df_E = 9\)
\(V_E = 3689.06\)
\(n_i = 4\)
\(t_{\frac{α}{2}(9)} = 2.26\)
$$-760.05-2.26×\sqrt{\frac{3689.06}{4}}≦μ≦-760.05+2.26×\sqrt{\frac{3689.06}{4}}$$
結果は、以下のようになります。手頃なところで四捨五入してください。
$$-828.6835≦μ≦-691.4165$$
つまり、対策3を100回実行すると、95回はこちらの信頼区間の間に入る「ミリ秒」だけロード時間を短縮できそうだ、ということが言えます。
CODE|python
ここでは、分散分析の信頼区間をpythonを使って算出+分布を可視化するコードを紹介いたします。
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
# 群数とデータ数
num_groups = 3
num_data = 100
# 各群からランダムなデータを生成
group1 = np.random.normal(100, 10, num_data)
group2 = np.random.normal(90, 10, num_data)
group3 = np.random.normal(110, 10, num_data)
# 各群を結合
data = np.concatenate([group1, group2, group3])
# 各群のグループ番号を作成
group_labels = np.concatenate([np.zeros(num_data, dtype=int), np.ones(num_data, dtype=int), 2*np.ones(num_data, dtype=int)])
# 分散分析を実行
f_val, p_val = stats.f_oneway(group1, group2, group3)
# 信頼区間を計算
mean_diff = np.abs(np.mean(group1) - np.mean(group2))
t_critical = stats.t.ppf(0.975, 2 * num_data - 2)
mean_diff_std_err = np.sqrt((np.var(group1) / num_data) + (np.var(group2) / num_data))
mean_diff_conf_int = mean_diff - t_critical * mean_diff_std_err, mean_diff + t_critical * mean_diff_std_err
# 結果を表示
print("F-value: ", f_val)
print("P-value: ", p_val)
print("Confidence Interval for Mean Difference: ", mean_diff_conf_int)
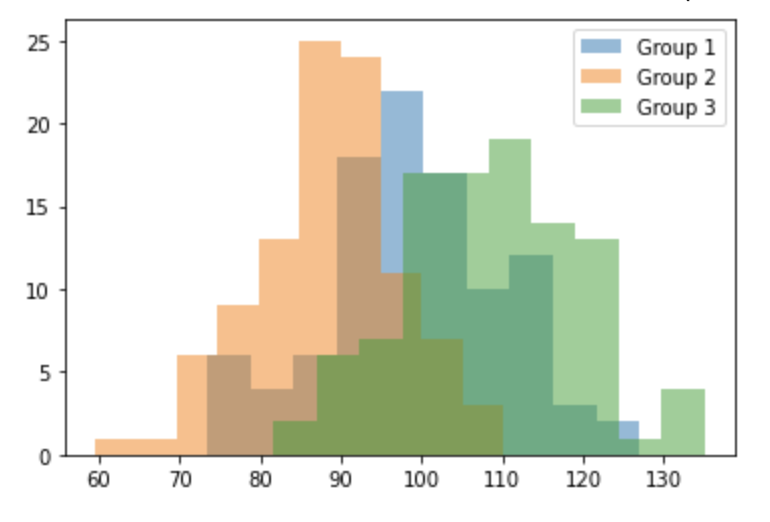
# ヒストグラム
plt.hist(group1, alpha=0.5, label='Group 1')
plt.hist(group2, alpha=0.5, label='Group 2')
plt.hist(group3, alpha=0.5, label='Group 3')
plt.legend()
plt.show()F-value: 92.87174529237846 P-value: 4.7037410752812555e-32 Confidence Interval for Mean Difference: (7.8745099949211586, 13.55453053698663)
以下手順です。
1:必要なライブラリのインポート:NumPy、SciPy、Matplotlibの3つのライブラリをインポートします。
2:群数とデータ数の定義:今回は3つの群を生成し、各群に50個のデータを含めるように定義します。
3:ランダムなデータの生成:各群から平均値が100、90、110で分散が10の正規分布からランダムなデータを生成します。
4:群の結合:各群を結合して1つのデータセットを作成します。
5:グループ番号の生成:各群に対応するグループ番号を生成します。
6:分散分析の実行:SciPyのf_oneway関数を使用して分散分析を実行します。この関数は、F値とP値を返します。
7:信頼区間の計算:2つの群間の平均値の差の信頼区間を計算します。この計算には、t分布を使用します。
8:結果の表示:分散分析の結果(F値、P値、信頼区間)を表示します。
9:ヒストグラムの作成:各群から生成されたデータの分布を視覚化するためにヒストグラムを作成します。
これにより、ランダムなデータから分散分析の信頼区間を求めることができます。
もっと力をつけたい方へ(電卓必須)|R
| 要因 | 平方和 | 自由度 | 平均平方 | F値 |
| 対策 | ? | 2 | ? | ? |
| 誤差 | ? | 9 | ? | – |
| 総計 | ? | 11 | ? | – |
水準間平方和と残差平方和を求めてみてください。参考は、【統計検定2級で最も厄介(主観)】分散分析を解説します②をご覧ください。
とても大変です。以下解説です。
①水準間平方和を求める。
まず各対策を行ったことによるミリ秒の平均を取ります。
a<-(620.1+656.2+720.9+660.1+490.1+582.1+590.6+428.8+281.0+300.7+190.9+187.2)
b<-x/12
b結果は、475.725でした。では、次にそれぞれの対策の平均と475.725の差の平方を取りましょう。
x2<-188.6^2 * 4
x2
#対策1
y2<-47.175^2 *4
y2
#対策2
z2<-235.775^2 *4
z2
#対策3x2、y2、z2はそれぞれ、142279.8、8901.922、222359.4でした。和を取りましょう。
よって水準間平方和は、373541.1となります。
②残差平方和を求める。
x3<-(664.325-620.1)^2 + (656.2-664.325)^2 +(720.9 - 664.325)^2 + (664.325 - 660.1)^2
x3
y3<-(552.9-490.1)^2 + (582.1-552.9)^2 +(552.9 - 428.8)^2 + (590.6 - 552.9)^2
y3
z3<-(239.95-190.9)^2 + (281.0-239.95)^2 +(239.95 - 300.7)^2 + (239.95 - 187.2)^2
z3
w3<-5222.597 + 20197.29 + 7781.567
w3それぞれの対策の平均を求めた後、偏差の平方和をとり、最終的に1,2,3で和をとったものが残差平方和になります。
答えは、33201.45になります。
これらの計算をRで簡単に行うコンテンツはこちらから。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


