【統計検定】ポアソン過程をわかりやすく解説|待ち行列理論
こんにちは、青の統計学です。
今回は統計検定準一級から登場する確立過程の一つ「ポアソン過程」について解説いたします。
このコンテンツに全て詰まっているのでブックマーク推奨です!
関わりの深い生存時間解析は、こちらで学習できます。
ポアソン過程とは(poisson process)
ポアソン過程は、連続的な時間確率過程のうち自然数しかとらないという特徴を持ちます。
つまり、現実世界における何らかの回数や発生頻度などをモデル化するために使用されます。
地震や交通事故、火事の回数や熱力学の断熱変化、損保数理でも登場します。
基本情報/応用情報技術者試験でもよく出る待ち行列理論やネットワークトラフィックのモデリングにも使われていますね。
まず、\(N_t\)を時間tまでに発生した事象の数を表します。
\(N_t\)は強度(後述します)\(\lambda_t\)のポアソン分布に従います。
$$P(N_t=k)=e^{-\lambda_t}\frac{(λt)^k}{k!}$$
特徴1:独立増分過程
先述した通り、ポアソン過程は
観測を始めてから、事象が発生した回数を\(t_1,t_2,…\)と表していきます。
$$0<t_1<t_2<…<t_k$$
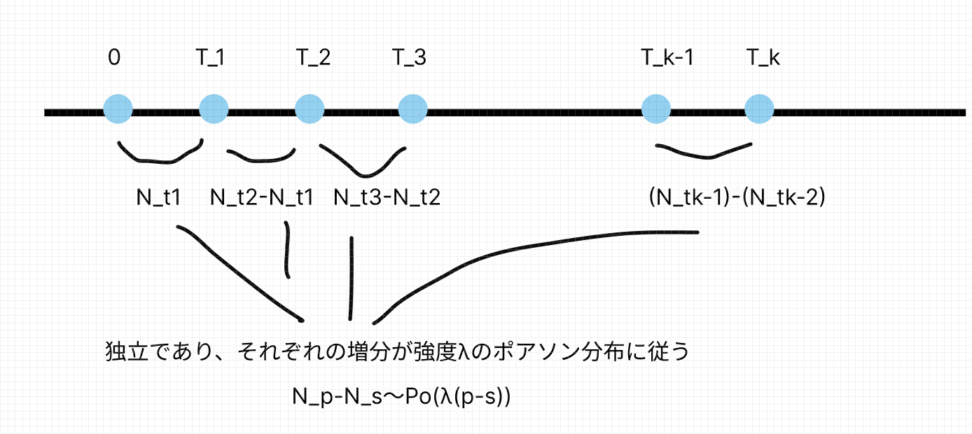
図で言うと\(\lambda\)は強度(intensity)を表し、強度が上がると事象の発生頻度が上がっていく仕組みです。
そして、時間差(増分)は独立で同一な分布に従います(i.i.d)。
$$P(N(t+s) – N(t) = n | N(t) = m) = P(N(s) = n)$$
この独立性についてわかりやすく言えば以下のようになります。
例えば、公園で鳥が鳴くことを考えてみましょう。 鳥が鳴くのはランダムなタイミングで、一日中いつでも起こり得ます。この「鳥が鳴く」という事象がどのように時間とともに起こるかを表すのがポアソン過程です。 →独立性というのは、一つの事象が起こることが他の事象に影響を与えないということです。 つまり、一羽の鳥が鳴いたからといって、次に鳥が鳴くのが早まったり遅くなったりすることはありません。
このようにある事象がどのようにランダムに起きるかをモデル化できるので応用範囲は広いということです。
また、どの時間帯でも確率は変わらないという一様性も特徴の一つです。
特徴2:強度λ(平均到着率)
ある時間間隔における事象の平均数は、その間隔の長さに比例します。
これは以下のように表されます
$$E[N(t)] = \lambda_t$$
ここで、\(E[N(t)]\)は時間tまでに発生した事象の数の期待値(平均)を表し、\(\lambda\)は強度(事象が発生する平均的な速度)を表します。
補論|ポアソン過程はマルチンゲールなのか?
確率過程には、マルチンゲールという特徴を持つものがあります。
$$E[Y_{n}|Y_{n-1},..,Y_{0}]=Y_{n-1}$$
上のように、時点\(n-1\)における時点\(n\)の\(Y\)の条件付き期待値(上の式)は、時点\(n-1\)のYと同様に確からしいということです。つまり将来の値が現在の情報に基づいて予測される確率過程の一種で、その期待値が現在の値と常に等しいという特性を持ちます。
ランダムウォークなどの確率過程はマルチンゲールです。
以下のコンテンツでマルチンゲールについては解説しています。
どの時点においても条件付き期待値が同じということは、強度(平均到着率)が時間に依存しなければポアソン過程はマルチンゲールであると言えますね。
つまり、事象が発生する平均的な速度が時間とともに変化するポアソン過程は、一般的にはマルチンゲールではありません。
ポアソン分布との違い(poisson distribution)
t時点の確立過程\(N_t\)が強度\(\lambda_t\)のポアソン分布に従うことから、ポアソン過程を理解するには、ポアソン分布の理解が必要です。
詳しくはこちらのコンテンツをご覧いただきたいですが、少しこちらでも解説いたします。
$$p(x)=\frac{\lambda^x}{x!}e^{-\lambda}$$
ポアソン分布は、一定の時間または空間内で平均的にλ回(生起率)起こる事象が、その時間または空間内でk回起こる確率を表す確率分布です。
つまり、ポアソン分布は「一定の時間または空間内で事象が何回起こるか」に焦点を当てています。
嬉しいことに、期待値も分散も\(\lambda\)(生起率)です。
ポアソン過程は、一定の強度でランダムに発生する事象をモデル化する確率過程です。
つまり、ポアソン過程は「事象がどのように時間とともに発生するか」に焦点を当てています
ちなみにポアソン過程では、時間tまでに発生する事象の数の期待値は\(\lambda_t\)であり、その分散も\(\lambda_t\)です。
ポアソン過程の応用例|待ち行列理論
ポアソン過程は待ち行列理論における到着とサービスのモデリングに広く用いられます。
待ち行列理論は、システムが要求をどのように処理するかを研究する分野です。
これには、要求がシステムに到着する頻度(到着率)と、システムが要求を処理する速度(サービス率)が含まれます。
一般的なM/M/1待ち行列モデルを考えてみましょう。
このモデルでは、到着がポアソン過程に従い(平均到着率\(\lambda\))、サービス時間が指数分布に従う(平均サービス率\(\mu\))と仮定します。
このとき、システムの状態(システム内の要求の数)は、時間とともにマルコフ過程を形成します。
システムの状態遷移率は以下のようになります。
$$q_{ij} =\begin{cases}\lambda & \text{if } j = i + 1 \\mu & \text{if } j = i – 1 \\0 & \text{otherwise}\end{cases}$$
指数分布について
脱線しますが、指数分布は以下のような形で表される連続型の確率分布で、機械の耐用年数や地震の発生間隔の事前分布として使われます。
パラメータ\(\theta\)が大きくなればなるほど、減衰速度が下がっていくイメージです。
$$Exponetial(x|\theta)=\frac{x}{\theta}exp(-\frac{x}{\theta})$$
期待値はパラメータ\(\theta\)で、分散は\(\theta^2\)です。
統計検定準一級を受けるなら証明できるようになりましょう。
情報処理技術者試験についてのチートシートはこちら。
【試験直前ッ】基本情報・応用情報の午前チートシート|セキュリティ編
【試験直前ッ】基本情報・応用情報の午前チートシート|ネットワーク編
【試験直前ッ】基本情報・応用情報の午前チートシート|データベース&プログラミング編
【試験直前ッ】基本情報・応用情報の午前チートシート|システム編
【試験直前ッ】基本情報・応用情報の午前チートシート|開発・マネジメント編
【試験直前ッ】基本情報・応用情報の午前チートシート|テクノロジー編
【忙しい人のための】基本情報・応用情報の午前チートシート|総集編
CODE|ウェブサイトへの訪問頻度を考える
今回はウェブサイトの訪問がどう発生するのかをモデル化しようと思います。
何となく想像がつくと思いますが、ウェブサイトの訪問確率は一様ではありません。つまり、強度(平均到着率)が時間依存的という意味でマルチンゲールではないポアソン過程を考えています。
ちなみに、青の統計学では平日昼の訪問が極めて多いです。
お仕事や勉強で使われているのでしょうか。
import numpy as np
import matplotlib.pyplot as plt
# シミュレーション時間(時間)
T = 24
# 時間帯ごとの平均到着率(強度)(1時間あたりの平均訪問数)
lambda_rate = [2]*8 + [10]*12 + [2]*4
# ポアソン過程をシミュレート
arrival_times = []
for t in range(T):
n_arrivals = np.random.poisson(lambda_rate[t])
arrival_times.extend(t + np.random.uniform(0, 1, n_arrivals))
# ポアソン過程をプロット
plt.figure(figsize=(10, 6))
plt.hist(arrival_times, bins=24, edgecolor='black')
plt.xlabel('Time (hours)')
plt.ylabel('Number of visits')
plt.title('Website visits over 24 hours')
plt.grid(True)
plt.show()
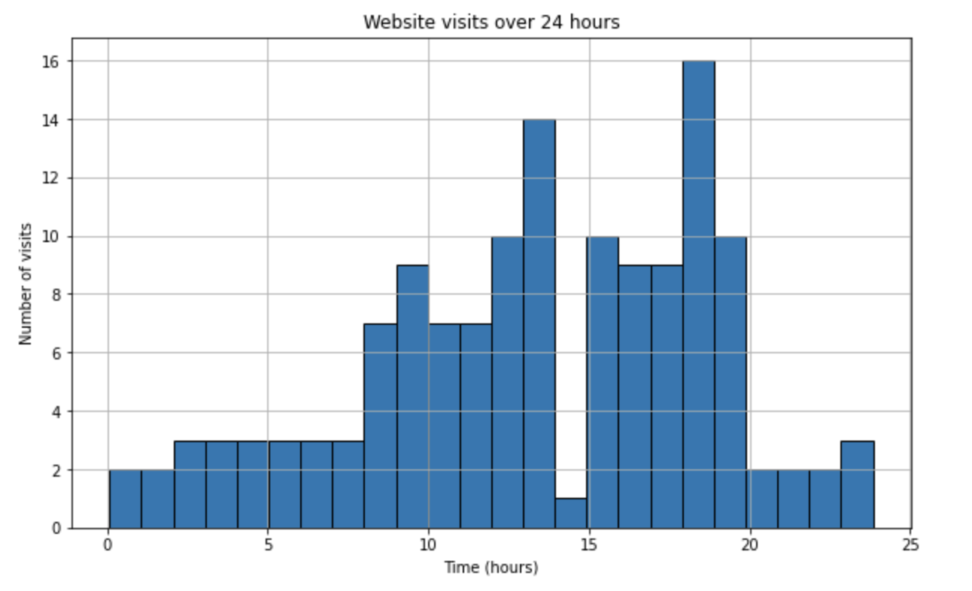
lambda_rate = [2]*8 + [10]*12 + [2]*4
ここで、[2]*8は、0時から7時までの8時間の間に平均的に2回の訪問があることを意味します。つまり、この時間帯の平均到着率は2です。
次に、[10]*12は、8時から19時までの12時間の間に平均的に10回の訪問があることを意味します。つまり、この時間帯の平均到着率は10です。
最後に、[2]*4は、20時から23時までの4時間の間に平均的に2回の訪問があることを意味します。つまり、この時間帯の平均到着率は2です。
したがって、lambda_rateは一日24時間の各時間帯における平均到着率を表すリストとなります。
このリストは、非定常ポアソン過程のシミュレーションに使用され、ウェブサイトへの訪問が昼間の時間帯に集中するという現実のパターンを反映しています。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


