Python

HOME
Python
【分類タスク】ロジスティック回帰の使い方|python

11/27/2022 / 最終更新日時 : 09/09/2024 bluest Python

【分類タスク】ロジスティック回帰の使い方|python

重回帰モデルは、1つの目的変数に対して、説明変数が複数あるモデルです。

今回ご紹介する、「ロジスティック回帰」は目的変数が数値型ではなく、「Yes or No」の2値であるということが最大の特徴です。

pythonではなく、Rで見たい方は【二項分布】ロジスティック回帰について(実例つき)をご覧ください。

回帰分析については、こちらをどうぞ。

ロジスティック回帰(logistic regression)

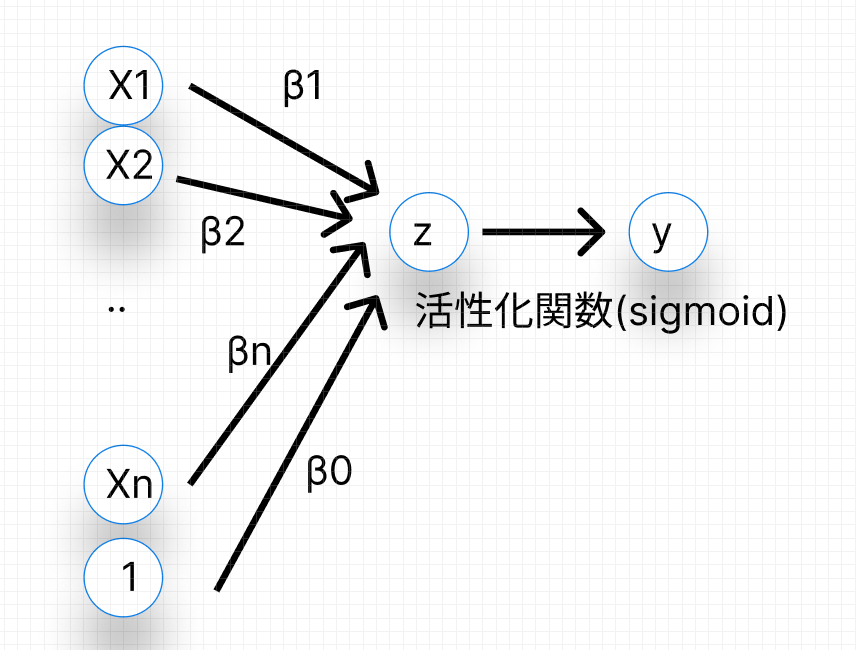
前述の通り、ロジスティック回帰は重回帰モデルの派生です。

上のモデルで言うと、zだと重回帰モデルです。しかし、zに活性化関数を導入してあげると出力をリッチにすることができます。

今回のロジスティックモデルでは、活性化関数に「シグモイド関数(後述します)」を採用しています。

活性化関数は、ReLu(ランプ関数)やソフトプラスなどがあります。

【python】活性化関数の完全ガイド|特徴と効果的な選び方について|勾配消失問題

では、具体的な原理を説明していきます。コードのみ知りたい方は、飛ばして構いません。

①確率分布：二項分布

②リンク関数：ロジットリンク関数

このようになります。注意として、カウントデータが１個のみなら①の確率分布はベルヌーイ分布になります。

二項分布(binomial distribution)

二項分布とは、独立なベルヌーイ分布をn回繰り返した時の和の分布です。

実現値が有限である点において、ポアソン分布と異なります。

【例】コインを5回投げて表の出た回数をXとすると、実現値は0,1,2,3,4,5の6種類です。表が出る確率を仮にpとすると、実現値は以下のようになります。

$$(1-p)^5$$

$$5p(1-p)^4$$

このようになっていきます。実現値0から5までの確率の和は以下のようになります。

$$p(x)={}_5C_xp^5(1-p)^{5-x}$$

一般化すると、二項分布の確率密度関数は以下のようになります。

nは実現値です。

$$p(x)={}_nC_xp^n(1-p)^{n-x}$$

ロジットリンク関数(logit link function)

先ほどの二項分布と同じコインの例を挙げます。

z<-seq(-6,6,0.1)
#線形予測子/右辺

logit<-function(z) z
#ロジット関数の定義
#リンク関数/左辺

plot(z,logit(z))
#作図

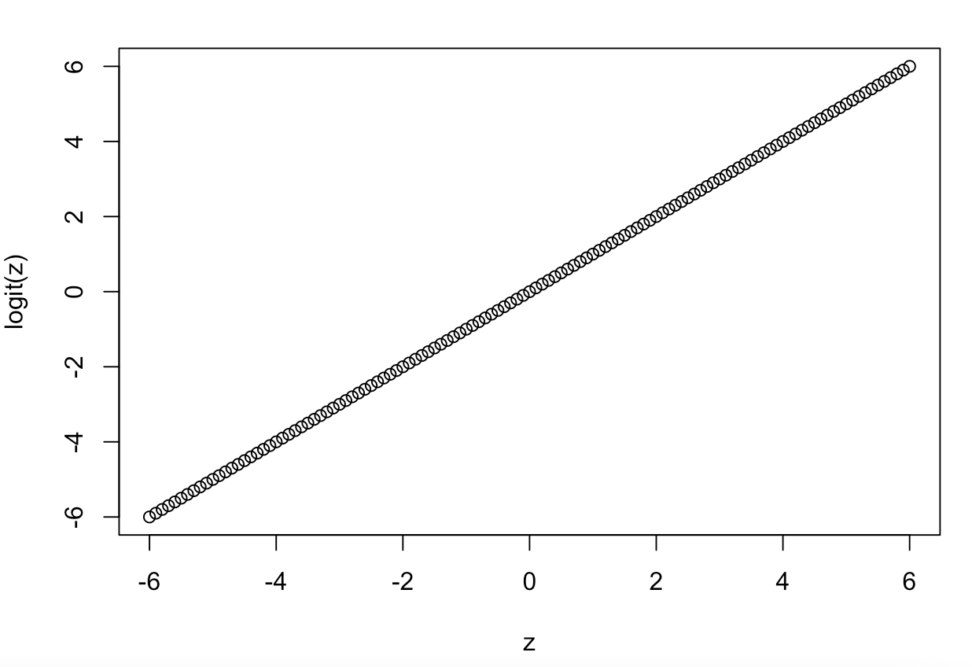
seq(a,b,c)というのは、最小値aで最大値bまでをc刻みで代入するものです。

$$log \frac{q_{i}}{1-q_{i}}=z_{i}$$

上の式がロジット関数です。右辺は線形予測子、左辺はオッズを対数化したものです。コインの例で言うと、下のようになります。

$$log \frac{コインがi回表の確率}{コインがn-i回裏の確率}=z_{i}$$

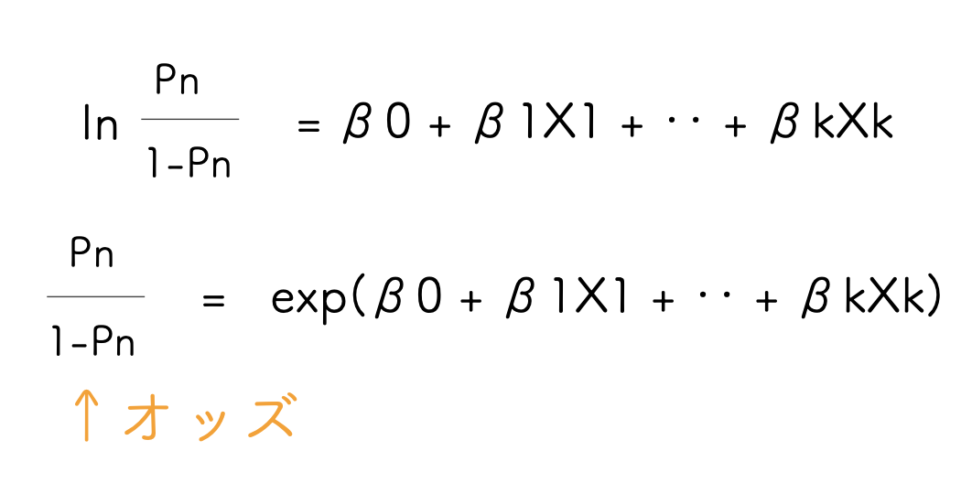
対数オッズと、オッズの関係はこのようになります。

上側の右辺がよくみる線形予測子の形です。

しかし、出力結果が、「オッズを対数化したもの」だと目的に沿わない場合もあります。

ちゃんと、「コインがi回表になる確率を知りたい！」と言う場合には、ロジット関数をロジスティック関数にする必要があります。

ロジスティック関数(logistic function)

ロジット関数の逆関数が、ロジスティック関数です。

ロジスティック関数は以下のような形になります。

$$logistic(z_{I})=\frac{1}{1+exp(-z_{i})}$$

線形予測子$z_i$に−１がかかりました。

eの-線形予測子乗に1を足したものが分母となっています。

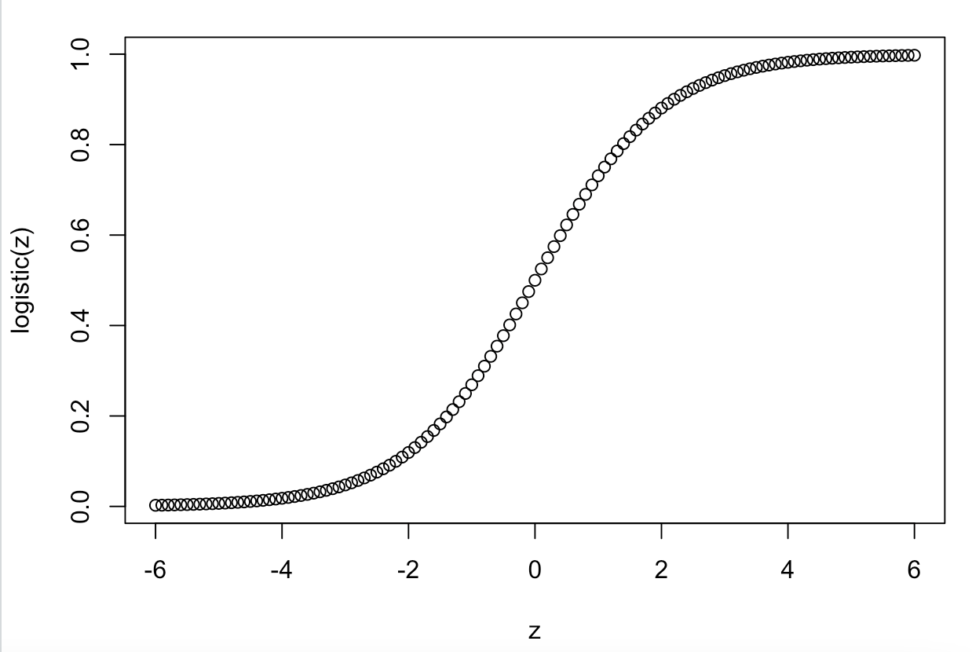
ロジット関数と比べて、滑らかになりました。

「コインが表になる確率」が上のように推移することがわかりました。

オッズ比に関して詳しく知りたい方

【ベイズ因子】オッズ比の使われ方を紹介します

補足：ロジスティック回帰のコスト関数を最尤推定量から解釈する

シグモイド関数は以下のような形で表され、0から1の値を取り、「ラベルが1になる確率を返す」ことが特徴でした。

$$h(x)=g(θ^Tx)=\frac{1}{1+e^{-z}}$$

パラメータが$θ$の時に、入力xの出力が1である確率は$P(y=1|x;θ)=h(x)$と表されます。

一方で、パラメータが$θ$の時に、入力xの出力が0である確率は$P(y=0|x:θ)=1-h(x)$と表すことができます。

これによりシグモイド関数の確率分布は以下のように表すことができます。

$$p(y|x;θ)=(h(x))^{y}(1-h(x))^{1-y}$$

では、最尤推定によりパラメータを推定します。

尤度関数は以下のような形になります。

$$L(θ)=\Pi_{i=1}^{m}(h(x)^{(i)})^{y^{(i)}}(1-h(x^{(i)}))^{1-y^{i}}$$

このまま総積の形だと計算がしづらいので対数を取ります。

$$\sum_{i=1}^{m}(logy^{I}h(x^{(i)}))+(1-y^{(i)})log(1-h(x^{i}))$$

実は上の対数尤度関数が、ロジスティック回帰の損失関数になっています。

交差エントロピー誤差関数（cross-entropy error function）と言い、正解カテゴリを予測できる確率が高くなるほど値が小さくなります。

ロジスティック回帰では、この損失関数を最急勾配降下法によって小さくしていき、最適なパラメータを探索していくアルゴリズムだということがわかります。

ちなみに線形回帰のコスト関数とは異なり、各特徴量ベクトルが独立だとしても解析的にパラメータの推定量を求めることはできず、探索的な降下法を使う必要があります。もちろん形によっては局所解に陥る可能性もありますが、確率的降下法などを使えば、一定抜け出せる可能性もあります。

また、線形やロジスティック回帰に限らず、入力データを標準化することで降下法による収束が早くなるというメリットがあるので是非行いましょう。

多値分類に使うソフトマックス関数は以下のコンテンツからご覧ください。

【Transformer】ソフトマックス関数についてわかりやすく解説｜python

CODE|python

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
import numpy as np
import pandas as pd
data_breast_cancer = load_breast_cancer()
# Pandasによるデータの表示
df_target = pd.DataFrame(data_breast_cancer["target"], columns=["target"])
df_data = pd.DataFrame(data_breast_cancer["data"], columns=data_breast_cancer["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
df.head()

では、コードの紹介です。

まず、必要なライブラリをインポートした後、データをロードします。

今回使うデータは、乳がんのデータです。

乳房塊の微細針吸引物（FNA）のデジタル化画像から計算されており、画像中に存在する細胞核の特徴を捉えたものです。

データセットの中では悪性(malignant)は0、良性(benign)は1で表されており、targetカラムで表されております。

	target	mean radius	mean texture	mean perimeter	mean area	mean smoothness	mean compactness	mean concavity	mean concave points	mean symmetry	…	worst radius	worst texture	worst perimeter	worst area	worst smoothness	worst compactness	worst concavity	worst concave points	worst symmetry	worst fractal dimension
0	0	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.3001	0.14710	0.2419	…	25.38	17.33	184.60	2019.0	0.1622	0.6656	0.7119	0.2654	0.4601	0.11890
1	0	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.0869	0.07017	0.1812	…	24.99	23.41	158.80	1956.0	0.1238	0.1866	0.2416	0.1860	0.2750	0.08902
2	0	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.1974	0.12790	0.2069	…	23.57	25.53	152.50	1709.0	0.1444	0.4245	0.4504	0.2430	0.3613	0.08758
3	0	11.42	20.38	77.58	386.1	0.14250	0.28390	0.2414	0.10520	0.2597	…	14.91	26.50	98.87	567.7	0.2098	0.8663	0.6869	0.2575	0.6638	0.17300
4	0	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.1980	0.10430	0.1809	…	22.54	16.67	152.20	1575.0	0.1374	0.2050	0.4000	0.1625	0.2364	0.07678

df.head()で表示したデータは以上です。1つの目的変数(target)に対して、30個の説明変数があります。

今回、目的変数が0or1の2値になっているのでロジスティック回帰にはぴったりですね。

y = df["target"]
X = df.loc[:, "mean radius":]
# 訓練データとテストデータに分ける
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)

yにtargetカラムを入れ、Xにmean radius以降のカラムを格納します。

その後、train_test_splitメソッドを使って学習データとテストデータに分けます。

# ロジスティック回帰クラスの初期化と学習
model = LogisticRegression()
model.fit(X_train, y_train)

print('正解率(train):{:.3f}'.format(model.score(X_train, y_train)))
print('正解率(test):{:.3f}'.format(model.score(X_test, y_test)))

→正解率(train):0.968
→正解率(test):0.954

ではモデルに入れていきます。

インスタンスを作成→fitというお決まりの機械学習の手順です。

学習データの正解率とテストデータの正解率を見比べてみましたが、大差はなく、致命的な過学習は起きていないと言えます。

最後に、係数とオッズ比を計算してみます。

オッズ比が高いほど、該当の説明変数が1単位増加した時に正解率に影響があります。

model.coef_

→array([[ 1.41677628,  0.08126053,  0.14668262,  0.00202867, -0.04785284,
        -0.24908786, -0.36871506, -0.16734009, -0.13170346, -0.01027023,
         0.05479049,  0.33605348,  0.24950049, -0.07955968, -0.00411873,
        -0.04492612, -0.07642801, -0.02530927, -0.03060011, -0.00324966,
         1.5047747 , -0.23046967, -0.29736352, -0.02614451, -0.08229005,
        -0.69886355, -0.9959647 , -0.33568285, -0.3133805 , -0.06684691]])

np.exp(model.coef_)

→array([[4.12380498, 1.08465345, 1.15798639, 1.00203073, 0.95327406,
        0.77951149, 0.69162245, 0.84591188, 0.8766009 , 0.98978233,
        1.05631929, 1.39941387, 1.2833842 , 0.9235229 , 0.99588974,
        0.95606812, 0.92641961, 0.97500833, 0.96986334, 0.99675561,
        4.50313894, 0.79416052, 0.74277395, 0.97419429, 0.92100479,
        0.49714997, 0.36936694, 0.71484978, 0.73097172, 0.93533838]])

4.12と4.50という大きめのオッズ比が目につきます。

どんなカラムなのでしょうか。