ガウス過程回帰の仕組みと実務での応用をわかりやすく解説|ノンパラメトリック機械学習
こんにちは、青の統計学です。
今回はガウス過程回帰について解説いたします。

製造業の現場など、n=20やそこらぐらいのデータセットで予測を行う必要がある時にもよく使われます。ガウス過程は少数データとの相性がよく、予測値の分散まで出せるのがメリットです。
従来の多くの回帰手法は、一つの「点」としての予測値(平均値)を出すことに主眼を置いています。しかし、ビジネス上でリスクを推し量る時に、その予測が持つ不確かさ、つまり予測のブレ幅が問われることが結構あります。
この不確かさを定量的に、今回解説するガウス過程回帰(Gaussian Process Regression, GPR)です。
早速みていきましょう!
数学的背景
ガウス過程回帰を理解するためのポイントは、その名の通り「ガウス過程」にあります。
ガウス過程とは、普段が慣れ親しんでいる「ガウス分布(正規分布)」を、「関数」という無限次元の対象にまで拡張した概念です。
ガウス分布(正規分布)の復習:多次元への拡張
まずは基本の復習です。
正規分布について復習していきましょう。
もう少し丁寧に復習したい方はこちらをどうぞ
さて、1次元のガウス分布は、平均 $\mu$ と分散 $\sigma^2$ の二つのパラメータで完全に決定される、釣り鐘型の分布です。
確率密度関数は、
$$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) $$
で表されます。
これを多次元に拡張したものが多変量ガウス分布ですね。これは、複数の確率変数 $X = (X_1, X_2, \dots, X_D)^T$ が同時に従う分布で、平均ベクトル $\boldsymbol{\mu}$ と共分散行列 $\boldsymbol{\Sigma}$ の二つのパラメータで決定されます。
$$p(\boldsymbol{x}) = \frac{1}{\sqrt{(2\pi)^D |\boldsymbol{\Sigma}|}} \exp\left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\boldsymbol{x}-\boldsymbol{\mu})\right)$$
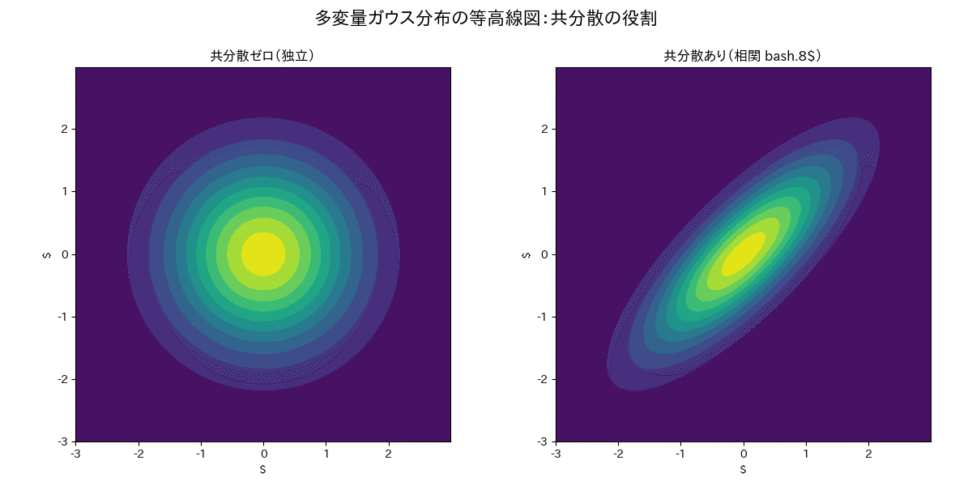
ここで重要なのは、共分散行列 $\boldsymbol{\Sigma}$ の役割です。
$\boldsymbol{\Sigma}$ の対角成分は各変数の分散(ブレ幅)を表し、非対角成分は変数間の共分散(連動性)を表します。つまり、ある変数 $X_i$ の値を知ることで、別の変数 $X_j$ の値についてどれだけ情報が得られるか、その関係性を表現しているのです。
ガウス過程の定義:関数空間のガウス分布
ガウス過程は、この多変量ガウス分布の考え方を、無限次元の確率変数、すなわち関数にまで拡張したものです。 ガウス過程とは、「任意の有限個の入力点 $x_1, x_2, \dots, x_n$ における関数の値 $f(x_1), f(x_2), \dots, f(x_n)$ が、必ず多変量ガウス分布に従う」という性質を持つ確率過程です。
$$f(x_1), f(x_2), \dots, f(x_n))^T \sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{K}$$
- $\boldsymbol{\mu}$
- 平均関数 $m(x)$ を用いて計算される平均ベクトル
- $\boldsymbol{\mu} = (m(x_1), m(x_2), \dots, m(x_n))^T$
- $\boldsymbol{K}$ は、共分散関数 $k(x_i, x_j)$ を用いて計算される共分散行列(カーネル行列)
$ \boldsymbol{K}_{ij} = k(x_i, x_j) $つまり、ガウス過程は、関数 $f(x)$ の「形」そのものに対する確率分布を定義しているのです。

関数を無限次元のベクトルと捉え、そのベクトルが従う確率分布がガウス分布である、とイメージすると、わかりやすいでしょうか。
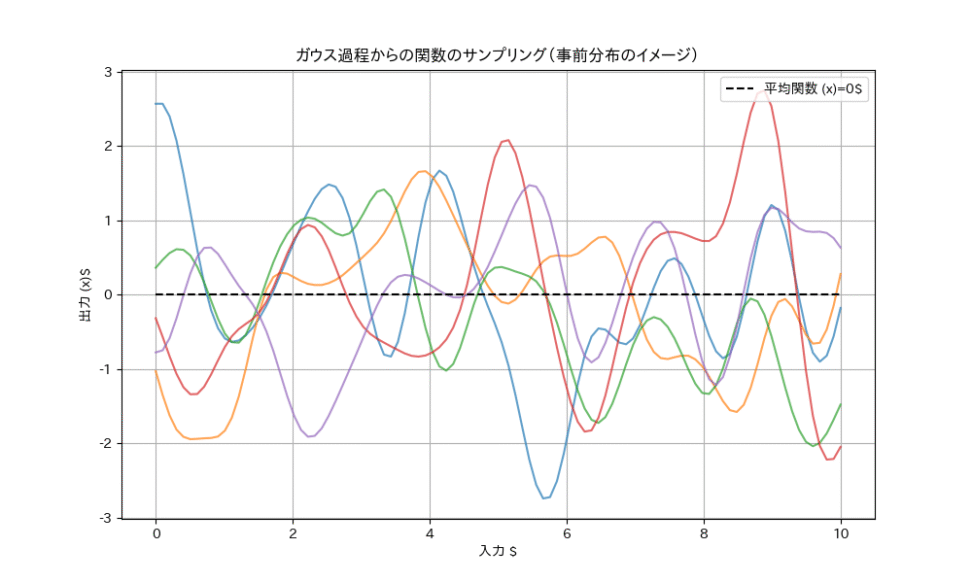
ベイズ線型回帰とは異なり、基底関数を明示的に与えなくて良いというメリットがあり、関数の分布を直接仮定するという特徴がある、というのがポイントですね。
平均関数\(m(\boldsymbol{x} )\)について
平均関数は\(m(x)\) は、ガウス過程における任意の点 \(x\)における関数の期待値を表します。
つまり、関数の出力がどの程度の値になるかの「平均的な」予測を提供します。
多くの場合、平均関数はゼロ関数(すなわち、すべての x に対して\(m(x)=0\))として設定されます。
これは、ガウス過程が主に関数の形状をモデル化するため、関数が0の周辺にあることを仮定しています。
共分散関数(カーネル関数)
ガウス過程の性質を決定づけるのが共分散関数 $k(x_i, x_j)$、通称カーネル関数です。
カーネル関数 $k(x_i, x_j)$ は、二つの入力点 $x_i$ と $x_j$ がどれだけ「似ているか(類似度)」を測る関数です。
そして、この類似度が、対応する関数の出力値 $f(x_i)$ と $f(x_j)$ の共分散(連動性)になる、という役割を果たします。
$$\text{類似度} \quad k(x_i, x_j) \quad \rightarrow \quad \text{共分散}$$
もし $x_i$ と $x_j$ が非常に近ければ、$k(x_i, x_j)$ は大きな値を取り、対応する関数の値 $f(x_i)$ と $f(x_j)$ は強く連動します。
つまり、

「入力が似ていれば、出力も似ているはずだ」という、暗黙的に仮定している滑らかさの仮定を、数学的に表現しているわけですね。
逆に、 $x_i$ と $x_j$ が遠ければ、$k(x_i, x_j)$ は小さな値を取り、関数の値はほとんど独立になります。
で、最も一般的に使われるカーネルの一つが、RBFカーネル、またはガウスカーネルです。
カーネルについては、この記事でも詳しく扱っています。
【python】カーネルSVMとは?kernel関数を利用した非線形データの判別問題に挑戦|機械学習
$$k(x_i, x_j) = \sigma_f^2 \exp\left(-\frac{|x_i – x_j|^2}{2l^2}\right)$$
- $\|x_i – x_j\|^2$ :入力点間の距離の二乗
- 距離が離れるほど、指数関数的に類似度が減少します。
- $l$ :長さスケールと呼ばれるハイパーパラメータで、関数の「滑らかさ」を制御します。
- $l$ が小さいほど関数はギザギザに、大きいほど滑らかになります。
- $\sigma_f^2$ :信号の分散
- 関数の値の全体的な振幅(スケール)を制御します。
ガウス過程回帰の仕組み:ベイズ周りの話
ガウス過程回帰は、このガウス過程を「関数に対する事前分布」として利用し、観測されたデータ(学習データ)を用いて、予測したい新しい点における関数の値の事後分布を導出する、というベイズ統計学の枠組みで動作します。
不確実性を定量化できると冒頭説明したのも、この仕組みがあるからですね。
ベイズの知識の復習はこちらがおすすめです。
事前分布と事後分布:データによる知識の更新
では、更新の手順をみていきましょう。
事前分布の設定
まず、データを見る前に、予測したい関数 $f(x)$ はガウス過程に従うと仮定します。これが事前分布です。この事前分布は、平均関数 $m(x)$ とカーネル関数 $k(x_i, x_j)$ によって完全に定義されます。
データの観測
次に、観測データ $\mathcal{D} = \{(\boldsymbol{x}_i, y_i)\}_{i=1}^n$ を得ます。ここで、観測値 $y_i$ は、真の関数値 $f(\boldsymbol{x}_i)$ にノイズ $\epsilon_i$ が加わったものと仮定します。
$$ y_i = f(\boldsymbol{x}_i) + \epsilon_i $$
ノイズ $\epsilon_i$ もまた、平均 0、分散 $\sigma_n^2$ のガウス分布に従うと仮定します。
事後分布の導出
観測データ $\mathcal{D}$ を用いて、ベイズの定理により、新しい入力点 $\boldsymbol{x}_*$ における関数の値 $f(\boldsymbol{x}_*)$ の事後分布を計算します。
小難しく言っていますが、ベイズの定理がわかっていれば、理解できる話だと思います。ベイズの定理は、概念的には以下のようになります。
$$P(\text{関数} \mid \text{データ}) \propto P(\text{データ} \mid \text{関数}) \times P(\text{関数})$$
ガウス過程の嬉しい点
事前分布と尤度(ノイズ)の両方がガウス分布であるため、事後分布もまたガウス分布になるという点がメリットとして大きいです。つまり、事後分布は、新しい入力点 $\boldsymbol{x}_*$ における予測値の平均 $\mu_*$*と分散 $\sigma_*^2$ の二つの値で完全に記述されます。
予測分布の導出:平均と分散の計算
新しい入力点 $\boldsymbol{x}_*$ における予測分布 $p(y_* \mid \boldsymbol{x}_*, \mathcal{D})$ は、多変量ガウス分布の**条件付き分布**の性質を利用して、解析的に導出できます。
観測データ $\boldsymbol{y} = (y_1, \dots, y_n)^T$ と、予測したい点 $\boldsymbol{x}_*$ における予測値 $y_*$ を合わせたベクトルは、事前分布の仮定から、以下のような多変量ガウス分布に従います。
$$\begin{pmatrix} \boldsymbol{y} \ y_* \end{pmatrix} \sim \mathcal{N} \left( \boldsymbol{0}, \begin{pmatrix} \boldsymbol{K}(\boldsymbol{X}, \boldsymbol{X}) + \sigma_n^2 \boldsymbol{I} & \boldsymbol{K}(\boldsymbol{X}, \boldsymbol{x}*) \ \boldsymbol{K}(\boldsymbol{x}, \boldsymbol{X}) & k(\boldsymbol{x}_, \boldsymbol{x}_*) + \sigma_n^2 \end{pmatrix} \right)$$
- $\boldsymbol{K}(\boldsymbol{X}, \boldsymbol{X})$ :学習データ間のカーネル行列
- $\boldsymbol{K}(\boldsymbol{X}, \boldsymbol{x}_*)$ :学習データと予測点間のカーネルベクトルです。
この同時分布から、観測データ $\boldsymbol{y}$ が与えられたときの $y_*$ の条件付き分布(事後分布)を計算すると、これもガウス分布 $\mathcal{N}(\mu_*, \sigma_*^2)$ になり(さっきの、ガウス過程の嬉しさ〜で言及したポイント)、その平均 $\mu_*$ と分散 $\sigma_*^2$ は以下の式で得られます。
予測平均(予測値)
$$\mu_* = \boldsymbol{K}(\boldsymbol{x}_*, \boldsymbol{X}) \left[ \boldsymbol{K}(\boldsymbol{X}, \boldsymbol{X}) + \sigma_n^2 \boldsymbol{I} \right]^{-1} \boldsymbol{y}$$
予測分散(いわゆる不確かさ)
$$\sigma^2_* = k(\boldsymbol{x}, \boldsymbol{x}) + \sigma_n^2 – \boldsymbol{K}(\boldsymbol{x}, \boldsymbol{X}) \left[ \boldsymbol{K}(\boldsymbol{X}, \boldsymbol{X}) + \sigma_n^2 \boldsymbol{I} \right]^{-1} \boldsymbol{K}(\boldsymbol{X}, \boldsymbol{x})$$
なんと、ガウス過程回帰は、データ間の類似度(カーネル)と、多変量ガウス分布の性質という、二つの要素だけで、予測値とその区間を同時に計算できてしまいました!
カーネル法との共通点
ここまでみてきた通り、ガウス過程回帰は、SVMや主成分分析といったカーネル法と同じく、カーネルトリックを利用しています。カーネル関数 $k(\boldsymbol{x}_i, \boldsymbol{x}_j)$ は、入力 $\boldsymbol{x}$ を、より高次元(あるいは無限次元)の特徴量ベクトル $\phi(\boldsymbol{x})$ にマッピングし、その空間での内積 $\phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}_j)$ を計算していると解釈できます。
ガウス過程回帰は、線形回帰の枠組みを、カーネル関数を使って、非線形な問題にも適用できるように拡張した、より包括的な手法だと捉えるのが立ち位置として理解しやすいと思います。
おまけ|少数データと不確実性への対応
予測の不確かさ(分散)の活用
ガウス過程回帰の最大の利点は、予測値 $\mu_*$ と同時に、その予測分散 $\sigma_*^2$を得られることです。
この幅が、実務において必要になるケースが多いです。
ちょっと図を見てみましょう。
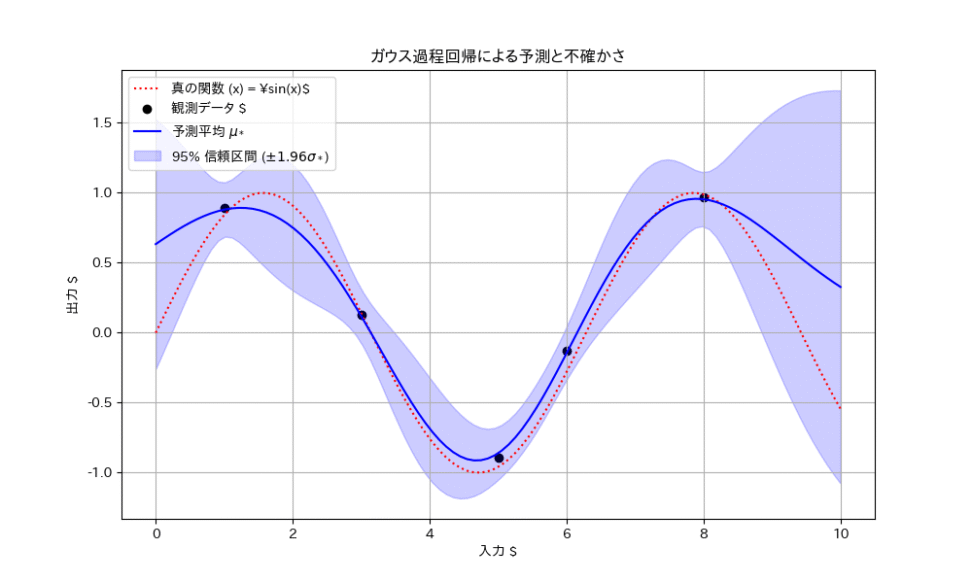
図からわかるように、予測分散 $\sigma_*^2$ は、以下の二つの要因で大きくなります。
- データから遠い領域
- 学習データが存在しない領域や、データ点から離れた領域では、モデルは自信を持って予測できないため、分散が大きくなります。
- データのノイズ観測ノイズ
- $\sigma_n^2$ が大きい場合、予測全体に対する不確かさが増し、分散が大きくななっていますね。
応用例:ベイズ最適化
予測分散の応用例の一つが、ベイズ最適化です。
これは、実験やシミュレーションのコストが高い場合に、最も効率的に最適なパラメータの組み合わせを見つけ出すための手法です。 kaggleとかをやっていると聞いたことがある方もいるのではないでしょうか。

シンプルに、いっぱい計算するのがめんどくさいので、良さそうなパラメータを順に選んで計算しているということですね。グリッドサーチやランダムサーチよりは、賢いやり方ですね。
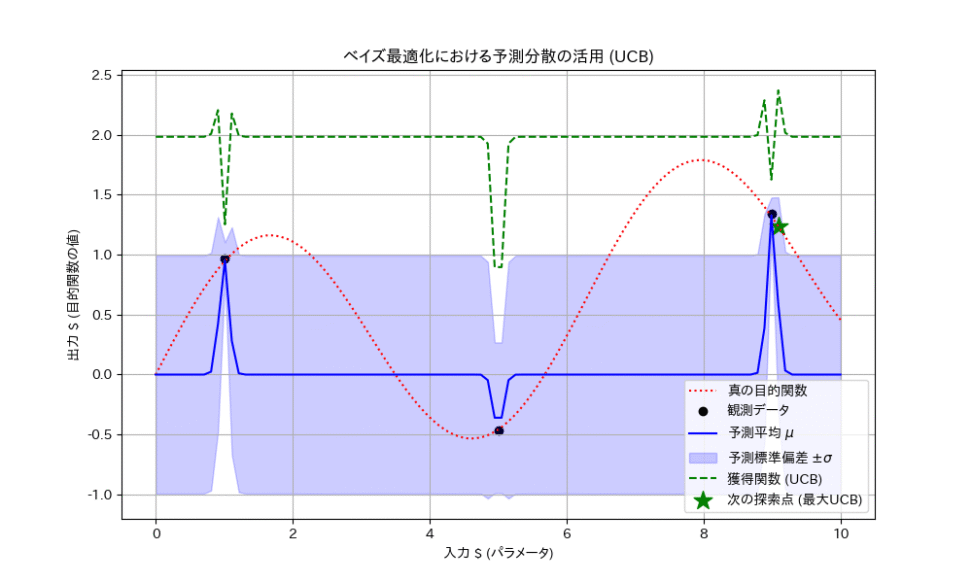
ベイズ最適化では、ガウス過程回帰を用いて、目的関数の予測モデルを構築します。そして、次にどのパラメータの組み合わせを試すべきか(どの実験をすべきか)を決定するために、以下の二つの指標を考慮します。
- 予測平均 $\mu_*$: 予測される目的関数の値が高い(良い結果が出そう)領域。
- 予測分散 $\sigma_*^2$: 予測の不確かさが大きい(まだよく分かっていない)領域。
この二つを組み合わせた獲得関数(Acquisition Function)を用いて、「最も良い結果が出そう」な場所と、「最も不確かさが大きく、新しい情報が得られそう」な場所のバランスを取りながら、次の探索点を決定します。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!






