【python】共分散分析(ANCOVA)の基礎から応用まで|因果推論
こんにちは、青の統計学です。
今回は交絡因子の影響を調整する共分散分析を解説しようと思います
共分散分析
共分散分析は、調整平均を用いて、共変量（covariate）の影響を考慮した上で、群間の平均値の差を検定する方法です。
分散分析（ANOVA）と似ていますが、共分散分析は共変量を考慮する点で異なります。
→これにより、分散分析より正確な分析ができます。
具体例｜交絡因子(confounding factor)を添えて
「相関は必ずしも因果とは限らない」という言葉はよく聞いていると思います。
その大きな要因が「交絡因子」と呼ばれる因子の存在です。具体例を見ていきましょう。
ある研究者は、ラジオ体操に来る人の健康状態を観察していくうち、「ラジオ体操に来ている人は将来寝たきりになる可能性が低い」と仮説を立てました。 では「ラジオ体操に行くこと」が「将来寝たきりになる可能性を下げる」と言えるでしょうか？
だめです。「もともとの健康状態」という交絡因子があります。
DAGを使ってみてみましょう。
DAG(Directed Acyclic Graph)
DAGは日本語で非巡回有向グラフといい、事象と事象を矢印で結び、因果関係と相関関係を整理していくグラフです。
上のラジオ体操と寝たきり状態の例を、DAGを使って整理してみましょう。
ラジオ体操に通う人はもともと健康意識が強く、普段の生活で健康に気を配っている可能性が高いです。
そうした人たちは、寝たきりになる可能性は当然低く、「寝たきりになる可能性」を下げた結果の原因の100%が、「ラジオ体操に通うこと」とは言えないのです。
DAGを描くと、「もともとの健康状態」が「ラジオ体操に通う可能性」と「寝たきりになる可能性」両者に影響を与える因子、つまり「交絡因子」であるとわかります。
こうした交絡因子があると、因果はなく、ただ相関があるだけの「疑似相関」という状態になります。
本当の因果関係を観察したい場合には、以下のような方法があります。
・RCT(ランダム比較化実験)
・影響の大きそうな交絡因子を定量的に求めて、影響を除外する。
今回解説する、「共分散分析」は後者の方法のうち、代表的な一つです。
交絡因子を一つ調整できるのが、共分散分析の嬉しいポイントです。
$$Y_{i}=β_{0}+β_{1}X_{i}+β_{2}R_{i}+ε_{i}$$
先ほどの例で言うと、「ラジオ体操に参加したグループ」と「ラジオ体操に参加していないグループ」 に分けて考えています。
ここでいうグループは、分散分析だと「水準」と呼んでいたものです。処置を受けているグループとそうでないグループに分けています。
ここでは2グループの識別のためにダミー変数を使います。
\(Y_i\): i番目のデータの目的変数
\(X_i\): i番目のデータの共変量
\(R_i\): i番目のデータの独立変数
\(ε_i\): i番目のデータの誤差
\(β_0\): 切片
\(β_1\): 独立変数の係数
\(β_2\): 共変量の係数
$$R_{i} \in{0,1}$$
仮にラジオ体操参加有無のダミー変数をRiと置いたときに、参加したグループはR=1、参加していないグループはR=0を取ります。
次に、説明変数Xは何であるかというと、「その人の健康指標」とします。
これが調整したい交絡因子でした。
例えば、被験者の健康具合をアンケートなどから10段階評価した値を入れます。
お気づきの方も多い方思いますが、共分散分析は、「ダミー変数(名義変数)を説明変数に加えた重回帰モデル」です。
t検定や分散分析に、回帰分析を混ぜたような考え方を使っています。
→つまりダミー変数（因子）と共変量（covariate）が目的変数に及ぼす影響を同時に考慮しながら、独立変数間の平均値の違いを検定する統計手法です。
共分散分析は、共変量を考慮することで、誤差のばらつきを減らし、独立変数間の効果の検出力を向上させることができます。
重回帰分析と共分散分析は、モデルとしては同じであるが、目的が異なっています。重回帰分析は回帰モデルの傾き\(β\)が目的です。
しかし共分散分析は、処置(ラジオ体操)の効果\(β2\)の評価であり、交絡因子(健康状態)はその助けになるように作られています。
共分散分析は2段階に工程を分けます。以下の工程に分けます。
①で元々の健康状態で、ラジオ体操に通うか否かへ与える影響を求めます。
その推定量の分だけ除き、残差だけ②で使います(重要)。
最後に、元々の健康状態の影響を除いた「ラジオ体操に通うか否か」が健康寿命に与える影響を②で求めます。
$$Y_{i}=β_{0}+β_{1}X_{i}+β_{2}R_{i}+ε_{i}$$
このモデルをもとに、独立変数Xと従属変数Yの関係を調べる際、共変量Xの影響を取り除きます。
そのために、共変量Rを調整した従属変数Y_adjを計算します。
$$Y_{adj} = Y – (β_1 * X_i)$$
これで「元々の健康状態」という交絡因子が除かれたことになりますね。
この\(Y_{adj}\)を使って、ANOVA（分散分析）を行い、独立変数X間の平均値の違いを検定します。
回帰直線を引きましたが、この回帰直線の縦方向の差を平均処置効果(ATE)と呼びます。
バイアスのほとんどは、実験の計画やデータの取り方で取り除く必要があります。
しかし、今回の共分散分析を使えば、一つだけですが交絡因子を「データを取った後に」調整することができます。
重回帰モデルを例にあげましたが、ロジスティック回帰分析やポアソン分析などの一般化線形モデルも同様に、説明変数と交絡因子をモデルに含めることにより、交絡因子の影響を排除した説明変数による目的変数の影響の有無やその大きさを推定することができます。
CODE|python
共分散分析をすべきかどうかは、データをしっかりみてから使ってください。
ここでは車の燃費データを使ってみます。
import pandas as pd
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
# MPGデータセットを読み込む
df = sns.load_dataset("mpg")
# 欠損値を削除
df = df.dropna()
# 従属変数(Y)、独立変数(X)、共変量(C)を選択
# 例: 目的変数 = 'mpg', 独立変数 = 'cylinders', 共変量 = 'weight'
Y = 'mpg'
X = 'cylinders'
R = 'weight'
# Categoricalな独立変数をダミー変数に変換
df[X] = df[X].astype('category')
df = pd.get_dummies(df, columns=[X], drop_first=True)
X_columns = [col for col in df.columns if X in col]
# ANCOVA モデルの式を作成
formula = f"{Y} ~ {' + '.join(X_columns)} + {R}"
# Statsmodels の ANCOVA モデルを実行
model = smf.ols(formula=formula, data=df).fit()
# 結果のサマリーを表示
print(model.summary())燃費への、シリンダー数(気筒数)の純粋な影響をみたいために重量という共変量を除きたいというモチベーションで共分散分析をします。
サマリーを出しました。指標について、いくつかご紹介します。
F-statistic: F統計量。モデル全体の統計的有意性を評価するために使用されます。この値が大きいほど、モデル全体が統計的に有意であることを示します。この例では、F統計量は203.4です。
Prob (F-statistic): F統計量に対応するp値。この値が小さい（通常は0.05以下）場合、モデル全体が統計的に有意であると判断できます。この例では、p値は8.34e-106であり、モデル全体が統計的に有意であることが示されています。
t: t統計量。各説明変数の係数が統計的に有意であるかどうかを評価するために使用されます。この値が大きいほど、対応する説明変数の係数が統計的に有意であることを示します。
P>|t|: t統計量に対応するp値。この値が小さい（通常は0.05以下）場合、対応する説明変数の係数が統計的に有意であると判断できます。この例では、すべての説明変数の係数は統計的に有意であることが示されています。
Omnibus: 正規性を検定するためのOmnibusテストの統計量です。この値が小さいほど、残差が正規分布に従うことが示唆されます。
Prob(Omnibus): Omnibusテストのp値。この値が大きい（通常は0.05以上）場合、残差が正規分布に従うことが示唆されます。この例では、p値は0.000であり、残差が正規分布に従わないことが示されています。
Durbin-Watson: 残差の自己相関を検出するためのDurbin-Watson統計量。通常、この値は0から4の範囲であり、2付近の値は残差間に自己相関がないことを示します。0に近い値は正の自己相関を、4に近い値は負の自己相関を示します。この例では、Durbin-Watson統計量は0.820であり、正の自己相関がある可能性が示されています。
Jarque-Bera (JB): Jarque-Bera検定統計量。これも残差が正規分布に従っているかどうかを検定するための検定です。この例では、Jarque-Bera検定統計量は96.400です。
Skew: 残差の歪度（skewness）。正規分布の場合、歪度は0に近い値を示します。正の歪度は右に伸びた分布を、負の歪度は左に伸びた分布を示します。この例では、歪度は0.805であり、残差が右に伸びた分布を示しています。
【統計検定2級で頻出】歪度と尖度を実例を通して解説|python&R
Note[2] は、条件数（condition number）が大きい（7.1e+04）ことを示しており、強い多重共線性（multicollinearity）や他の数値的な問題が存在する可能性があることを警告しています。
条件数が大きい場合、モデルが不安定になり、係数の推定値が不正確になる可能性があります。
多重共線性は、説明変数（独立変数や共変量）間に高い相関がある場合に発生します。
詳しくは以下のコンテンツをご覧ください。
【論文解説】多重共線性は回帰分析にどのような影響を与えるのか
補論：傾向スコアマッチングと回帰不連続デザインとの関係について
ここからは、共分散分析以外で因果推論を行う手法を紹介いたします。
特定の説明変数の回帰係数の値に興味があるというリサーチクエスチョンの場合、因果推論という手法が使われます。
$$Y_{i} = τD_{i}+f(X)+u_{i}$$
上の回帰式で言うと、\(τ\)が知りたい因果効果です。
そもそも、全ての回帰係数を正確に求めることは社会科学の分野では現実的ではないです。
さて、因果推論の手法として、他にも傾向スコアマッチングや回帰不連続デザインなどの手法があります。
傾向スコアマッチングとは、各サンプルが割り付けを受ける確率が他の説明変数に対して独立になるように、属性が近いサンプル同士に似た値になるように
「傾向スコア」と言う特徴量を加えます。
これによって、交絡因子によるバイアスを回避しようという目的があります。
一方、回帰不連続デザインとは、割り付けがある閾値を超えて行われる場合(例：テストの合格か不合格か)に使われる、閾値近傍のデータのみを使う回帰手法です。
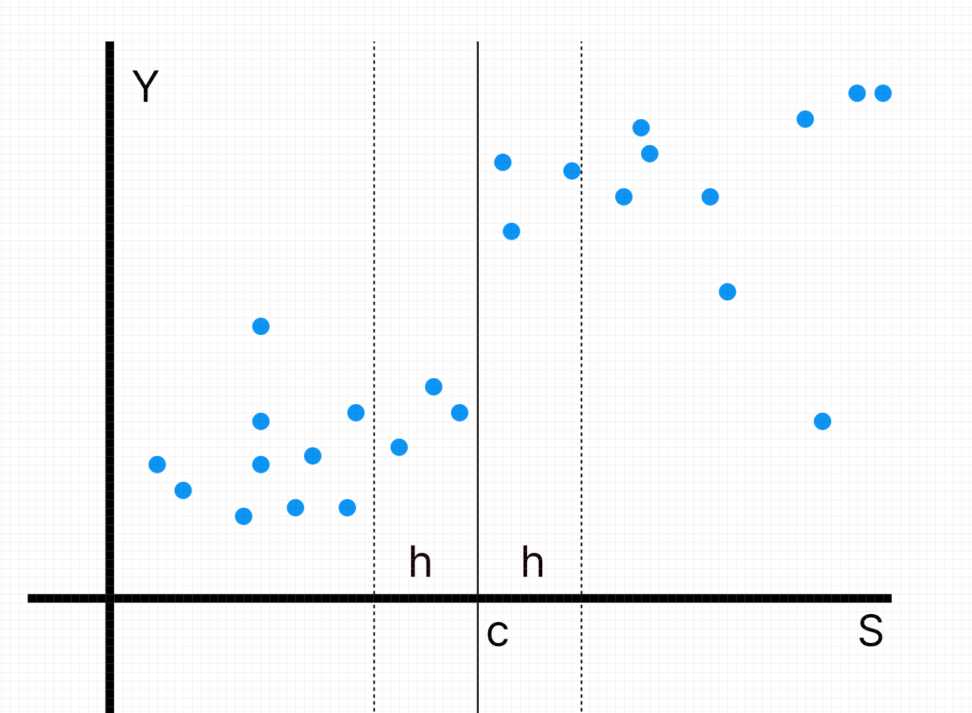
ギリギリ合格できなかった生徒と、合格最低点付近で合格できた生徒では、背景としての属性がほぼ同じであり、交絡因子の影響なしで割り付けが行われたと、解釈できると言うことです。
詳しくは以下のコンテンツをご覧ください。
【共変量の調整】傾向スコア・マッチングによる因果推論 | python
成田悠輔教授の論文でも使われた回帰不連続デザイン(RDD)を学ぶ|python
