【機械学習】決定木の仕組みと数学的背景をわかりやすく解説|線形回帰との違い
はじめに
さて、今回は決定木分析について解説いたします。
決定木分析の特徴を一言で言うと、直感的というか、私たちが日常的に行っている意思決定のプロセスを、そのままデータ分析のモデルとして再現しようとする手法です。

というのも、この手法の最大の魅力は、その解釈性の高さにあります。数式が複雑に絡み合うブラックボックスなモデルとは異なり、決定木は「もしXがYより大きければ、Zである」という明確なルール群として結果を提示します。
決定木系のアルゴリズムは、直感的でわかりやすく、データの尺度に左右されにくいことから様々な場面で応用されています。早速数学的な背景からみていきましょう
数学的背景:不純度について
この分析の核は、データをいかに「綺麗に」分けるか、という点に集約されます。
で、ここでいう「綺麗」とは、分割されたグループ(ノード)の中のデータが、すべて同じクラス(例えば「合格」か「不合格」か)に属している状態を指します。
この「混ざり具合」を定量的に評価するための指標が不純度(Impurity)です。
決定木は、この不純度を最も大きく減少させるような特徴量と分割点を、貪欲に(Greedy)選択し続けます。この不純度の指標として、主にジニ不純度とエントロピーの二つが用いられます。
色々と用語が出てきたので、ひとつずつ整理していきます。
ジニ不純度
ジニ不純度は、そのノードからランダムに選んだデータが、そのノードのクラス分布に基づいて誤って分類される確率を表します。値が小さいほど、ノード内のデータが単一のクラスに集中している、つまり「純粋」であることを意味します。
クラスが $k$ 種類あるとし、ノード $t$ におけるクラス $i$ のデータの割合を $p_i$ とすると、ジニ不純度 $G(t)$ は以下の式で定義されます。
$$G(t) = 1 – \sum_{i=1}^{k} p_i^2$$
例えば、ノードに「合格」が50人、「不合格」が50人いる場合($p_1=0.5, p_2=0.5$)、ジニ不純度は $1 – (0.5^2 + 0.5^2) = 0.5$ となり、最も不純な状態(混ざり合っている状態)を示します。一方、すべて「合格」の場合($p_1=1, p_2=0$)は $1 – (1^2 + 0^2) = 0$ となり、不純度はゼロ、つまり完全に純粋な状態です。
エントロピー (Entropy)
エントロピーは、情報理論の概念です。
ノード内のデータの不確実性や情報の乱雑さを測る尺度です。統計学の授業で「情報量」という言葉を聞いたことがあるかもしれませんが、エントロピーはその期待値に相当します。
ノード $t$ のエントロピー $H(t)$ は、以下の式で定義されます。
$$H(t) = – \sum_{i=1}^{k} p_i \log_2(p_i)$$
ジニ不純度と同様に、エントロピーも完全に純粋な状態($p_i=1$)で最小値の0を取り、最も混ざり合っている状態($p_i$が均等)で最大値を取ります。
情報利得
さて、決定木が実際に分割を行う際に利用するのは、分割によってどれだけ不純度が減少したかを示す情報利得 (Information Gain, IG)です。
あるノード $t$ を、特徴量 $A$ の値に基づいて二つの子ノード $t_L$ と $t_R$ に分割したとします。情報利得 $IG(t, A)$ は、分割前の不純度から、分割後の子ノードの不純度をデータ数で重み付けして引いた差として計算されます。
$$IG(t, A) = \text{Impurity}(t) – \left( \frac{N_L}{N} \text{Impurity}(t_L) + \frac{N_R}{N} \text{Impurity}(t_R) \right)$$
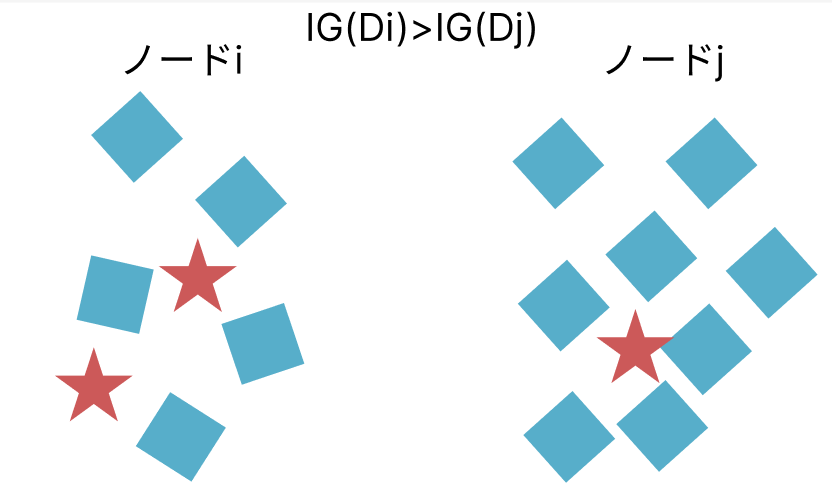
決定木アルゴリズムは、この情報利得を最大化するような特徴量 $A$ と分割点を、すべての候補の中から選択します。

つまり、決定木は「最も情報利得が大きい質問」を繰り返すことで、効率的にデータを分類しているのです。わかりやすくて助かりますね
さて、視覚的にもみていきましょう。
ジニ不純度、エントロピー、分類誤差のグラフを比較することで、これらの指標がどのように「混ざり具合」を表現しているかをみてみましょう。
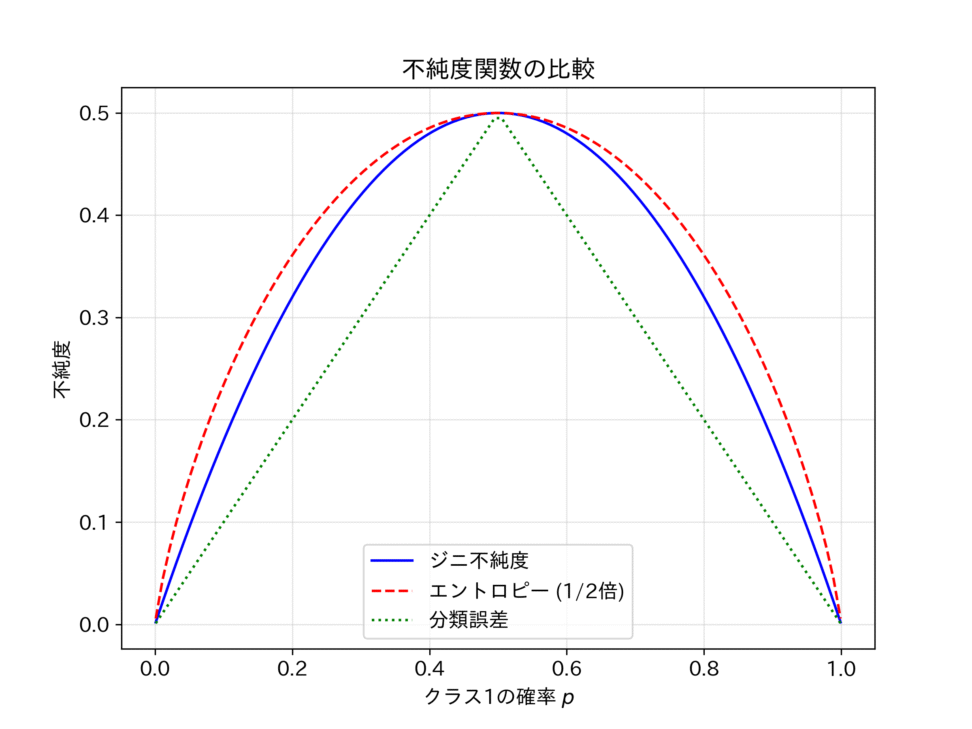
エントロピーが最も急峻なカーブを描き、ジニ不純度がそれに近い形状であることが分かります。
アルゴリズム詳細:CART法と再帰的分割
決定木を構築するアルゴリズムには、ID3、C4.5、そしてCART (Classification and Regression Trees)などがありますが、現代の機械学習ライブラリ(scikit-learnなど)で一般的に用いられているのは多分CART法です。
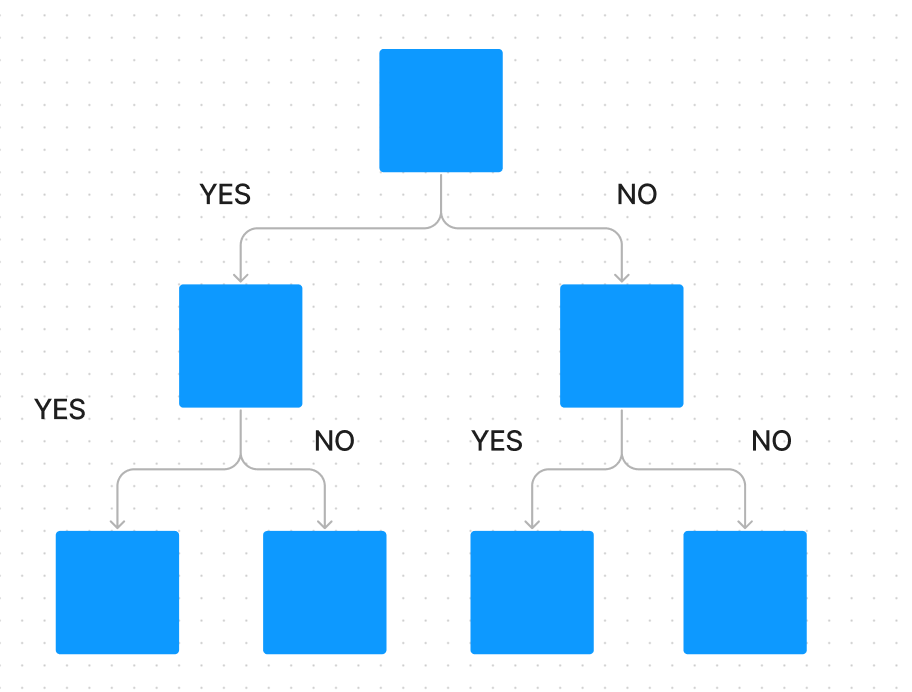
CART法の特徴は、常に二分木を生成することです。つまり、一つのノードから分岐する枝は、常に「Yes/No」の二つだけです。
分類木と回帰木
CART法は、目的変数(予測したい変数)がカテゴリ変数(例:合格/不合格)である場合は分類木として連続変数(例:住宅価格、気温)である場合は回帰木として機能します。
| 種類 | 目的変数 | 不純度の指標 | 分割の基準 |
| 分類木 | カテゴリ変数 | ジニ不純度、エントロピー | 情報利得の最大化 |
| 回帰木 | 連続変数 | 分散(Variance) | 分散減少量の最大化 |
回帰木の場合、不純度の代わりに分散を用います。ノード内のデータの分散が小さいほど、そのノードのデータは均質である(予測値が安定している)と見なされます。回帰木は、分割によってこの分散がどれだけ減少するか(分散減少量)を最大化するように分岐を決定します。
再帰的分割の仕組み
決定木の構築は、以下のステップを再帰的に繰り返すことで行われます。
- ノードの選択
- 現在のノード(最初は根ノード)を選択します。
- 最適な分割点の探索
- すべての特徴量と、その特徴量が取りうるすべての分割点(閾値)について、情報利得(または分散減少量)を計算します。
- 分割の実行
- 計算された情報利得が最大となる特徴量と分割点を選択し、ノードを二つの子ノードに分割します。
- 停止条件の確認
- 分割後の子ノードが以下のいずれかの条件を満たすまで、ステップ1〜3を繰り返します。
- ノード内のデータがすべて同じクラスになった(不純度が0)。
- ノード内のデータ数が最小限の閾値を下回った。
- 木の深さが最大値に達した。
- 分割後の子ノードが以下のいずれかの条件を満たすまで、ステップ1〜3を繰り返します。
このプロセスは、目の前のステップで最も良い結果(情報利得の最大化)を選ぶという点で、貪欲法(Greedy Algorithm)と呼ばれます。最適化のアルゴリズムでもこの呼ばれ方をするので覚えておくと良いと思います。
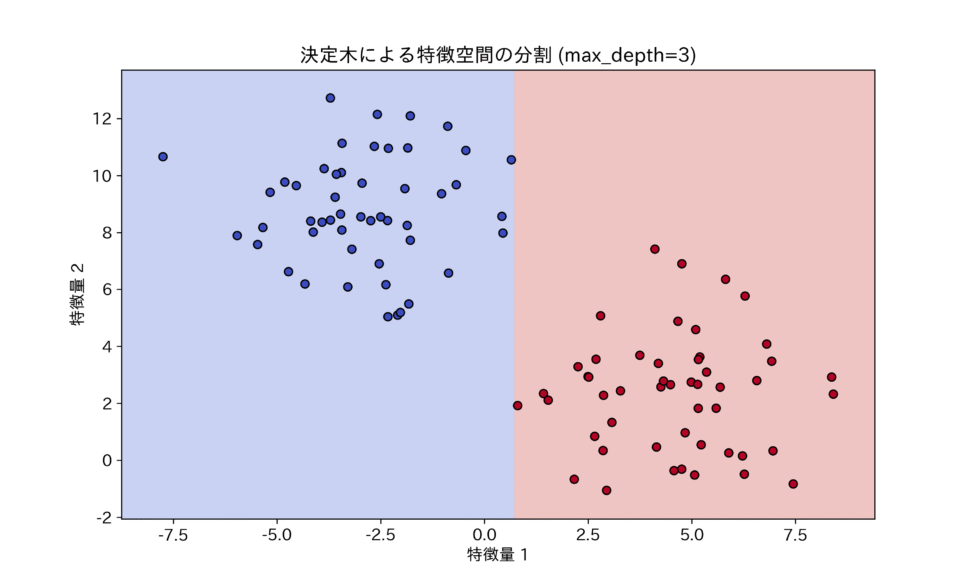
決定木がどのようにデータを分割しているかを視覚化すると、その仕組みがより明確になります。決定木は、常に特徴量の軸に平行な線で空間を区切っていくのが特徴です。
過学習と剪定の理論
決定木は、その性質上、過学習を起こしやすいモデルの代表格です。
なぜなら、停止条件を設定しなければ、データセット内の個々のデータポイントを完璧に分類しようと、際限なく枝分かれ(分岐)を続けてしまうからですね。
その結果、訓練データには完璧に適合するものの、未知のデータに対する予測精度が極端に低い、複雑すぎる木ができてしまいます。
この過学習を防ぎ、汎化性能を高めるために行われるのが剪定です。ネーミングがおしゃれです。
剪定には、木を成長させる前に深さやノード数を制限する事前剪定と、完全に成長させた後に不要な枝を切り落とす事後剪定があります。
コスト複雑性剪定
事後剪定の代表的な手法が、CART法で用いられるコスト複雑性剪定 です。これは、木の誤り率と木の複雑さの間に、適切なトレードオフを見つけることを目的としています。
ここで、新しいコスト関数 $R_\alpha(T)$ を導入します。
$$R_\alpha(T) = R(T) + \alpha |T|$$
- $R(T)$: 木 $T$ の誤り率(または回帰木の場合は二乗誤差)。
- 訓練データへの適合度を表します。
- $|T|$: 木 $T$ の葉ノード(終端ノード)の総数
- 木の複雑さを表します。
- $\alpha$: 複雑性パラメータ
- 木の複雑さに対するペナルティの度合いを調整します。
この式は、誤り率が低いほど良いが、木の複雑さ(葉の数)が増えるほどペナルティが加算されることを意味しています。
決定木分析では、このコスト関数 $R_\alpha(T)$ を最小化するような $\alpha$ の値を見つけ、その $\alpha$ に対応する最適な木を最終的なモデルとして採用します。$\alpha$ の値は、通常、交差検証(Cross-Validation)などの手法を用いて、汎化性能が最も高くなるように決定されます。

つまり、剪定とは、「訓練データへの適合度」と「モデルの単純さ」という二律背反のバランスを取るための、統計的な工夫なのです。
線形モデルとの対比
回帰分析やロジスティック回帰といった線形モデルは、データの特徴量と目的変数の間に線形(直線的)な関係を仮定します。これは、モデルの解釈が容易であるという大きな利点がありますが、現実の複雑なデータに潜む非線形な関係や特徴量間の交互作用を捉えることが苦手です。
一方、決定木は、線形な仮定を一切持ちません。
決定木は、常に軸に平行な線で空間を分割するため、データに斜めの境界線が潜んでいる場合、それを表現するために複雑な(深い)木を必要とします。

この図が示すように、決定木は非線形な関係を捉えるのは得意ですが、斜めの境界線のような特定の線形的な関係を表現するのには非効率的です。この特性こそが、決定木が他のモデルと組み合わされる理由の一つとなります。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!




