【アンサンブル学習】ブートストラップ法をpythonで実装|バギング
今回は、ブートストラップ法を使って推定器を複数作り、予測値を出してみます。
pythonでの実装になるので、Rでの実装に興味がある方は以下のコンテンツをご覧ください。
ブートストラップ法(bootstrap method)
社会科学の分野では、上記のように復元抽出を繰り返すことで、標準誤差を把握することにブートストラップ法は使われます。
今回は、主に機械学習の分野で使われる「データセットを複数作り、そこから作られるモデルを複数作成し、中間予測値を平均して、予測の改善を行う」手法に使われる、ブートストラップ法を扱います。
このような「予測の改善を行う」ためにブートストラップ法を使うことをバギングと呼びます。
ブートストラップ法は、統計学において、標本から推定する統計量の不確かさを評価するための方法です。
標本から無作為に抽出した複数の復元標本(ブートストラップ標本)を用いて、統計量を算出し、その分布を求めることで、統計量の不確かさを推定します。
標本数が少ない場合や、標本の分布が正規分布でない場合に有効で、不確かさの推定に用いられます。
一般的に、ブートストラップ法は以下のような手順で実行されます。
- 標本から復元抽出して、複数の復元標本を生成する。
- 各復元標本から統計量を算出する。
- 得られた統計量の分布を見ることで、統計量の不確かさを推定する
復元抽出について、おさらいをしましょう。
復元抽出とは、重複を許して抽出を行うことです。
[2,5,3,1,6,9,5,2,1,4,6]から5回復元抽出すると以下のような組み合わせが考えられます。 [2,3,3,3,3][5,5,5,5,5][1,4,6,9,5]...
-手順-
ブートストラップ法では、サンプルを復元抽出します。つまり擬似的に標本を母集団分布とみなし、独立同一リサンプリングを行います。
①n個の標本\({x_{1},…,X_{n}}\)からn個復元抽出を行います。それぞれの標本が抽出される確率は\(P(X=x_{i})= \frac{1}{n}\)です。
②これをB回繰り返し、n個のサンプルデータが入ったデータセットをB個用意します。
③B個のモデル(中間予測器)を作って、予測値を作ります。
-なぜ予測が改善するのか-
統計の基本的な知識があれば、復元抽出の回数を増やせば増やすほど、予測が改善することが理解できるはずです。
ここでは、同じ確率分布から抽出される確率変数を\(x_{b}\)とおいています。
$$x_{ave}={\frac{\sum_{b}x_{b}}{B}}$$
上は、ブートストラップ法によって算出した実現値の平均値です。
平均値の分散は以下のように表すことができます。
$$E[(x_{ave}-E[x_{ave}])^2] = {\frac{Var(x_{b})}{B}}+{\frac{B-1}{B}}×corr(x_{b},x_{b’})×Var(x_{b})$$
第1項は分散をブートストラップ回数でスケールしたものです。
\(X_{b}\)に関しては、同一分布から発生していますが、独立であるとは限らないので、相関が発生します。これが第2項です。
ブートストラップ法による復元抽出を繰り返すと、第1項は0に近づくことがわかりますね。これは大数の弱法則です。
ただし、第2項は残ったままです。つまり特徴量同士の相関は残ると言うことです。
そもそもモデルを作る際に使ったデータの分割の仕方によっては、大きくモデルが異なります。
また、ある特徴量を入れる/省くだけで大きくモデルが変わることもあります(ランダムフォレストで対処)。
ブートストラップ法は、いろんなサンプルデータを使ってモデルを平均化させることで、バイアスに対処するということです。
バギング、スタッキングなどの複数のモデルを組み合わせた機械学習の手法をアンサンブル学習と呼びます。
予測精度が上がるため、kaggleなどのデータ分析コンペでは、基本的にアンサンブル学習を使います。
とはいえ、アンサンブル学習はモデルの解釈が難しいため、ビジネスの分野で使って、非IT系の顧客に提案業務を行う場合には要注意です。
【SHAP】スタッキング(stacking)で特徴量の解釈はできるのか|pythonアンサンブル学習
ランダムフォレスト(random forest)との違いについて
ランダムフォレストとは、単にブートストラップ法で使う予測器に決定木アルゴリズムを使っているアルゴリズムではありません。
大きな特徴としては、予測器に決定木を使い、特徴量までもランダムに選択します。
→これにより、それぞれ多様な決定木を作成することができ、外れ値などに頑健なモデルを作ることができます。
ランダムフォレストに関しては、以下のコンテンツをご覧ください。
【ランダムフォレスト】ブートストラップ法を決定木に応用|python
CODE-ブートストラップ法をバギングに使った場合
今回はロジスティック回帰を推定器にして、複数推定量を作ります。
またデータセットは乳がんデータセットを使います。
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import BaggingClassifier
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import xgboost as xgb
cancer = load_breast_cancer()#データの読み込み
df_target = pd.DataFrame(cancer["target"], columns=["target"])
df_data = pd.DataFrame(cancer["data"], columns=cancer["feature_names"])
df = pd.concat([df_target, df_data], axis=1)データの読み込みです。
df.head()で以下のようなデータが出力されます。
| target | mean radius | mean texture | mean perimeter | mean area | mean smoothness | mean compactness | mean concavity | mean concave points | mean symmetry | … | worst radius | worst texture | worst perimeter | worst area | worst smoothness | worst compactness | worst concavity | worst concave points | worst symmetry | worst fractal dimension |
| 1.000000 | -0.730029 | -0.415185 | -0.742636 | -0.708984 | -0.358560 | -0.596534 | -0.696360 | -0.776614 | -0.330499 | … | -0.776454 | -0.456903 | -0.782914 | -0.733825 | -0.421465 | -0.590998 | -0.659610 | -0.793566 | -0.416294 | -0.323872 |
| -0.730029 | 1.000000 | 0.323782 | 0.997855 | 0.987357 | 0.170581 | 0.506124 | 0.676764 | 0.822529 | 0.147741 | … | 0.969539 | 0.297008 | 0.965137 | 0.941082 | 0.119616 | 0.413463 | 0.526911 | 0.744214 | 0.163953 | 0.007066 |
| -0.415185 | 0.323782 | 1.000000 | 0.329533 | 0.321086 | -0.023389 | 0.236702 | 0.302418 | 0.293464 | 0.071401 | … | 0.352573 | 0.912045 | 0.358040 | 0.343546 | 0.077503 | 0.277830 | 0.301025 | 0.295316 | 0.105008 | 0.119205 |
| -0.742636 | 0.997855 | 0.329533 | 1.000000 | 0.986507 | 0.207278 | 0.556936 | 0.716136 | 0.850977 | 0.183027 | … | 0.969476 | 0.303038 | 0.970387 | 0.941550 | 0.150549 | 0.455774 | 0.563879 | 0.771241 | 0.189115 | 0.051019 |
| -0.708984 | 0.987357 | 0.321086 | 0.986507 | 1.000000 | 0.177028 | 0.498502 | 0.685983 | 0.823269 | 0.151293 | … | 0.962746 | 0.287489 | 0.959120 | 0.959213 | 0.123523 | 0.390410 | 0.512606 | 0.722017 | 0.143570 | 0.003738 |
さて、データを目的変数と説明変数に分けて、教師データとテストデータに分けちゃいます。
y = df["target"]
X = df.loc[:, "mean radius":]
# 訓練データとテストデータに分ける
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=0)
#インスタンスを作成して、ブートストラップサンプルを作成する
bagging = BaggingClassifier(base_estimator=LogisticRegression(),n_estimators=100)
#学習
bagging.fit(X_train, y_train)ここではBaggingClassifier()というインスタンスを作ります。
引数estimatorに、ロジスティック回帰のインスタンスを渡します。ブートストラップ回数としては、n_estimators = 100を設定しています。
回数を増やせば増やすほど、予測の精度は良くなります(上述)が、計算量は大きくなります。
BaggingClassifier()の引数に関しては、以下が挙げられます。
base_estimator: データセットのランダムサブセットにフィットするestimator。 n_estimators: アンサンブル内のベースのestimatorの数。 max_samples: 各ベースのestimatorをトレーニングするためにXから選ぶサンプル数。 max_features: 各ベースのestimatorをトレーニングするためにXから選ぶ特徴量の数。 bootstrap: サンプルが置き換えられて抽出されるかどうか。 bootstrap_features: 特徴量が置き換えられて抽出されるかどうか。 oob_score: 外部バッグサンプルを使用して一般化精度を推定するかどうか。 warm_start: Trueに設定すると、以前のfit呼び出しの解を再利用してアンサンブルにより多くのestimatorを追加します。それ以外の場合は新しいアンサンブルをフィットします。 n_jobs: fitおよびpredict両方で並列に実行するジョブ数。 random_state: シャッフルデータ時に使用する仮想ランダム数生成器のシード。 verbose: 建設のverbosityを制御します。
# 予測確率を取得
y_pred = bagging.predict_proba(X_test)[:,1]
fpr, tpr, thresholds = roc_curve(y_test, y_pred)
# AUCの算出
auc = auc(fpr, tpr)
# ROC曲線の描画
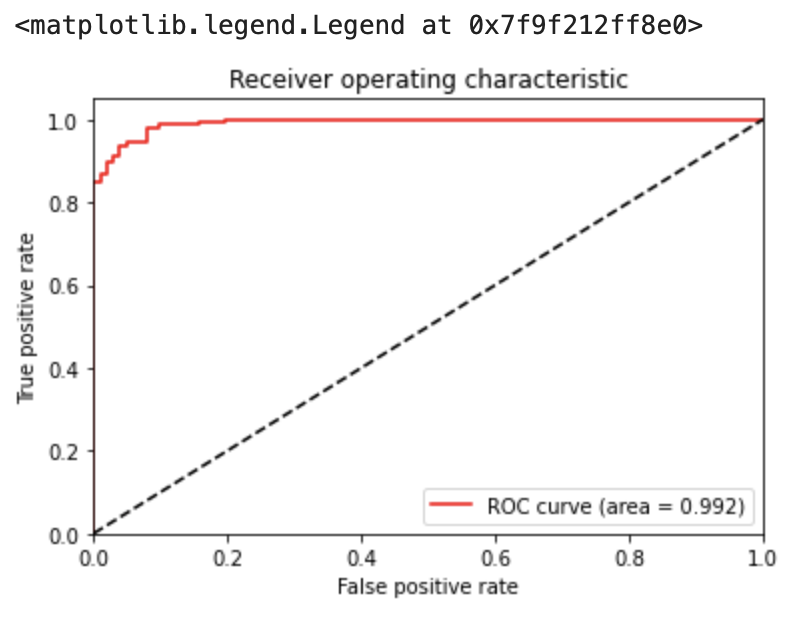
plt.plot(fpr, tpr, color='red', label='ROC curve (area = %.3f)' % auc)
plt.plot([0, 1], [0, 1], color='black', linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('Receiver operating characteristic')
plt.legend(loc="best")今回は、評価指標としてROC曲線を描画し、AUCを求めてみます。
AUCは位置に近いほうが良いとされます。
これらの指標に関しては、以下のコンテンツをご覧くださいませ。
【多変量解析】ROC曲線とAUCによる判別分析|python
CODE-resampleメソッドを使う場合
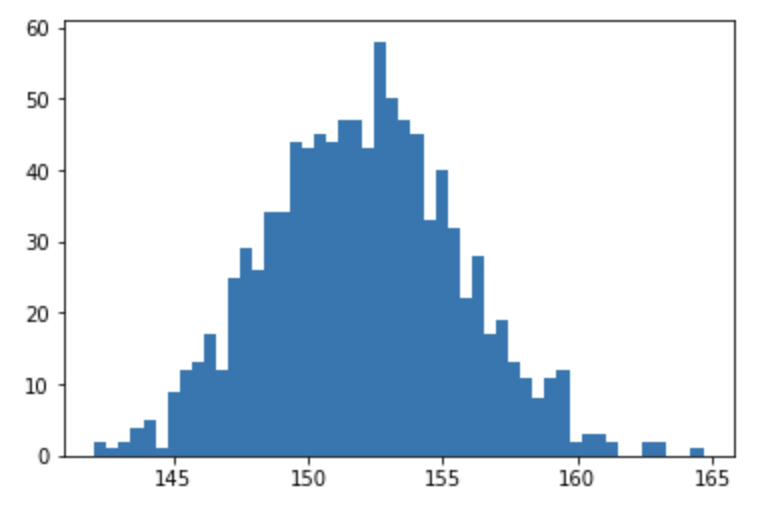
下記のコードでは、resample関数を使用して、標本から復元抽出したブートストラップ標本を生成し、それぞれから平均値を算出しています。
そして、それぞれの平均値の分布を見ることで、標本の平均値の不確かさを推定することができます。
from sklearn.utils import resample
from sklearn.datasets import load_diabetes
import numpy as np
import pandas as pd
diabetes = load_diabetes()
# Pandasによるデータの表示
df_target = pd.DataFrame(diabetes["target"], columns=["target"])
df_data = pd.DataFrame(diabetes["data"], columns=diabetes["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
# 標本データ
y = df["target"]
X = df.loc[:, "age":]
# ブートストラップ標本を生成
bootstrap_samples = [resample(y) for _ in range(1000)]
# 統計量を算出
mean_samples = [np.mean(s) for s in bootstrap_samples]
# 統計量の分布をプロット
plt.hist(mean_samples, bins=50)
plt.show()
データはscikit-learnの糖尿病のデータセットを使っています。
yという目的変数に関して復元抽出を行っております。
他の機械学習コンテンツについては以下をご覧ください。
【Sequential】Kerasを使ったニューラルネットワーク|python
【判別問題】サポートベクトルマシン(SVM)の仕組み|python

