【SHAP】特徴量重要度や寄与度、限界効果を意思決定者にうまく伝えたい話|python
これは直近仕事で抱えている問題を整理するために書き上げたコンテンツです。
今回は、prediction(予測)ではなくidentification(識別)に関する議論です。
kaggle等のコンペでは、予測に重きが置かれますが、ビジネスや研究の場では識別にも大きく関心が寄せられているのも事実です。
予測と識別の違い(difference between prediction & identification)
目的変数を精度よく予測するのが、主に機械学習の役割ですが、ビジネスの現場では、
「SEOに対して、サイト順位変動にもっとも影響を与える特徴量はどれだろうか。投資の優先度を決める参考のために、ランキング形式で教えてほしい。」
と言う意思決定者からの要望が来るかもしれません。
一方、研究の分野では、
「女性の就業率の変動に対し、保育所の整備促進は政策としてどの程度の因果効果があるのだろうか。」
というリサーチクエスチョンを立てるかもしれません。
こうした問題に対し、データサイエンスや機械学習に詳しくない意思決定者や周りの人に誤解なく数値を伝えるにはどのような指標を使えば良いでしょうか。
今回は、いくつかの指標を用いた、重要度・寄与度・限界効果などの算出方法について解説いたします。
特徴量重要度を提示する手法
特徴量重要度に関しては、決定木系のアルゴリズムで簡単に実装することができます。
決定木系のアルゴリズムに関しては、以下のコンテンツをご覧ください。
【XGB】交差検証法を使った勾配ブースティング決定木の実装|python
【ランダムフォレスト】ブートストラップ法を決定木に応用|python
【XGB】GridSearchを使いつつ特徴量重要度を知りたいッ‥!|python
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn import metrics
import numpy as np
from sklearn.ensemble import RandomForestClassifier
import matplotlib.pyplot as plt
# データセットのロード
data_breast_cancer = load_breast_cancer()
# Pandasによるデータの表示
df_target = pd.DataFrame(data_breast_cancer["target"], columns=["target"])
df_data = pd.DataFrame(data_breast_cancer["data"], columns=data_breast_cancer["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
y = df["target"]
X = df.loc[:, "mean radius":]
#教師データとテストデータの分割作業
X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.2, random_state=42)
seed=42
#グリッドサーチでハイパーパラメーターのチューニングを行う。
scores = {}
for max_depth in range(3, 10, 1):
for min_samples_leaf in range(2, 10, 1):
model = RandomForestClassifier(max_depth=max_depth,
min_samples_leaf=min_samples_leaf,
n_estimators=100,
random_state=seed
)
model.fit(X_train, y_train)
scores[(max_depth, min_samples_leaf)] = model.score(X_valid, y_valid)
# 検証結果をscoresに格納
scores = pd.Series(scores)
# 表示
print('ベストスコア:{:.2f}'.format(scores.max()))
print('その時のパラメータ(max_depth, min_samples_leaf):{}'.format(scores.idxmax()))
array_bst = np.array(scores.idxmax())
max_depth = array_bst[0]
min_samples_leaf = array_bst[1]
model_bst = RandomForestClassifier(max_depth=max_depth,
min_samples_leaf=min_samples_leaf,
n_estimators=100,
random_state=seed
)
model_bst.fit(X_train, y_train)
# 過学習確認
pred_rfc_class = model_bst.predict(X_valid)
pred_rfc_proba = model_bst.predict_proba(X_valid)[:, 1]
# 過学習確認
print("教師データ",model_bst.score(X_train, y_train))
print("テストスコア",model_bst.score(X_valid, y_valid))
#feature_importanceで特徴量重要度を算出する
feature = pd.DataFrame()
feature["columns"] = X.columns
feature["score"] = model_bst.feature_importances_
feature = feature.sort_values(by='score', ascending=False)
plt.figure(figsize=(50,12))
plt.plot(feature["columns"], feature["score"])
plt.title("feature_importance")
plt.show()ベストスコア:0.96 その時のパラメータ(max_depth, min_samples_leaf):(3, 2) 教師データ 0.9802197802197802 テストスコア 0.9649122807017544
以下のようなグラフが出力されたと思います。
特徴量が多いので横軸の特徴量の名前はつぶれて見えないですね。
パレートの法則
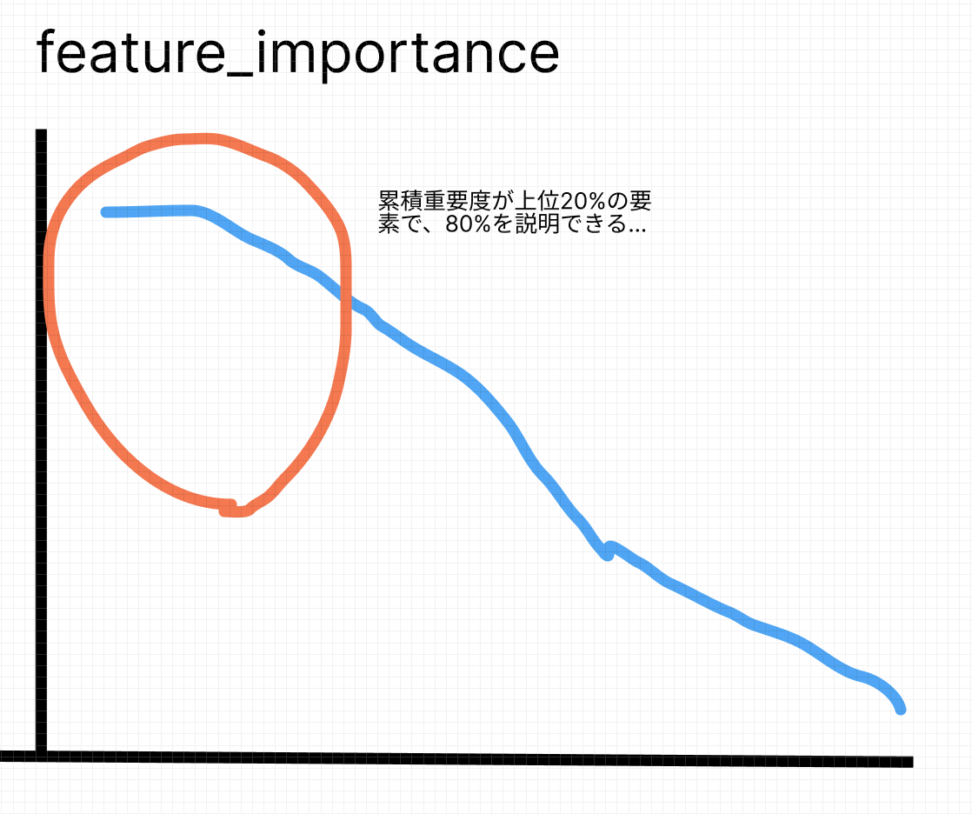
特徴量重要度を算出しましたが、重要度の低い説明変数は省きたいです。
この時使う経験則が、パレートの法則です。
「上位20%の特徴量で、全体の80%を説明できている」という考えです。
仮に上から累積重要度が、0.2近傍になるまで特徴量を数え上げたところ、以下の特徴量が重要そうです。
こちらを参考にして、上位20%の特徴量を重要と見なすのが定石ですが、まあ脳死で適用するのは微妙でしょう。
こちらのfeature_importanceは、決定木系のモデルがデータを振り分ける時に、獲得(gain)が一番大きい条件を作るために使う特徴量を「重要」と
評価しているだけであり、目的変数の増減に影響を与える重要度とはややずれます。
このため、「特徴量重要度が高いので、この説明変数に対してアプローチすると効率やインパクトが良い」などと説明するのは早計です。
後述するSHAP等を使って、多角的に特徴量に目を向けてから評価するのが吉です。
SHAPによる寄与度を提示する手法
SHAPとはsharply additive explanationsの略称であり、機械学習モデルの予測に対する解釈を行う手法です。
SHAP値は、各特徴量がモデルの予測にどの程度貢献しているかを示し、モデルの予測に対する全体的な理解を深めることができます。
前述した、特徴量重要度で予測結果を解釈しようとすると推測でしか解釈ができないため、現場での納得感が得られにくいということがあります。
SHAPではこうした問題に対処することができます。
早速ランダムフォレストのモデルを使って、SHAP値を算出します。
インストールしていない方は!pip install shap でインストールしておいてください。
import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingRegressor
import shap
# データの読み込み
boston = load_boston()
df_data = pd.DataFrame(boston.data, columns=boston.feature_names)
df_data['y'] = boston.target
seed = 42
X = df_data.drop(columns='y')
y = df_data['y'].tolist()
# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1)
# Gradient Boosting Decision Tree回帰モデルの構築
model = GradientBoostingRegressor(random_state=seed).fit(X_train, y_train)
# SHAP値の計算
explainer = shap.Explainer(model)
shap_values = explainer.shap_values(X_test)
#row_indexは0から行数-1まである。
shap_values = [shap_values[I] for i in range(len(X_test))]
# force_plotの作成
shap.initjs()
mean_shap_values = np.mean(shap_values, axis=0)
shap.force_plot(explainer.expected_value, shap_values = mean_shap_values, features = X_test.mean().values)
ボストン住宅価格のデータを使いました。モデルはGBDTを使っています。
まずSHAP値を計算しています。
SHAP値は、入力したデータセットと同じ数だけの次元となり、値が大きいほど予測値への貢献度が高くなります。
force_plotメソッドは、各サンプルごとの説明変数について、具体的な貢献度を可視化してくれます。
紹介するコードでは、1行ごとではなくテストデータのSHAP値を平均した貢献度を出力しています。
赤色が、目的変数の上昇に貢献した説明変数です。
青色が、目的変数の下降に貢献した説明変数です。
他にもsummary_plotやdependence_plotなどの可視化メソッドがあります。
データの次元数や目的に応じて使い分けてみましょう。
またSHAP値でのアプローチに限りませんが、
あくまで学習済みのモデルの振る舞いを解釈するので、モデル自体の精度がよくない場合は予期せぬ結果が出力されますので注意しましょう。
チューニングやきちんとした前処理、モデルの選択、交差検証などを丁寧に行なった上での分析です。
限界効果を提示する手法
ここでは、ロジスティック回帰を使って限界効果を算出するプログラムをご紹介します。
経済学を齧った方ならば理解が早いと思うのですが、限界効果とは「説明変数が1単位増えた時に何%目的変数が増減するか」の値です。
共線性が強いと信憑性が薄まるとの問題点はあります。
有意水準は以下のコンテンツに倣い、厳しくα=0.005としています。
【仮説検定】p値をゼロから解説(第一種の過誤,第二種の過誤,検出力)
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import scipy.stats as ss
#データの読み込み
df = load_breast_cancer()
df_data = pd.DataFrame(cancer.data, columns=cancer.feature_names)
df_data['y'] = cancer.target
seed = 42
X = df_data.drop(columns='y')
y = df_data['y'].tolist()
#教師データとテストデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=seed)
#ロジスティック回帰の実行
model = LogisticRegression().fit(X_train, y_train)
#限界効果を求める関数の作成
def calc_marginal_probability_effect(model, X, alpha=0.005):
#限界確率の算出
predict_values = model.predict_proba(X)[:, 1]
predict_values = predict_values * (1 - predict_values)
#限界効果の算出
mpe = np.tile(predict_values.reshape((-1, 1)), X.shape[1]) * model.coef_[0]
n = len(X)
#平均限界効果の算出
ampes = mpe.mean(axis=0)
#標準誤差の算出
stds = mpe.std(axis=0)
#t値の算出
t_values = ampes / (stds/np.sqrt(n-1))
#p値の算出
p_values = [1 - ss.t.cdf(x, df=n-1) if x > 0 else ss.t.cdf(x, df=n-1) for x in t_values]
t_ = ss.t.ppf(1-alpha/2, df=n-1)
uppers = ampes + t_ * (stds/np.sqrt(n-1))
lowers = ampes - t_ * (stds/np.sqrt(n-1))
return pd.DataFrame({
'colname' : X_data.columns.tolist(),
'coef' : model.coef_[0],
'ampe' : ampes,
'mpe_std' : stds,
't_value' : t_values,
'p_value' : p_values,
'lower_{:.3f}'.format(alpha/2) : lowers,
'upper_{:.3f}'.format(1-alpha/2) : uppers,
'significant' : ['*' if x <= alpha else '' for x in p_values]
})
result = calc_marginal_probability_effect(
model=model,
X=X_train,
alpha=0.005
)ロジスティック回帰の限界効果について解説します。
まず、ロジスティック回帰は以下の通りです。
$$f(x) = \frac{e^x}{1+e^x}$$
上の式は、目的変数Yが1になる確率を表します。
ここでは、\(X_{k}β_{k}\)による効果を表してみます。
微分の知識を使えば、限界確率効果(marginal probability effect)は以下のように表すことができますね。
$$MPE_{j}= \frac{\partial f(x)}{\partial x_{k}}=\frac{\partial f(x)}{\partial X_{i} \beta_{j}} \times \frac{\partial X_{i} \beta_{j}}{\partial x_{k}}$$
少しテクニカルですが、上のように限界確率効果は微分の積に表すことができます。
大文字の\(X\)は、ベクトルを表します。
-右側の\(\frac{∂X_{i}β_{j}}{∂x}\)について-
$$\frac{\partial X_{i} \beta_{j}}{\partial x_{k}} = \frac{(\beta_{1}X_{1}+…+\beta_{k}X_{k})}{\partial x}=\beta_{k}$$
x_{k}を項に持たないk-1個の項は全て0になりますよね。
-左側の\(\frac{∂f(x)}{∂X_{i}β_{j}}\)について-
こちらは、ロジスティック回帰の偏微分になります。
$$f'(x)=e^x \cdot \left(\frac{1}{1+e^x}\right)’ + e^x \cdot \left(\frac{1}{1+e^x}\right)’$$
$$f'(x)= \frac{e^x}{1+e^x}- (\frac{e^{2x}}{1+e^x})^2$$
$$f’(x)=\frac{e^x}{1+e^x}-(1-\frac{e^x}{1+e^x})=f(x)(1-f(x))$$
このように、結局簡単な積の形で表すことができます。
左側の式と右側の式を掛け合わせると、以下のようになります。
$$MPE_j = \frac{\partial f(x)}{\partial x_k} = f(x)(1-f(x))\beta_k$$
これが\(X_{k}β_{k}\)における限界確率効果です。
限界効果はサンプル数で平均する必要があります。
$$AMPE_{j} = \frac{1}{n} \sum_{i=1}^{n}f(x_{i})(1-f(x_{i}))β_{k}$$
上の式が限界効果になります。
さて、コードに関してですが、ampeに渡された値が、知りたい限界効果になります。
こちらは、説明変数が一単位増加すると、確率(説明変数)がどれだけ上がるかを表しています。
significantでは、有意水準0.005において有意かどうかを確認し、有意なら「*」を出力します。
脱線ですが、ミクロ経済学では、個人の消費行動の分析のために、財1単位あたりの消費による効用の増加量に注目します。
例えば、コーラの一杯目は効用が高いですが、2杯目以降は1杯あたりから得られる効用の増加はだんだんと減っていきますよね。
これを限界効用逓減の法則と呼びます。
目的変数と相関の強い説明変数を提示する手法
「相関が強いから影響がある」ということは大変リスクが大きいので、この手法だけを使うのはおすすめしません。
因果と相関は別だからですね。
ただ、重要度や寄与度が高い説明変数は、目的変数とも相関の強い部類でした!と多角的に評価するのは全然アリだと思います。
ここでは、糖尿病データを使い、目的変数であるtargetと相関係数の絶対値が高い順番に特徴量をリストに格納していくプログラムをご紹介します。
事前に交差項を作って、特徴量を増やしています。
交差項も合わせると、110個も特徴量ができたようです。
from sklearn.datasets import load_diabetes
import pandas as pd
diabetes = load_diabetes()
# 糖尿病データをDataFrame化
df_target = pd.DataFrame(diabetes["target"], columns=["target"])
df_data = pd.DataFrame(diabetes["data"], columns=diabetes["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
# 交差項のカラム名を作成
columns = df_data.columns.tolist()
cross = [col_1 + '_' + col_2 for col_1 in columns for col_2 in columns]
# 交差項のカラムを追加
for cross_col in cross:
df[cross_col] = df[cross_col.split("_")[0]] * df[cross_col.split("_")[1]]
# 特定の列のみに対して相関係数を計算
corr_values = df.corr()["target"].drop("target")
# 相関係数の絶対値が大きい順に並べる
corr_values = corr_values.abs().sort_values(ascending=False)
# 結果を表示
print(corr_values
以下のように出力されたと思います。
みた感じ、targetに相関が強い上位特徴量は、交差項ではない模様ですね。
bmi 0.586450
s5 0.565883
bp 0.441484
s4 0.430453
s3 0.394789
...
s2_s2 0.003852
s4_s3 0.003694
s3_s4 0.003694
s4_bp 0.003577
bp_s4 0.003577
Name: target, Length: 110, dtype: float64
交差項を作りましたが、デメリットとして解釈が難しくなります。
kaggleなどの予測に重きを置く場面では、交差項を大量に作成し、重要度が低いものをガシガシ削除していくというアプローチもありますが、
「結局、目的変数には何がどのくらい効くのか。因果関係はあるのか」という問いに対しては、やや説明が難しくなります。
主成分分析なども同じデメリットが挙げられますね。
【A/Bテストなし】競合施策の効果を推定したい|因果推論と時系列解析
フィッシャー情報量による特徴量選択をする手法
相関係数よりも精緻な方法として、フィッシャー情報量を使う方法もあります。
以下のコンテンツで詳しく解説していますが、ある特徴量が目的変数とどの程度強い関係性を持っているかを測定するために、確率分布がどの程度特徴量の変化に敏感か、を測る指標です。
【統計検定】フィッシャー情報量とクラメール・ラオの不等式について解説|python
今回は乳がんデータセットを使って、どの特徴量が比較的予測に重要なのかを考えます。
特徴量選択において、フィッシャー情報量は以下のような式で表されます。
$$I(x, y) = \sum_{c \in C} \sum_{v \in V} p(c, v) \log \frac{p(c, v)}{p(c)p(v)}$$
ここで、xは特徴量、yは目的変数、Cは目的変数のクラス、Vは特徴量の値の集合を表します。
p(c)はクラスcが出現する確率、p(v)は特徴量xが値vを取る確率、p(c, v)はクラスcが出現し、かつ特徴量xが値vを取る確率を表します。
この式は、特徴量と目的変数の同時分布と、それらの周辺分布を比較していることになります。
フィッシャー情報量は、特徴量xが目的変数yを予測する上での重要度を表す指標であり、値が大きいほど予測に役立つ特徴量であると言えます。
from sklearn.datasets import load_breast_cancer
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_classif
data = load_breast_cancer()
X, y = data.data, data.target
selector = SelectKBest(f_classif, k=10)
selector.fit(X, y)
selected_features = selector.get_support(indices=True)
print(data.feature_names[selected_features])['mean radius' 'mean texture' 'mean perimeter' 'mean area' 'mean concavity' 'radius error' 'perimeter error' 'area error' 'worst radius' 'worst perimeter']
SelectBestの引数kには、重要と判定された特徴量の出力個数を入力します。
ここでは10個にしています。乳がんデータセットの特徴量が30個くらいなので、上位1/3の重要な特徴量のみを抽出していることになります。
具体的には、フィッシャー情報量を用いた特徴量選択では、すべての特徴量についてフィッシャー情報量を計算しています。
予測に対して「重要」とは
フィッシャー情報量を用いた特徴量選択において、「重要」というのは、特徴量が目的変数と強い関係性を持っているということです。
つまり、ある特徴量が目的変数を予測する上で重要であるということは、その特徴量を使うことで予測精度が向上する可能性が高いということです。
例えば、乳がんデータセットにおいては、特定の腫瘍の大きさや形状、細胞核の形態、クロマチンの存在などの特徴量ががんの種類(良性か悪性か)を予測する上で重要であることが知られています。
フィッシャー情報量を用いた特徴量選択によって、これらの特徴量を選択することで、より正確ながんの診断が可能となります。
他にも嬉しいこととしては、重要な特徴量を選択することで、モデルの学習に必要な情報の量が減り、計算時間やメモリ使用量を削減できる場合もあります。
また、不要な特徴量を除外することで、モデルの過学習を防ぎ、汎化性能を向上させることもできます。
過学習の話で余談ですが、パラメータが増えるとテスト誤差は大きくなるというのが一般的だったのが、Transformerを使ったLLMにはスケール則という、データやパラメータ、計算資源を増やせばテスト誤差が下がるという話があり、この辺りの原理がまだまだわかっていません。
→我々の脳の神経細胞も2000億くらいニューロンがあり、1個のニューロンも1万個くらいのシナプスによって構成されており、モデルで例えるととても大きいです。LLMは我々の知能に近づいてきたということでしょうか、非常に興味深いです。
相関関係による特徴量の選択と何が違うのか
目的変数との相関関係とフィッシャー情報量による特徴量選択とは、微妙に異なる概念です。
-相関関係-
相関関係とは、2つの変数がどの程度同じ傾向を持っているかを表す指標です。
例えば、ある特徴量が大きくなると目的変数も大きくなる場合、これらの変数は正の相関があると言います。
逆に、ある特徴量が大きくなると目的変数が小さくなる場合、これらの変数は負の相関があると言います。
【外れ値に対処】順位相関係数と相関係数の違いについて | python
-フィッシャー情報量-
一方、フィッシャー情報量による特徴量選択は、ある特徴量が目的変数とどの程度強い関係性を持っているかを測定するための方法です。
フィッシャー情報量は、2つの確率分布がどの程度異なるかを表す指標であり、特徴量の取りうる値が目的変数を分類するための重要な情報を提供することができます。
つまり、相関関係は2つの変数の関係を表す指標であり、特徴量選択においても重要な指標ではあります。
しかしフィッシャー情報量は、特定の特徴量が目的変数と強く関連しているかどうかを評価するためのより精密な指標となります。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


