【共変量の調整】傾向スコア・マッチングによる因果推論 | python
こんにちは、青の統計学です。今回は傾向スコアをご紹介します。
因果推論に必要な考え方ですので、しっかり習得しましょう。
傾向スコア (propensity score)
傾向スコアとは、群間比較研究において、介入を受けたグループと受けなかったグループの間のバイアスを補正するために用いられるスコアです。
観察研究において介入効果を推定する際に、治療群と比較群を類似にするために用いられます。
つまり、傾向スコアを使うことで、治療群と比較群の間の混乱因子の影響を除去し、より正確な結果を得ることができます。
傾向スコアとは、「処置とコントロール群以外の条件を同じにしたい」というモチベーションから考えられます。
以下の例を考えてみましょう。
新薬には血圧を下げる効果があるのかどうかを調べたいです。 健康状態や年齢がバラバラの被験者50人連れてきて、新薬を飲むか飲まないかを自分で決めてもらいます。 (こちらが、新薬を投与するかしないかを指定する(ランダム)と倫理的に問題があるからです。) 処置群の血圧の変化から、コントロール群の血圧の変化を除いた時に、新薬の効果はわかるでしょうか？
答えとしては、微妙です。
微妙な理由としては、血圧に影響を与える影響のある、「年齢」や「健康状態」がバラバラだからです。
これらを共変量と言います。
この属性の違いにより、本人が新薬を使うかどうかを選択する可能性が変わります。
若くて健康状態の良い人がコントロール群に選び、比較的年をとっていて健康状態が良くない人が処置群に選ばれる傾向がありそうです。
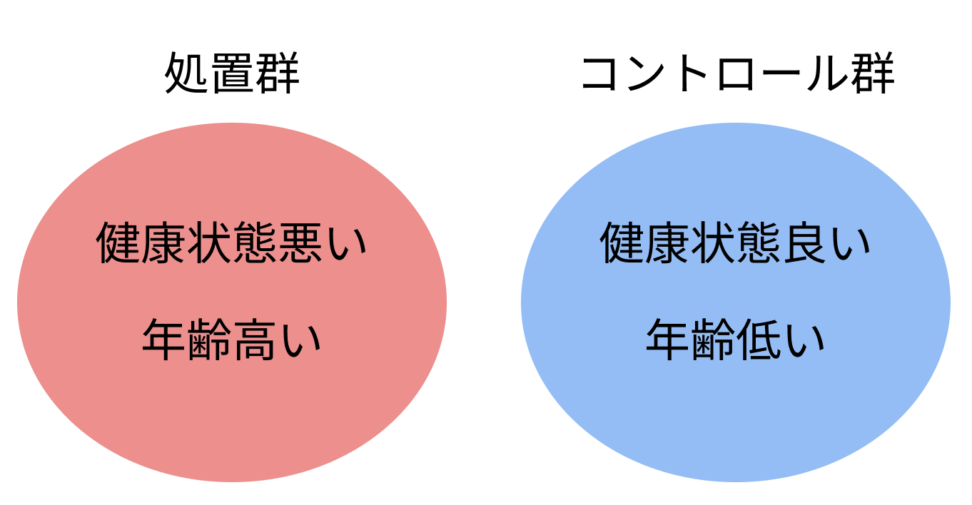
差の差分析によって得られる、新薬の介入効果が全くの出鱈目であるということはわかると思います。
この時に傾向スコアを使います。
当然処置群とコントロール群では、属性が似通っている方が因果効果を正確に測れますよね。
この属性(交絡因子)の「似通い度」を傾向スコアと呼んでいるわけです。
もう少し正確に言えば、傾向スコアとは「各サンプルが介入を受ける確率」のことです。
求め方としては、ロジスティック回帰や決定木、深層学習などで各サンプルのもつ観測された共変量を説明変数、介入の有無を目的変数に置くことで求められます。
利点の一つとして、目的変数の確率分布を考えなくて良い、ノンパラメトリックな手法であることです(後で詳しく解説いたします)
まとめると、傾向スコアは、介入を受けたグループと受けなかったグループの間の交絡因子の影響を排除するために、共変量を調整する方法として用いられます。
(共変量とは、介入と結果の間に関係があると考えられる変数のことで、例えば、年齢、性別、BMI、既往症などが挙げられます。)
傾向スコアを使うことで、共変量を用いた多重回帰分析によって、介入効果をより正確に推定することができます。
*健康状態や年齢は事前にある程度揃えて実験しろというのが真っ当な意見です。
今回は、「処置の有無以外の条件を被験者で一緒にしたいよね」というのが傾向スコアのモチベーションであると理解してもらえると嬉しいです。
定理|theorem
ここでは、傾向スコアの定理を紹介します。
傾向スコアとは共変量Xが与えられた時の処置に割り付けられる確率を意味します。
$$e(X)=Pr(T_{i}=1|X)$$
ここの割り付け確率の表し方にはいろいろやり方などがございます。
決定木系のアルゴリズムや深層学習、ロジスティック回帰などで表せます。
例えば、割り付け確率はロジスティック回帰の累積分布関数で表すことができます。
定理1：バランシング
処置の割り付けTと観測された共変量Xは、傾向スコアe(X)が与えられた時の条件付き独立です。
$$X\perp T|e(X)$$
定理2：条件付き独立性
傾向スコアe(X)が与えられると、潜在的結果変数{γ(1),γ(0)}と処置の割り付けTは条件付き独立です。
$$(γ(1),γ(0))\perp T|e(X)$$
これは、つまり処置と結果変数が関連していないということです。
同じ傾向スコアならば、処置を受ける確率は同じです。
注意点として、傾向スコアによるモデリングでは処置の割り付けに影響を与えるものは観測された共変量Xのみであり、未観測の共変量によるバランシングまでは補償していません。
バランシング 共変量Xの関数b(X)が与えられた時のXの条件づき分布が、処置群とコントロール群で同じになること。
つまり、傾向スコアとは「傾向スコアが同じだと、期待される目的変数は同じであるという便利な統計量」ということがわかりました。
CODE
先ほどの例を使います。
全て架空のデータになっております。現実には全く即していないのでご了承ください。
| health | blood pressure | age | intervention | |
| 0 | 10 | 2.31 | 25 | 0 |
| 1 | 6 | 1.44 | 30 | 1 |
| 2 | 6 | 5.50 | 29 | 1 |
| 3 | 7 | 2.07 | 30 | 0 |
| 4 | 6 | 4.00 | 28 | 1 |
health：健康指標。10に近づくほど健康。 blood pressure：介入(コントロールでも可)前後の血圧の変化量(負の数)。 age：年齢 intervention：被験者が介入を受けたかどうかのダミー変数。0なら介入がなく、1なら介入がある。
ライブラリのインポートを行います。
先ほど表に書いたデータを読み込んでデータフレームにしてみましょう。
import numpy as np
import pandas as pd
import statsmodels.api as sm
df = pd.read_csv("health.csv")
# 傾向スコアを算出するために使用する説明変数
X = df[["health","age"]]
X = sm.add_constant(X)
# 介入変数
D = df["intervention"]Xを傾向スコアを算出するために使用する説明変数とします。
今回交絡因子となりそうなのは、「健康状態」と「年齢」が挙げられます。
また、介入変数として、「新薬の投与有無」のinterventionを与えます。
つまり、介入が行われるかどうかは、健康状態や年齢の影響を受けるということです。
# 傾向スコアを算出
model = sm.Logit(D, X)
result = model.fit()
result.predict(X)
df["傾向スコア"] = result.predict(X)
df.head()先ほども説明いたしましたが、傾向スコアとは「介入を受ける確率」です。
傾向スコアをロジスティック回帰を使って推定します。
50人の被験者に対し、以下のような傾向スコアが与えられました。
傾向スコアが近いほど、介入を受ける確率(今回で言うと、新薬を自分で試す確率)が近くなります。
| health | blood pressure | age | intervention | 傾向スコア | |
| 0 | 10 | 2.31 | 25 | 0 | 0.078998 |
| 1 | 6 | 1.44 | 30 | 1 | 0.512202 |
| 2 | 6 | 5.50 | 29 | 1 | 0.497296 |
| 3 | 7 | 2.07 | 30 | 0 | 0.376869 |
| 4 | 6 | 4.00 | 28 | 1 | 0.482395 |
平均処置効果(Average Treatment Effect)
応用として、傾向スコアを用いたマッチングまで行おうと思います。
傾向スコアを算出するだけではなく、マッチングまで行わなければ意味はありません。
ここで求める値は、平均処置効果(ATE)と呼ばれるものです。
【ゼロから始める】統計的因果推論とは。で個別個体効果を説明しましたが、個別個体効果は直接求めることはできません。
注目されるのは、平均処置効果の方です。
$$ATT = E(Y_{1}-Y_{0}|Z=1)$$
これは介入群における平均処置効果です。
$$ATU = E(Y_{1}-Y_{0}|Z=0)$$
これはコントロール群における平均処置効果です。
介入前後による血圧の変化の期待値が、介入群における平均処置効果です。
一方、コントロール前後(要は何もしない)の変化の期待値が、コントロール群における平均処置効果です。
そして、実験の目的である「新薬の効果」とはATTからATUを除いた平均処置効果です。
これを関数を作って求めてみます。
差の差分析と同じ考え方ですね。
$$ATE = E(Y_{1}-Y_{0})-E(Y_{1}-Y_{0}|Z=0)$$
# 平均処置効果を求める
def calc_match_ate(df, step=0.1):
scores = np.arange(0, 1, step)
match_arr = np.array([])
for score in scores:
_df = df[(df["傾向スコア"]>=score) & (df["傾向スコア"]<score+step)]
tmp0 = np.array(_df[_df["intervention"]==0]["blood pressure"])
tmp1 = np.array(_df[_df["intervention"]==1]["blood pressure"])
if (tmp0.size!=0) and (tmp1.size!=0):
match_arr = np.append(match_arr, tmp1.mean() - tmp0.mean())
return match_arr.mean()
calc_match_ate(df, step=0.1)>0.61994047619047620.619940476‥くらい純粋な効果が見込める。と言うことがわかりました。
ノンパラメトリック手法
傾向スコアは、ノンパラメトリック手法と言われます。
ノンパラメトリック手法は、パラメトリック手法と違い、目的変数の確率分布が分からなくても良いです。
正しいモデルをわかっていれば、共分散分析は有効です。
しかし、「モデルがわからない」かつ「共変量を置いて、線形関係を仮定したときに明らかに望ましくない」場合にノンパラメトリック手法を使います。
線形性の過程が必要な共分散分析について知りたい方は、【交絡を解決!?】共分散分析(ANCOVA)とは一体何なのか。をご覧ください。
ランダムな割り付け(ランダム比較化実験など)ができればいいのですが、例えばマーケティングのABテスト(新しいモーダルを見せるor見せない)だと、半数には見せないので毀損が生じる可能性があります。
また、今回の例で取り上げた新薬の例では、「半数には血圧を下げる効果があると思われる薬を投与しないのか」という倫理的な問題が生じます。
こうしたABテストなどを実施できない時には、介入以外による影響のバイアスを否定できず、介入効果を過大もしくは過小に評価してしまう恐れがあります。
こんな時に傾向スコアを使うと便利です。
傾向スコアによる解析は準実験と呼ばれます。
準実験とは、処置の無作為な割り付けがない観察研修でも割り付けや比較対象の集団についてなんらかの統制を行うことで無作為化実験を真似するデザインであり、社会科学系でよく使われることが多いです。
回帰不連続デザイン(regression discontinuity design)
また、ある閾値において介入と非介入をキッパリと分ける自然実験などに対しては、回帰不連続デザインという手法が使われます。
例として、テストの合格か不合格かで入る学校が変わり、学校自体の教育効果はあるのか知りたいという場合などです。
テストの合格によるある学校への入学が介入となります。
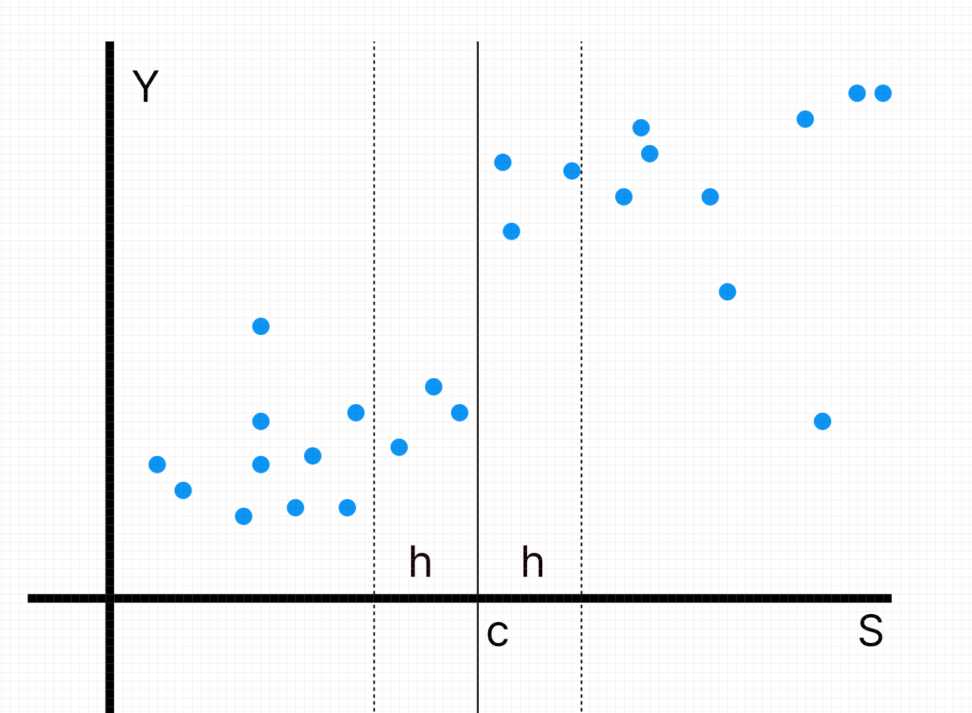
合格最低点を境目にして、3年後の学力(縦軸)に差があれば、学校による教育効果が示唆されます。
データの取り方や交絡因子の除き方に関して、議論があるので詳しくは以下のコンテンツをご覧ください。
成田悠輔教授の論文でも使われた回帰不連続デザイン(RDD)を学ぶ|python
【A/Bテストなし】競合施策の効果を推定したい|因果推論と時系列解析
青の統計学では、社会科学のうち計量経済学を取り扱っています。
詳しくは、計量経済学をご覧くださいませ。
まとめ|傾向スコアの評価方法や注意点について
傾向スコアは、介入を受けたグループと受けなかったグループの共変量の差を調整するための方法であり、比較研究において広く用いられています。
傾向スコアの求め方には、重回帰分析、ロジスティック回帰、機械学習などの方法があります。
比較研究には注意が必要ですが、適切に用いることで、より正確な結果を得ることができます。
-傾向スコアの評価方法-
傾向スコアを用いた比較研究においては、傾向スコアの適切性を評価することが重要です。傾向スコアの適切性を評価するためには、以下のような方法があります。
① 標準化平均偏差の比較 傾向スコアによって調整した治療群と比較群の標準化平均偏差を比較し、その差が小さいほど、傾向スコアの調整効果が高いと言えます。
② 標準化バイアスの比較 傾向スコアによって調整した治療群と比較群の間の標準化バイアスを比較する方法があります。
標準化バイアスが小さいほど、傾向スコアの調整効果が高いと言えます。
-傾向スコアの注意点-
傾向スコアを用いた比較研究においては、以下のような注意点があります。
① 傾向スコアを用いた分析は、共変量が完全に観察されている場合に限定されます。
共変量が欠落している場合は、その影響を排除できないため、結果にバイアスが生じる可能性があります。
② 傾向スコアには、介入を受けるかどうかに影響を与えない共変量だけを用いることが望ましいです。
介入に影響を与える共変量を含めてしまうと、傾向スコアの調整効果が低下する可能性があります。
③ 傾向スコアを用いた分析において、傾向スコアの分布が均一であることが望ましいです。
傾向スコアの分布に偏りがある場合、調整効果が不十分になる可能性があります。
