差の差分析(DID)をわかりやすく解説:多期間DIDとサンプルサイズ計算まで
こんにちは、青の統計学です
今回は、実務でもよく使われる「差の差分析」について解説いたします。社会科学系の授業でも紹介されますね。シンプルで理解しやすいかつ強力な分析手法ですが、並行トレンドの仮定など前提となるルールもあります。
デジタルマーケティングでの応用例もご紹介します。
【前提知識】因果推論とは
まずは、因果推論について理解しましょう。
DIDについて知りたい方は、すっ飛ばしても構いません。
さて、因果推論とは、「AがBの原因にちゃんとなっているかどうか」を統計学的なアプローチで考えていくことです。
日々使う、「原因」と「結果」に対して少し向き合って、
「本当に因果関係があるのか?」
「相関関係があるだけではないのか?」
と考え直す学問のカテゴリーになります。そして、因果関係があると認められた事象に対しては、実際の政策や医療に活かしていくという実学でもあります。「そもそも因果とは何か?」のように、因果の哲学的な意味を深ぼるような学問ではありません。

因果推論は、例えば「集団食中毒の原因を明らかにする」といった、比較的緊急性の高い「疫学」の分野から発展してきました。いち早く病の原因や、どんな薬が病気に有効なのかということを解明したいというモチベーションが、因果関係の追求につながってきました。
因果推論の応用範囲
因果推論の応用範囲はかなり広く、計量経済学や心理学、医学、経済政策などに応用されています。経済政策の予算は限られているので、「とりあえず給付金配ればいいでしょ」「しっかりした証拠はないけど保育園を建てよう」などできないわけです。

ちなみに、証拠に基づいた政策立案のことをEBPM(evidence based policy making)といい、近年日本の政界でも検討されつつあります。
因果推論の大きな特徴として、反事実仮想というもがあります。
特徴ではありながら、一方で解決するのが困難なものです。
反実仮想の具体例
「ある化粧品のテレビCMを一年間流した。一年後の化粧品の売上は1,000万円だった。この時、CMはどの程度売上に貢献したでしょうか」
この問題には、「テレビCMを流さなかった場合の一年後の売り上げ高」が必要になります。このような、「現実とは別の実現し得ない場合」を反事実と言います。
そして反事実仮想モデルは、観測された事実(手元のデータ)と観測されなかった反事実の比較によって因果を定義していくアプローチを取ります。
CMの効果=(1年間CMを出した売上)-(CMを出さなかった売上)
この第二項が反事実であり、当然ですが直接計算は行えませんね。
潜在的結果変数と平均処置効果について
先ほどの具体例を一般化します。
$$Y_i = T_{i}Y_i^1+(1-T_{i})Y_{i}^0$$
T:処置をおこなったかどうかの変数。処置がある場合は、1を取り、ない場合は0を取ります。
Yi(左辺):個体iについて、観測された結果変数(これが知りたい)
*上の具体例でいうと、CMを打ち出したことによる効果
右辺の\(Y^1\)と\(Y_0\)を潜在的結果変数と言います。
- Y(1):処置をおこなった場合(CMを出した)の、潜在的な結果
- Y(0):処置を行わない場合の(CMを出さない)の、潜在的な結果
いずれか一方しか観測することができません。
これは、因果推論の根本的な問題点である言えます。
| 商材id | 売上(2021)(X) | 売上(2022)(Y) | 処置の有無(T) | Y-X |
| 1 | 600 | 653 | 1 | 53 |
| 2 | 361 | 380 | 0 | 19 |
| 3 | 490 | 503 | 1 | 13 |
| 4 | 189 | 300 | 1 | 111 |
上の例でも分かるとおり、各商材について「処置をおこなった場合のY」か「処置をおこなわなかった場合のY」の一方しかわかりません。
$$τ_{i}=Y_{i}^1-Y_{i}^0$$
この差を個体個別効果(indivisual causal effect)と言います。
もちろん一方は反実仮想になるので直接計算はできません。
平均処置効果は、個体個別効果の平均値として定義されます。
すべての個体の個別効果を合計し、個体の数で割ることで計算できます。
数式で表すと以下のようになります。
$$ATE=\frac{1}{N}\sum_{i}^{N}τ_{i}$$
実際の研究においては、すべての個体に対する個別効果を直接観測することはできません。
そのため、RCT(ランダム化比較試験)や、観察データに基づく因果推論手法(例えば、傾向スコアマッチングや重み付き回帰など)を用いて、平均処置効果を推定します。
以上のように、潜在的結果変数モデルとして因果関係を扱う流派を「Rubin流」と言います。
相対するPerl流よりも計算が楽という特徴があります。観測データではないものに注目するという点においては共通しています。
1. 差の差分析(DID)とは?
さて、本題に入ります
1.1 DIDの直感的理解
DIDは、その名の通り「2つの差」を比較します。具体的には、以下の4つの平均値を比較します。
- 介入群の介入後の平均値
- 介入群の介入前の平均値
- 対照群の介入後の平均値
- 対照群の介入前の平均値
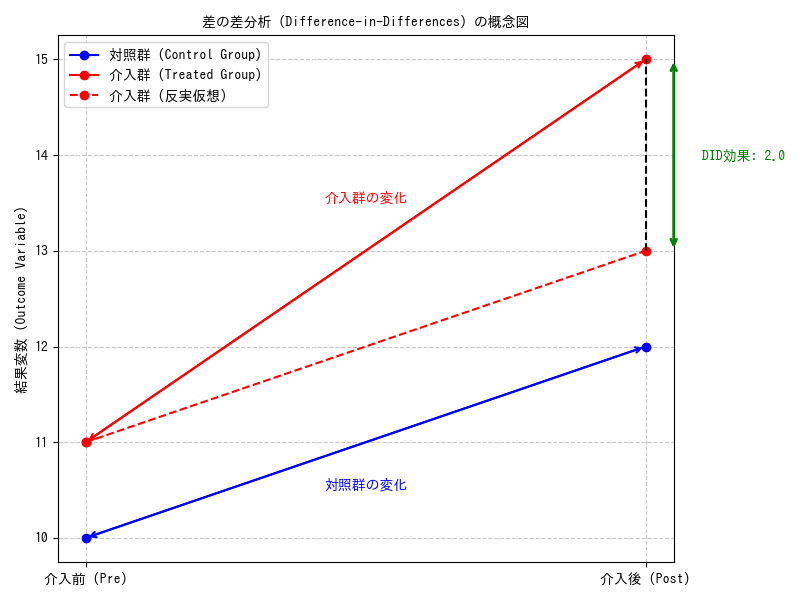
まず、介入群と対照群それぞれの介入前後の変化(差)を計算します。そして、介入群の変化から対照群の変化を差し引くことで、介入の純粋な効果を推定します。つまり、
$$\text{DID効果} = (\text{介入群の介入後の平均値} – \text{介入群の介入前の平均値}) – (\text{対照群の介入後の平均値} – \text{対照群の介入前の平均値})$$
これは、介入群で観測された変化のうち、介入とは関係なく対照群でも発生したであろう変化を差し引くことで、介入固有の効果を分離する考え方です。
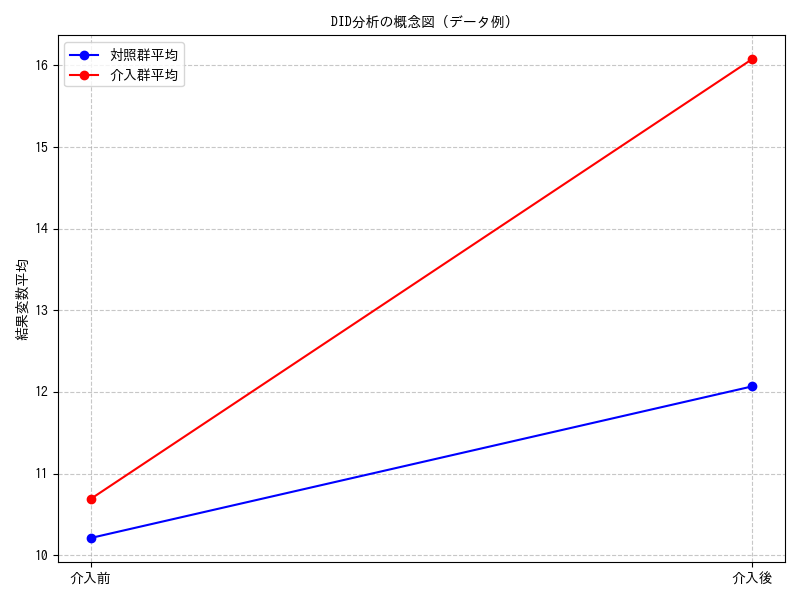

経済学の古典的な研究であるCard and Krueger (1994) の例では、ニュージャージー州の最低賃金引き上げが雇用に与える影響を、隣接するペンシルベニア州を対照群として分析しました。DIDは、介入群が介入を受けなかった場合の反実仮想の状態を、対照群の変化をベースに推測するアプローチになります。
図で理解
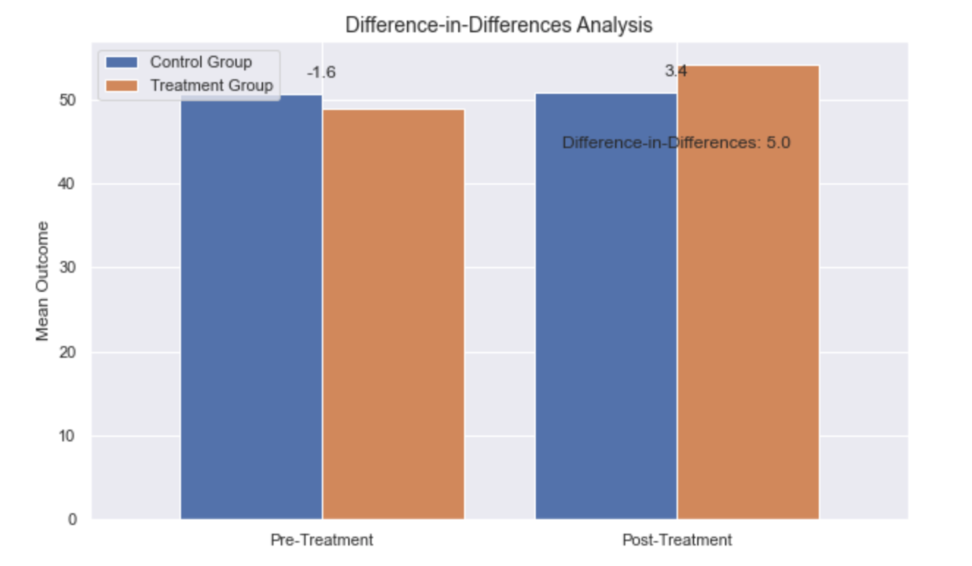
上のように、処置を施したグループをオレンジ/コントロール群を青色としています。
処置前の棒グラフと処置後の棒グラフを比べると処置群のアウトカムがコントロール群よりも大きく伸びていると思います。
ではどれほど処置の効果があるかというと、以下のような処置群内での差とコントロール群内での差の差をとることで表せます。
1.2 DIDの数学的背景:平均処置効果(ATT)の推定
DIDは、介入を受けたグループにおける平均処置効果を推定します。ATTは、介入を受けた個体が、もし介入を受けなかった場合の反実仮想の結果と比較して、実際に介入を受けたことでどれだけの効果があったかを示します。
数学的には、各個体 $i$ と時点 $t$ において、潜在的結果変数 $Y_{i,t}(1)$(介入を受けた場合)と $Y_{i,t}(0)$(介入を受けなかった場合)を用いて定義されます。観測される結果変数 $Y_{i,t}$ は、介入群ダミー $D_i$(介入群なら1、対照群なら0)と介入後ダミー $T_t$(介入後なら1、介入前なら0)を用いて以下のように表されます。
$$Y_{i,t} = D_i Y_{i,t}(1) + (1 – D_i) Y_{i,t}(0)$$
DIDが推定したいATTは、介入群における介入後の効果であり、時点を介入後 ($t=2$) と介入前 ($t=1$) の2期間とすると、以下のように定義されます。
$$\text{ATT} = E[Y_{i,2}(1) – Y_{i,2}(0) | D_i = 1]$$
$E[\cdot | D_i = 1]$ は介入群における期待値を意味します。$Y_{i,2}(0)$(介入群が介入を受けなかった場合の介入後の結果)は観測できないため、DIDは特定の仮定の下でこれを観測可能なデータで置き換えます。
1.3 平行トレンド仮定
DIDが因果効果を正確に推定するための最も重要な仮定が、平行トレンド仮定(Parallel Trends Assumption)です。この仮定は、「もし介入がなかったとしたら、介入群と対照群の平均的な結果は時間とともに平行に推移したであろう」というものです。数学的には、
$$E[Y_{i,2}(0) – Y_{i,1}(0) | D_i = 1] = E[Y_{i,2}(0) – Y_{i,1}(0) | D_i = 0]$$
と表されます。これは、「介入がなかった場合の介入群の介入前後の変化」と「対照群の介入前後の変化」が等しいことを意味します。対照群は介入を受けていないため、$Y_{i,t}(0)$ がそのまま観測されます。
したがって、この仮定は、観測可能なデータを用いて以下のように書き換えることができます。
$$E[Y_{i,2}(0) – Y_{i,1} | D_i = 1] = E[Y_{i,2} – Y_{i,1} | D_i = 0]$$
この仮定は検証することができません。介入前のデータを用いて、この仮定が「もっともらしい」かどうかを間接的に検証するプレテストやイベントスタディのプレトレンド部分の確認が重要です。介入前の期間でトレンドが平行であれば、介入後もそのトレンドが継続したであろうという説得力が高まります。
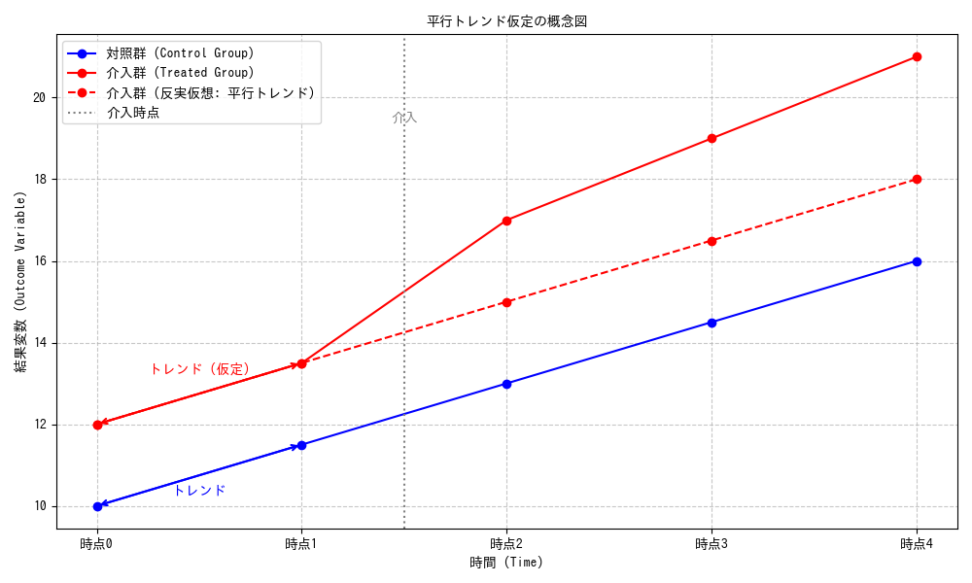

並行トレンドの仮定は、処置群と対照群の処置前の平均アウトカム(結果)の傾向が一致することを意味します。言い換えると、もし処置がなかった場合、処置群と対照群は同じ傾向で推移していたはずであるという仮定です。
→処置群とコントロール群をどれだけランダムに選べているかも関わってきますね。例えば、薬の影響を知りたいときに体調の悪い人間の集団を処置群にし、体調の良い人間の集団をコントロール群にしてもうまく平均処置効果は出せず、因果関係とは到底言えないということですね。
1.4 OLSによるDIDの推定
DID効果は、重回帰分析(OLS)を用いて推定できます。基本的なDIDモデルは以下の回帰式で表されます。
$$Y_{i,t} = \beta_0 + \beta_1 D_i + \beta_2 T_t + \beta_3 (D_i \times T_t) + \epsilon_{i,t}$$
- $Y_{i,t}$:個体 $i$ の時点 $t$ における結果変数
- $D_i$:介入群を示すダミー変数(介入群なら1、対照群なら0)
- $T_t$:介入後を示すダミー変数(介入後なら1、介入前なら0)
- $D_i \times T_t$:介入群かつ介入後を示す交互作用項
- $\epsilon_{i,t}$:誤差項
このモデルにおける各係数の解釈は以下の通りです。
- $\beta_0$:対照群の介入前の平均値
- $\beta_1$:介入群と対照群の介入前の差 ($E[Y_{i,1} | D_i=1] – E[Y_{i,1} | D_i=0]$)
- $\beta_2$:対照群の介入前後の変化 ($E[Y_{i,2} | D_i=0] – E[Y_{i,1} | D_i=0]$)
- $\beta_3$:DID効果(ATT)
特に重要なのは交互作用項の係数 $\beta_3$ です。この係数は、介入群の介入前後の変化から、対照群の介入前後の変化を差し引いた値、まさにDID効果を表しています。つまり、
$$\beta_3 = (E[Y_{i,2} | D_i=1] – E[Y_{i,1} | D_i=1]) – (E[Y_{i,2} | D_i=0] – E[Y_{i,1} | D_i=0])$$
OLSモデルを用いることで、DID効果を直接推定し、その統計的有意性を評価できます。
このOLSモデルは、Two-way Fixed Effects (TWFE) モデルのシンプルな形と解釈できます。TWFEモデルは、個体ごとの固定効果 $\alpha_i$ と時点ごとの固定効果 $\phi_t$ を導入し、観測されない特性や共通のトレンドをコントロールします。
$$Y_{i,t} = \alpha_i + \phi_t + \delta D_{i,t} + \epsilon_{i,t}$$
こ$D_{i,t}$ は介入群かつ介入後である場合に1となるダミー変数です。
このモデルにおける $\delta$ がDID効果に相当します。TWFEモデルは、より複雑なデータ構造(例えば、複数期間にわたるパネルデータ)に対応できるため、DID分析において広く用いられています。
2. 多期間DID
2.1 軸の拡張とイベントスタディ
実際のデータは複数期間にわたることが多く、DIDのフレームワークを多期間に拡張した多期間DIDが用いられます。これにより、介入効果の時間的変化や、介入が異なるタイミングで発生する状況に対応できます。
多期間DIDのOLSモデルは、以下のように表現できます。
$$Y_{i,t} = \alpha_i + \phi_t + \sum_{k=-K}^{M} \delta_k I(t = t_0 + k) \cdot D_i + \epsilon_{i,t}$$
- $t_0$ は介入時点
- $I(t = t_0 + k)$ はイベント時間 $k$ を示すダミー変数
- $\delta_k$ はイベント時間 $k$ におけるATT
*通常、イベント時間 $k=-1$ を参照カテゴリとし、$\delta_{-1}=0$ と設定します
特定のイベント(介入)前後で変数がどう変化したかを時系列で分析する手法です。DIDの文脈では、介入時点を「イベント発生時点」と捉え、イベント発生前後の各期間における介入効果(ATT)を推定します
これをイベントスタディ(Event Study)と言います。

各 $\delta_k$ は「処置を受けてから $k$ 期間目に処置群がどれだけ変わったか(対照群に比べて)」を表します。$k<0$(リード)は事前のトレンド(プレトレンド)、$k\ge0$(ラグ)は動的効果を示します。ただ、プレトレンドがゼロ付近 → 平行トレンド仮定が支持されやすく、因果解釈がしやすくなる。ただし「プレトレンドがゼロだから完璧」とは限りません
3. DIDのサンプルサイズ推定
個体レベルで処置がランダム化されている(個人/セッション単位)、かつ 2期間(前後)で観測 する最も基本的なケースをご紹介します。
3.1 仮定
- 各群は等しい人数 $n$ を持つ(処置群・対照群)。
- 各個体の結果の分散を $\sigma^2$ とする。
- 同一個体の前後相関(テスト-再テスト相関)を $\rho$ とする。
- 検出したい平均効果(DIDで検出したい差)を $\delta$ とする。
- 有意水準 $\alpha$、検出力 $1-\beta$ を用いる。
3.2 分散の導出
1個体の差 $Y_{i,2}-Y_{i,1}$ の分散は
${\mathrm{Var}(Y_2 – Y_1) = 2\sigma^2 (1-\rho).}$
群平均の差の分散(各群の平均):
$${\mathrm{Var}(\overline{\Delta Y}) = \dfrac{2\sigma^2(1-\rho)}{n}.}$$
DID(処置群の差 − 対照群の差)の分散(等分散・独立群の仮定):
$${\mathrm{Var}(\widehat{\mathrm{DID}})=\dfrac{2\sigma^2(1-\rho)}{n} + \dfrac{2\sigma^2(1-\rho)}{n} = \dfrac{4\sigma^2(1-\rho)}{n}.}$$
よって標準誤差は
$${\mathrm{SE} = 2\sigma \sqrt{\dfrac{1-\rho}{n}}.}$$
3.3 必要サンプル数 $n$(群ごと)
有意水準 $\alpha$、パワー $1-\beta$ の下で、片側/両側に応じた臨界値を $z_{1-\alpha/2}$ と $z_{1-\beta}$ とすると、
$${\dfrac{\delta}{\mathrm{SE}} = z_{1-\alpha/2} + z_{1-\beta}}$$
を満たす必要があり、これを $n$ について解くと
$${\boxed{n ;=; \dfrac{4\sigma^2(1-\rho), (z_{1-\alpha/2}+z_{1-\beta})^2}{\delta^2}}.}$$

直感的解釈としては、前後の相関 $\rho$ が高いと(つまり同じユーザーの行動が安定していると)必要サンプル数は小さくなります。効果サイズ $\delta$ が大きければ当然少ない人数で検出可能です。
3.4 標準化して使う
効果の標準化サイズを $d=\delta/\sigma$(Cohen’s d の類)とすると、
$${n = 4(1-\rho)(z_{1-\alpha/2}+z_{1-\beta})^2 / d^2.}$$
これで事前に過去データから $\rho$ と $d$ を推定しておけば、必要サンプル数がすぐに計算できます。
4. DIDの結果の有意性確認
4.1直感(何を検定しているか)
当然ですが、DID の推定値 ${\widehat{\mathrm{DID}}}$ は「処置前後の差(処置群)− 処置前後の差(対照群)」です。
有意性検定では帰無仮説を
${H_0: \mathrm{DID} = 0}$(処置に効果はない)として、観測された ${\widehat{\mathrm{DID}}}$ が偶然かどうかを調べます。
4.2シンプルな数式(2期間・2群の例)
各群・各時点でのサンプル平均を
- 処置群(Treatment)前:${\bar Y_{T,pre}}$
- 処置群後:${\bar Y_{T,post}}$
- 対照群(Control)前:${\bar Y_{C,pre}}$
- 対照群後:${\bar Y_{C,post}}$
DID は
$${\displaystyle \widehat{\mathrm{DID}} = (\bar Y_{T,post}-\bar Y_{T,pre}) – (\bar Y_{C,post}-\bar Y_{C,pre}).}$$
分散(=標準誤差の二乗)は、各平均の分散を合成して求めます。各セル(群×時点)を独立とみなす単純ケースで、各セルの平均の分散が ${\mathrm{Var}(\bar Y)=\dfrac{s^2}{n}}$($s^2$ は各セルの分散、$n$ は各セルのサンプル数)であれば
- 各群の差(post − pre)の分散は ${\dfrac{s^2}{n} + \dfrac{s^2}{n} = \dfrac{2s^2}{n}}$。
- DID の分散は両群の差の分散の和なので ${\dfrac{2s^2}{n} + \dfrac{2s^2}{n} = \dfrac{4s^2}{n}}$。
したがって標準誤差は
$${\displaystyle \mathrm{SE}(\widehat{\mathrm{DID}})=\sqrt{\dfrac{4s^2}{n}} = 2s/\sqrt{n}.}$$
(注:上の導出は「各セルの観測が独立」かつ「各セルで同じ分散 $s^2$」という単純化の下でのものです。。)
検定統計量は通常の $t$ 統計量:
$${t = \dfrac{\widehat{\mathrm{DID}}}{\mathrm{SE}(\widehat{\mathrm{DID}})}.}$$
4.3 数値例
次のような観測値があるとします(とても単純な例):
- 処置群:前期平均 ${\bar Y_{T,pre}} = 5$,後期平均 ${\bar Y_{T,post}} = 8$
- 対照群:前期平均 ${\bar Y_{C,pre}} = 4$,後期平均 ${\bar Y_{C,post}} = 5$
- 各セルのサンプル数 ${n=50}$,各セルの分散(標本分散)を同じく ${s^2=16}$(標準偏差 $s=4$)と仮定
まず DID:
$${\widehat{\mathrm{DID}} = (8-5) – (5-4) = 2.}$$
各セルの平均の分散:
$${\mathrm{Var}(\bar Y)=\dfrac{s^2}{n}=\dfrac{16}{50}=0.32.}$$
各群の差(post−pre)の分散
$${0.32+0.32=0.64.}$$
DID の分散(両群の差の和)
$${0.64+0.64=1.28.}$$
標準誤差:
$${\mathrm{SE}=\sqrt{1.28}\approx 1.1314.}$$
$t$ 統計量:
$${t = \dfrac{2}{1.1314}\approx 1.7678.}$$
両側検定の p 値(大標本・正規近似)
$${p \approx 0.0771.}$$
→ 有意水準 ${\alpha=0.05}$ では 棄却できない(つまり「統計的に有意」ではない)が、弱い有意性の領域(p ≈ 0.077)に近い、という結論になります。
どう解釈する??
この例では観測された DID は 2(単位) ですが、サンプルのばらつきが大きいため($s=4$)、その信頼性は高くありません。p=0.077 は「偶然である可能性が約7.7%」という意味合いです。
- サンプル数を増やす、または分散を下げる(ノイズを取り除く)と有意性は改善し得ます。
- もしデータがパネル(同一個体を追跡)であれば、前後の相関を考慮した分散式を使うべき(より小さいSEになる可能性あり)。
- クラスタ構造がある場合はクラスタロバストSEや wild cluster bootstrap を使う必要があります(通常の SE だと過小評価されやすい)。
CODE
差の差分析を行うpythonコードをご紹介します。
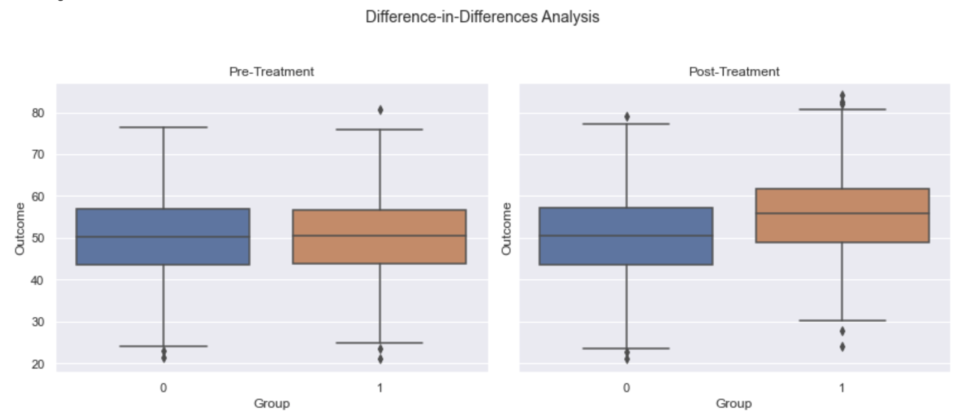
データを生成して、箱ひげ図で平均処置効果を観察します。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.formula.api as smf
# データの生成
np.random.seed(42)
n = 1000
treated = np.random.choice([0, 1], size=n)
pre_treatment = np.random.normal(50, 10, size=n)
post_treatment = pre_treatment + np.where(treated, 5, 0) + np.random.normal(0, 2, size=n)
data = pd.DataFrame({
'id': np.arange(n),
'treated': treated,
'pre_treatment': pre_treatment,
'post_treatment': post_treatment
})
# 差の差分析
data_long = pd.melt(data, id_vars=['id', 'treated'], var_name='time', value_name='outcome')
data_long['post'] = (data_long['time'] == 'post_treatment').astype(int)
model = smf.ols('outcome ~ treated * post', data=data_long)
results = model.fit()
print(results.summary())
# 平均処置効果
ate = results.params['treated:post']
print(f"Average Treatment Effect: {ate:.2f}")
# データの可視化
sns.set(style='darkgrid')
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), sharey=True)
sns.boxplot(x='treated', y='pre_treatment', data=data, ax=ax1)
sns.boxplot(x='treated', y='post_treatment', data=data, ax=ax2)
ax1.set_title('Pre-Treatment')
ax2.set_title('Post-Treatment')
ax1.set_xlabel('Group')
ax2.set_xlabel('Group')
ax1.set_ylabel('Outcome')
ax2.set_ylabel('Outcome')
plt.suptitle('Difference-in-Differences Analysis', fontsize=14, y=1.03)
plt.tight_layout()
plt.show()treated = np.random.choice([0, 1], size=n)で 0(対照群)と1(処置群)から成る処置(treated)の配列をランダムに生成します。
バイアスのないようにデータを生成します。
data_long = pd.melt(data, id_vars=[‘id’, ‘treated’], var_name=’time’, value_name=’outcome’)
meltメソッドはpivotメソッドの逆で、横持ちのデータフレームを縦持ちに変えてくれます。
データフレームの再構成のために使用します。
df:対象となるデータフレーム id_vars:IDとして利用する変数(カラム) value_vars:melt する変数(カラム)、無指定の場合はid_vars以外の変数全部 var_name:variable変数の変数(カラム)名、無指定の場合はvariableが変数(カラム)名になる value_name:value変数の変数(カラム)名、無指定の場合はvalueが変数(カラム)名になる col_level:meltする変数(カラム)のレベル指定
data_long[‘post’] = (data_long[‘time’] == ‘post_treatment’).astype(int)
最後に処置を受けたかどうかの列を生成してデータフレームの完成です。
一番重要なのは、モデルの部分ですね。交互作用項を使って差の差分析をしております。
線形回帰モデル(model = smf.ols(‘outcome ~ treated * post’, data=data_long))を適用しています。
このモデルは、処置群、対照群、処置前、処置後のすべての組み合わせを考慮した交互作用項(treated * post)を含むことで、差の差分析を実行しています。
$$Y_{it}=β_{0}+β_{1}×Treated_{i}+β_{2}×Post_{t}+β_{3}×(Treated_{i}×Post_{t})$$
交互作用項を利用する理由は、処置群と対照群の処置前と処置後のアウトカムの差を、それぞれの組み合わせに対して別々に評価できるためです。
これにより、処置群と対照群の処置前のアウトカムの差によるバイアスが取り除かれ、処置の効果をより正確に推定できます。
平均処置効果は4.93でした!
post_treatment = pre_treatment + np.where(treated, 5, 0) + np.random.normal(0, 2, size=n)で元々5の効果があると仮定しているので当たり前ですが、うまく効果が導けました。
OLS Regression Results
==============================================================================
Dep. Variable: outcome R-squared: 0.044
Model: OLS Adj. R-squared: 0.042
Method: Least Squares F-statistic: 30.32
Date: Mon, 08 May 2023 Prob (F-statistic): 3.62e-19
Time: 00:23:17 Log-Likelihood: -7456.5
No. Observations: 2000 AIC: 1.492e+04
Df Residuals: 1996 BIC: 1.494e+04
Df Model: 3
Covariance Type: nonrobust
================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------
Intercept 50.4618 0.455 110.844 0.000 49.569 51.355
treated -0.1179 0.637 -0.185 0.853 -1.368 1.132
post 0.1115 0.644 0.173 0.863 -1.151 1.374
treated:post 4.9302 0.902 5.469 0.000 3.162 6.698
==============================================================================
Omnibus: 1.288 Durbin-Watson: 2.033
Prob(Omnibus): 0.525 Jarque-Bera (JB): 1.313
Skew: 0.026 Prob(JB): 0.519
Kurtosis: 2.886 Cond. No. 6.92
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Average Treatment Effect: 4.93
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!






