成田悠輔教授の論文でも使われた回帰不連続デザイン(RDD)を学ぶ|python
今回は、子供に対する教育機関の因果効果を分析した、成田悠輔教授の論文を通して、回帰不連続デザインを解説いたします。
参照文献:Regression Discontinuity in Serial Dictatorship:Achievement Effects at Chicago's Exam Schools ByATLA ABDULKADIROGLU, JOSHUA D.ANGRIST, YUSUKE NARITA, PARAG A.PATHAK, AND ROMAN A.ZARATE American Economic Review:Papers&Proceeding 2017 ,107(5):240-245
回帰不連続デザイン(regression discontinuity design)
まずは回帰不連続デザインについて簡単に見ていきましょう。
-どんな時に使うか-
回帰不連続デザインは、決定的な割り当てがあるときに使います。
決定的な割り当てがある場合、セレクションバイアスが生じている恐れがあり、データ全体で回帰を行うと誤った解釈を招く恐れがあります。
セレクションバイアスとは、介入以外の属性の差によるバイアスです。
例えば、進学校には学力を伸ばす機能があるかどうか調べたときに、進学校に合格できた場合の集合と、不合格だった場合の集合でナイーブな比較をします。
このときは、「進学校による教育効果」の他にも、「もともとの学力や才能が高かったから進学校にも合格できたし、その後の学力も高かった」と言えてしまいます。
これをセレクションバイアスと呼び、介入をするかどうかをある閾値によって明確に分ける場合に発生します。
例1:1,500g未満の未熟児はNICUに入れる。1,500g以上の新生児は入れない。
例2:動画を 一日3時間未満見る人には広告を見せない/3時間以上なら広告を見せる
など、例を挙げるとキリがありません。
*NICU(Neonatal Intensive Care Unit)とは新生児集中治療室のこと。
明確な因果効果を見たいときは、介入/非介入を無作為に割り付けることが必要です。
しかし、主に社会科学の分野においては、倫理的/金銭的/ビジネスの観点からターゲットをあらかじめ絞って介入が行われます。
このような場合に、回帰不連続デザインは使われます。
-回帰不連続デザインで行うこと-
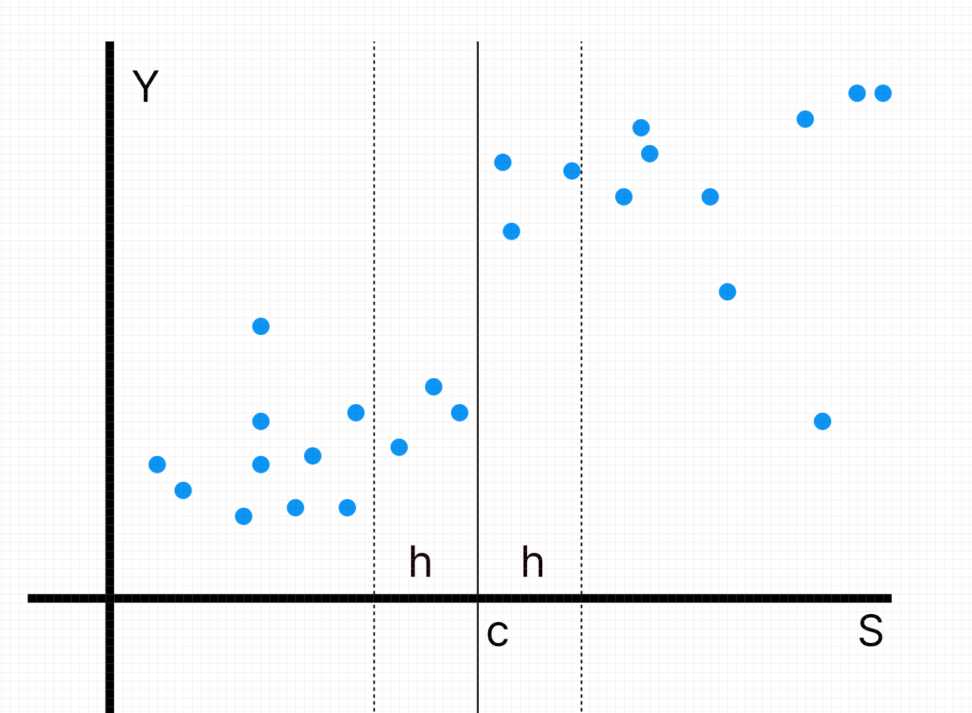
回帰不連続デザインでは、閾値(cutoff)付近のデータだけに注目し、回帰分析を行います。
手順としては、
①介入群の回帰を行う
②コントロール群の回帰を行う
③結果を比較する。期待値の差を取るなど。
c:カットオフ。介入と非介入を分ける閾値です。
running variable:ランニング変数、強制変数。介入と非介入の軸であり、テストの点などが挙げられます。\(S_{i}\)は個人iのランニング変数です。
Y:結果変数。\(Y_{1i}\)は介入を受けた個人iの結果変数を表し、\(Y_{0i}\)は介入を受けていない個人iの結果変数を表します。
h:バンド幅。「近傍」を設定するための範囲です。
D:介入を受けたかどうかを示すダミー変数。介入を受ければ1、受けなければ0を取ります(完全遵守)。
Dに関してですが、未熟児の例のような「割り付けが純粋に受け入れられる」場合は、「完全遵守」となります。
一方、「不合格だったが裏口入学をして合格した」「合格したけど別の学校に行った」などの天邪鬼がいる場合には、不完全遵守と呼ばれ、シャープな回帰不連続デザインではなくなります。
この時の問題設定は、ファジーな回帰不連続デザインと呼ばれ、操作変数法が使われたりします。
今回は、シャープな場合に説明を限定しています。
$$Y_{it}=β_{0}+β_{1}D_{1}+β_{2}(S_{i}-c)+β_{3}D_{i}(S_{i}-c),c-h<S_{i}<c+h$$
第4項は交互作用項です。
回帰不連続デザインによって求められた因果効果をLATE()と呼びます。
局所的な平均処置効果は、以下のとおりです。
$$τLATE = \displaystyle\lim_{x↓c}E[Y|X=x]-\displaystyle\lim_{x↑c}E[Y|X=x]$$
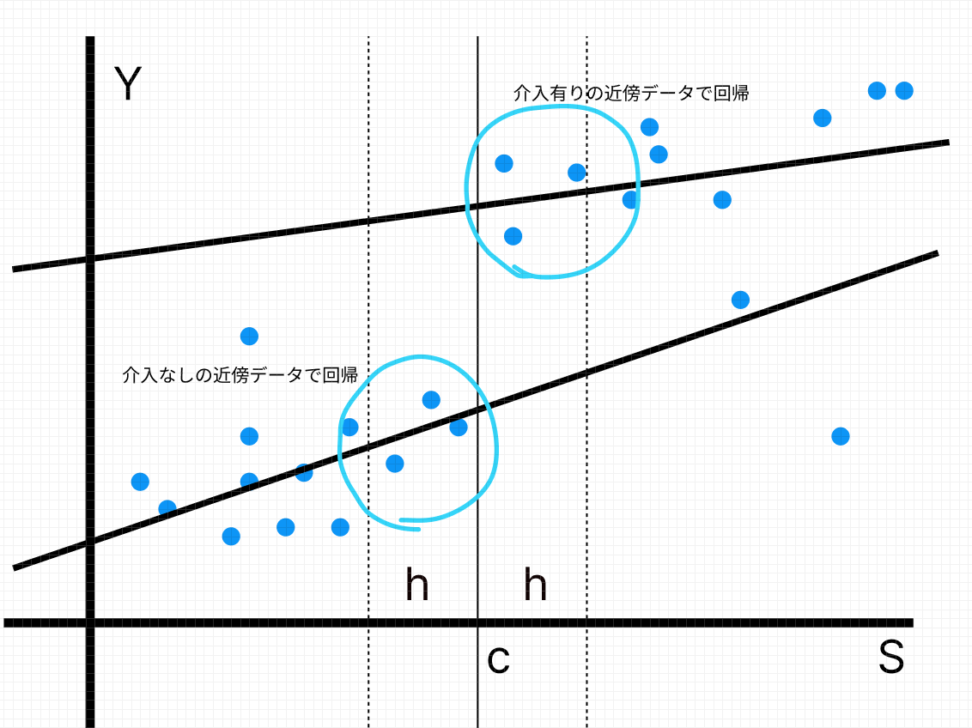
上のように、介入ありの近傍データと介入なしの近傍データで回帰を行います。
そして横軸のcにおけるYの値の差が、局所的な平均処置効果にあたります。
平均処置効果の基本については、以下をご覧ください。
【共変量の調整】傾向スコア・マッチングによる因果推論 | python
【A/Bテストなし】競合施策の効果を推定したい|因果推論と時系列解析
running valuables(ランニング変数)におけるc(閾値)付近では、誤差の範囲内で割り付け確率がブレるという解釈ができます。
先ほどの例というと、合格最低点のA君と惜しくも1点届かなったB君の共変量は、ほとんど確からしいといえます。
このカットオフ付近のデータであれば、セレクションバイアスがないという観点から、擬似的な無作為の割り付けができるというわけです。
Rubinの因果推論の定義に従って言い換えると、カットオフの近傍であれば、\(E[Y_{1i}|S_{i}]\)と\(E[Y_{0i}|S_{i}]\)が連続であるということです。
「潜在的結果変数(Y0,Y1)の条件付き分布には連続性がある」という、いわばこの連続性の仮定が満たされない限り、回帰不連続デザインによる局所的な平均処置効果の推定はできません。
バンド幅はどのように決定するのか
バンド幅が狭いと、セレクションバイアスが小さくなる一方で、そもそも参照するデータが少なくなります。
こうした論点から、バランスしたバンド幅を決定させるにはどうすれば良いのでしょうか。
これについては、明確な結論が出ておらず、現在も理論計量経済学者の間でも議論が続いています。
今のところはhの範囲を設定し、推定結果を都度確認して、頑健なhを探索する方法が良いでしょう。
論文解説:学校による教育効果はあるのか
ここからは、成田教授の論文の概要と回帰不連続デザインがどのような使われ方をしたかどうかを簡単に見ていきます。
回帰不連続デザイン以外の推定方法などは触れませんのでご留意ください。
-目的-
特定の学校による教育効果ではなく、学校セクター全体の教育効果を考えています。
中でもシカゴの受験校が生徒の学力に及ぼす影響を推定します。
-背景-
日本とは異なる受験システムになっているので少し背景を説明します。
シカゴの学生は8年生の時に、入学する学校を選択するそうです。
9年生から入学したい学校を9校の中から最大6位までランクづけして、入学を希望します。
受験校は、入学試験、GPA、7年生の標準化されたテストの得点から作られる共通の複合指標を用いて、受験者を選びます。
この複合指数が実行変数(running valuables)です。
また、学校の割り当ての仕組みに関しては、アファーマティブアクションとして、各家庭の社会経済状況を考慮していますが、詳しくは論文をご覧ください。
実際の教育効果を見るための指標としては、10年生のPLANテストと11年生のACTテストで測定される学力を採用しています。
θ:希望する学校のランクづけのパターン i:個人 s:学校 c:カットオフ値 D_is:個人iに学校sが割り当てられかどうかに関するダミー変数
serial dictatorshipとは
この論文で出てくるserial dictatorship(SD)とは、誰から順に好きなものをとらせてあげるかという問題で、
今回の試験のようなSDでは、実行変数となる複合指標が高い人から順番に学校が割り当てられるということになります。
random serial dictatorshipなら、例えばくじ引きでお菓子を先に選ぶ人を決められる、みたいなルールになります。
-手法-
成田悠輔教授の論文では、回帰不連続デザインと傾向スコアを組み合わせた手法を使っています。
また、二段階最小二乗法と操作変数法を使って推定を行なっております。
傾向スコアに関しては、条件付き割り付け確率を求めます。
$$p_{s}(θ)=E[D_{is}|θ_{i}=θ]$$
傾向スコアについては、青の統計学でも解説しております。以下のコンテンツをご覧くださいませ。
【共変量の調整】傾向スコア・マッチングによる因果推論 | python
-回帰不連続デザインの使われ方-
論文では、局所的な割り付け確率をバンド幅δを使って以下のように出しています。
r0をカットオフ値とすると、
$$q_{s}(θ;r_{0},δ)=E[D_{i}|θ_{i}=θ,R_{i}(\in{(r_{0}-δ,r_{0}+δ)})]$$
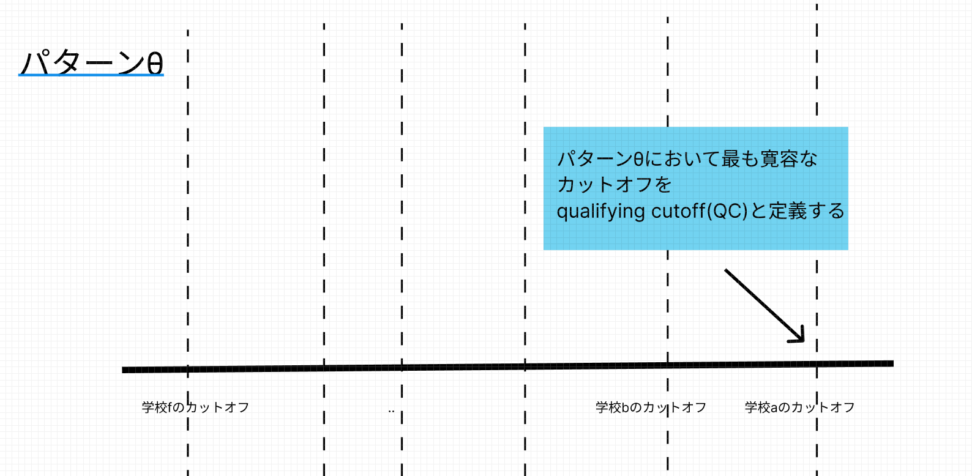
パターンθにおいて最も寛容(入りやすい)カットオフをQCとしています。
そして、局所的な割り付け確率は、以下のように表すことができます。
$$\hat{q}_i = \left\{\array{0&r_{0}>QC_{θ}+δ_{s}\\0.5&r_{0} \in{[QC_{I}-δ_{s},QC_{I}+δ_{s}]} \\1&r_{0}<QC_{θ}-δ_{s}}\right.$$
難しそうですが、単純にどこにも受からなかったら割り付け(自分の優先順位づけした学校に入学する)を受けられないよ、ということです。
一番カットオフが緩いQCを上回れば、何らかの割り付けは受けられるというわけです。
そして、今回割り付けを受けるか受けないかの境界は紛れもなく、最もカットオフ値が緩いQCなので、QC近傍のデータを使います。
論文でも、十分小さいδを選択(つまりバンド幅を狭くする)ことで、OVB(欠落変数バイアス)を実行変数から除き、かつ志願者の選好(おそらく行きたい学校の順位づけパターン)による交絡を排除することができると言及しています。
-結論-
統計的には有意な結果は出ませんでした。
学校に教育効果があるのかどうか、よくわからないという結論です。
経済学では、「人的資本理論」と「シグナリング理論」という対照な理論があります。
人的資本理論は、人に教育やスキルなどが蓄積されていくという理論で、学校教育の話であれば、入学した学校による教育効果で人的資本が増加したと考えます。
一方で、シグナリング理論では、学校に入学できたという事実から、その時点の才能や学力をもって学生を評価すると考えます。
今回の結果は、学校教育による効果に有意性が認められないことから、シグナリングを示唆する内容だと考えます。
まとめ
回帰不連続デザイン(Regression Discontinuity Design, RDD)は、研究において標本を選択するための方法の一つです。
RDDは、特定のしきい値によって、標本が選ばれるかどうかが決まるときに使用されます。
閾値は、変数のスコアやスコアに基づくランクなどが考えられます。
RDDは、研究対象となる治療やプログラムの効果を測定するために使用されることが多いです。
例えば、学校入学に必要なスコアがある場合、スコアがしきい値以上の学生とスコアがしきい値未満の学生を比較し、学校入学が学生の成績に与える影響を調べることができます。RDDは、ランダム化実験に比べて簡単に実施することができ、効果を測定するために有用な情報を提供することができます。
RDDを使用するためには、しきい値周辺において、標本のランダム性が保証されていることが重要です。
これは、しきい値が選ばれるための理由ではなく、ランダムな要因によって選ばれることが重要です。
また、RDDの結果を正しく解釈するためには、評価対象の変数がしきい値以上の場合と未満の場合で、同様に分布していることが重要です。
RDDは、1960年代には確立されていた手法です(1980年代に確立された傾向スコアより前)が、注目する部分を狭くすることによる、
データ量の少なさからくる精度の悪さがネックになっていましたが、自然実験による因果効果の推定に使えることから、注目されてきました。
横軸に時系列を設けるものは、中断時系列デザインと呼ばれ、自己相関を考える必要があります。
RDDでは、基本別の個人(テストの点など)を想定しているため、自己相関などは考えなくても良いです。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


