【統計学】分散不均一だと何が問題なのか|不偏性とガウスマルコフ性について
そもそも、なぜ「分散不均一」が問題なのか?
「分散不均一」とは、我々分析者が日常で直面する様々な現象を回帰等で統計的に捉えようとする際に直面する概念です。
例えば、所得が増えるにつれて支出のばらつきが大きくなる、あるいは学習時間が増えるにつれてテストの点数のばらつきが小さくなる、といった状況ですね。これらはまさに、データの「分散」が一定ではない、つまり分散不均一な状態を示しています。このような状況で、安易に統計モデルを適用してしまうと、思わぬ落とし穴にはまってしまうことがあります。

体験談で言うと、事業会社で店舗ごとの予約数と、店舗ごとのクチコミ数を分析したことがあります。予約数を予測しようとすると、クチコミ数が増えれば増えるほど、予約数のばらつきが大きくなっていきました。典型的な分散不均一ですね。

これはつまり、「クチコミ数は予約数の底上げには繋がるが、上がってからは他の要因が大きく影響してくる」という示唆ですね。
予測タスクをするだけとなると、対数変換等がセオリーですが、「何が要因なのか」のように因果に踏み込む分析要求の方が多いと思います。
分散不均一性(Heteroscedasticity)とは?
数学的背景:誤差項の分散が一定でないということ
回帰分析、特に線形回帰モデルを考える際、私たちは通常、以下のようなモデルを仮定します。
$${ Y_i = \beta_0 + \beta_1 X_i + \epsilon_i }$$
- $Y_i$ は目的変数(被説明変数)
- $X_i$ は説明変数
- $ \beta_0 $ は切片
- $ \beta_1 $ は傾き(回帰係数)
- $ \epsilon_i $ は誤差項(残差)
で、誤差項 $ \epsilon_i $ は、モデルでは説明しきれない部分や、測定誤差など、様々な要因によって生じる「ノイズ」のようなものです。
線形回帰モデルの古典的な仮定の一つに、「誤差項の分散が均一である」というものがあります。これを「等分散性(Homoscedasticity)」と呼びます。数学的に表現すると、以下のようになります。
$${ Var(\epsilon_i) = \sigma^2 }$$
これは、すべての観測値 $i$ において、誤差項 $ \epsilon_i $ の分散が一定の値 $ \sigma^2 $ である、という意味です。

つまり、説明変数 $X_i$ の値が小さくても大きくても、目的変数 $Y_i$ のばらつきの幅は変わらない、ということを意味します。例えば、所得と貯蓄の関係を考えるとき、所得が低い人々の貯蓄のばらつきと、所得が高い人々の貯蓄のばらつきが同じである、と仮定していることになります。
しかし、現実のデータでは、この仮定が成り立たないことがしばしばあります。説明変数 $X_i$ の値が変化するにつれて、誤差項 $ \epsilon_i $ の分散も変化する状況を「分散不均一性(Heteroscedasticity)」と呼びます。
数学的には、以下のように表現されます。
$${ Var(\epsilon_i) = \sigma_i^2 }$$
$ \sigma_i^2 $ は、観測値 $i$ ごとに誤差項の分散が異なることを示しています。つまり、説明変数 $X_i$ の値によって、目的変数 $Y_i$ のばらつきの幅が変わる、ということです。
繰り返しにはなりますが、先ほどの所得と貯蓄の例で言えば、所得が低い人々の貯蓄のばらつきは小さいが、所得が高い人々の貯蓄のばらつきは非常に大きい、といった状況が分散不均一性に該当しますね
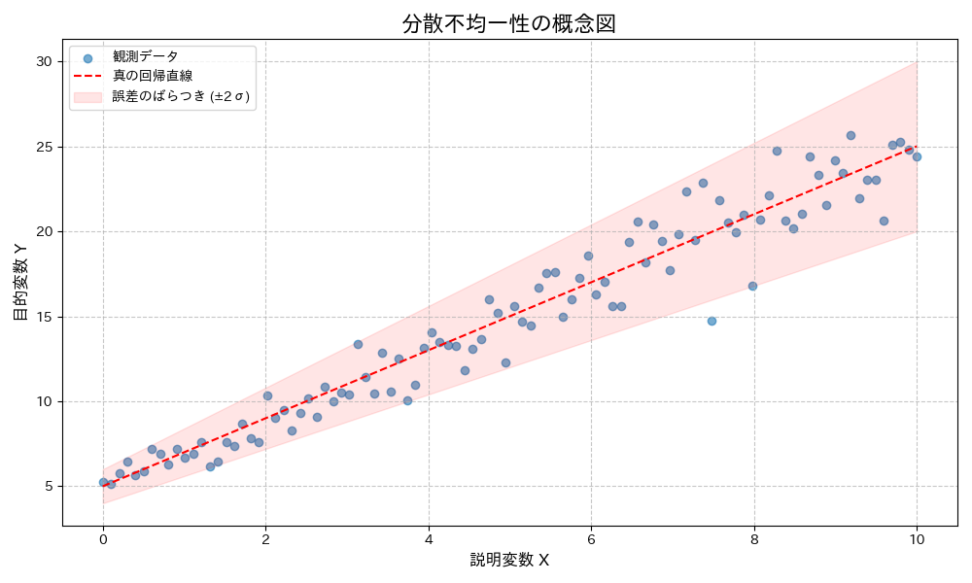
そもそも説明変数ではない誤差項にどんな役割があるのでしょうか。
実は回帰係数の分散を求める際に、誤差項の分散を利用します(例:OLS推定)
$$V[\hat{β_1}|x_1,x_2,…x_n]=\frac{s^2}{\sum_{i=1}^n(x_i-\overline{x})^2}$$
ただし、誤差項の分散sなんて直接求めることはできません。
分散均一の場合、以下のように誤差項の分散は表すことができます。
$$\hat{s}=\frac{1}{n-2}\sum_{i=1}^{n}\hat{u}_{i}^2$$

分散を直接求めることはできないので残差(予測値と実際の観測データの差)を使っているということです。
つまり、分散不均一な場合の最小二乗推定量の分散の求め方は以下のようになります。
$$Var(\hat{β}) = \frac{\sum_{i=1}^n(u_{i}^2 * x_{i}^2)} {\sum_{i=1}^{n}(x_i – \overline{x})^2}^2$$
不偏性(Unbiasedness)とは?
では、前提知識を揃えていいきましょう。
しばしば、手元の限られたデータ(標本)から、そのデータが属するより大きな集団(母集団)の特性を推測しようとします。この推測を行う際に用いられるのが推定量です。例えば、母集団の平均(母平均)を推定するために、標本から計算される標本平均などが推定量にあたりますね。
数学的背景:期待値と真の値
良い推定量にはいくつかの望ましい性質がありますが、その中でも特に重要なのが「不偏性(Unbiasedness)」です。不偏性とは、簡単に言えば、「その推定量を何度も繰り返し計算したときに、平均的に真の値と一致する」という性質のことです。
数学的に表現すると、ある母数 $ \theta $ の推定量 $ \hat{\theta} $ が不偏であるとは、その期待値が母数 $ \theta $ に等しいことを意味します。
$${ E[\hat{\theta}] = \theta }$$
$ E[\hat{\theta}] $ は推定量 $ \hat{\theta} $ の期待値を表します。
期待値とは、確率変数がとりうる値にその確率を掛け合わせたものの合計であり、簡単に言えば「平均的にどのような値をとるか」を示すものです。つまり、不偏性がある推定量は、たとえ個々の推定値が真の値からずれたとしても、長期的に見ればその「ずれ」が相殺され、平均的には真の値にたどり着く、ということを保証してくれるのです。
詳しくは、以下の記事をご覧ください。
例えば、母平均 $ \mu $ を推定する際に、標本平均 $ \bar{X} $ を用いることを考えます。
標本平均は、不偏推定量であることが知られています。これは、どんな母集団から標本を抽出しても、標本平均の期待値が母平均に等しい、つまり $ E[\bar{X}] = \mu $ が成り立つことを意味します。結構当たり前に使っていますが、だからこそ、標本平均を母平均の「良い」推定量として信頼して使うことができているのです。
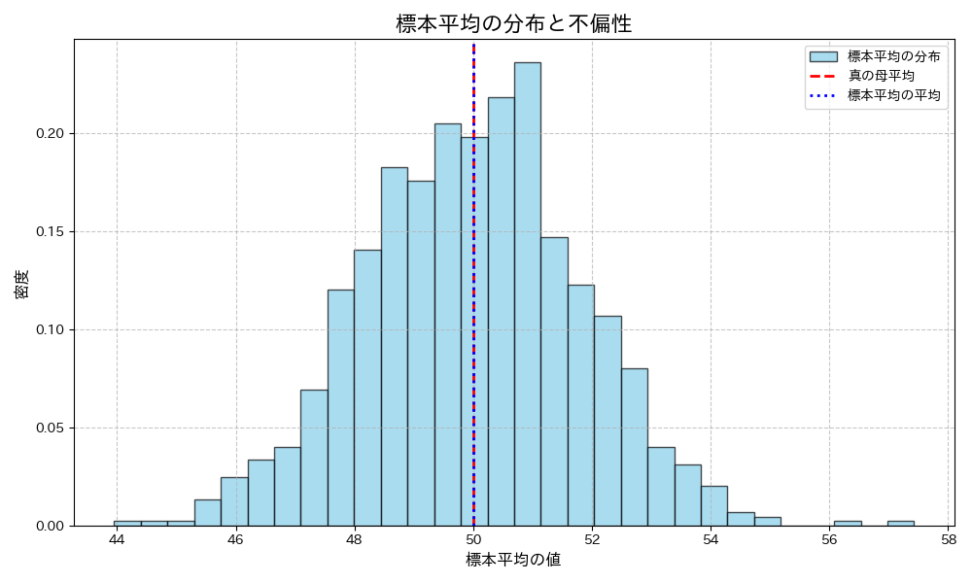
推定量の「偏り」とは何か
当然ですが、推定量 $ \hat{\theta} $ に偏りがある場合、その期待値は真の値 $ \theta $ と一致しません。
$${ Bias(\hat{\theta}) = E[\hat{\theta}] – \theta \neq 0 }$$
この偏りを、バイアスと呼びます。
例えば、標本分散を計算する際に、単純に各データと標本平均との差の二乗を合計して標本サイズ $n$ で割った場合、その推定量は母分散を過小評価する傾向があることが知られています。そのため、不偏な推定量を得るためには、$n$ ではなく $n-1$ で割る「不偏分散」を用いるのが一般的です。
詳しくは、上で紹介した記事に記載しておりますが、 $n-1$ は「自由度」と呼ばれ、不偏性を確保するための役割を果たします。
ここまで、不偏性は推定量の「正確さ」を保証する性質とということがわかりました。ただ、不偏性だけでは十分ではありません。推定量がどれだけ「ばらつき」が少ないか、つまり「効率性」もだいじな性質です。次のセクションでは、この不偏性と効率性を結びつける定理である「ガウス・マルコフの定理」について解説します。
ガウス・マルコフの定理とOLS推定量の「最良」性
線形回帰モデルにおいて、一般的に用いられる推定方法は「最小二乗法(Ordinary Least Squares; OLS)」です。OLSは、実際の観測値と回帰直線によって予測される値との残差(誤差)の二乗和が最小になるように回帰係数を推定する手法です。
$$β = (X’X)^{-1}X’y$$
このOLS推定量が、特定の条件下で非常に望ましい性質を持つことを保証するのが、「ガウス・マルコフの定理」です。
ガウス・マルコフの定理は、OLS推定量が「最良線形不偏推定量(Best Linear Unbiased Estimator; BLUE)」であることを主張します。しかし、この定理が成り立つためには、いくつかの前提条件が必要です。
ガウス・マルコフの定理の前提条件
1. 線形性 (Linearity): モデルがパラメータに対して線形であること。つまり、$Y_i = \beta_0 + \beta_1 X_i + \epsilon_i$ のように、回帰係数 $ \beta_0, \beta_1 $ が線形の関係で表現されていること。
2. 誤差項の期待値がゼロ (Zero Conditional Mean): 誤差項の期待値がゼロであること。$E[\epsilon_i | X_i] = 0$。これは、説明変数 $X_i$ の値に関わらず、誤差項の平均が常にゼロであることを意味します。つまり、モデルが説明変数によって捉えきれない部分に、系統的な偏りがないことを示します。
3. 誤差項の等分散性 (Homoscedasticity): 誤差項の分散が一定であること。$Var(\epsilon_i | X_i) = \sigma^2$。これは、セクション1で詳しく説明した「分散均一性」の仮定です。説明変数 $X_i$ の値に関わらず、誤差項のばらつきの大きさが常に同じであることを意味します。
4. 誤差項の無相関 (No Autocorrelation): 異なる観測値の誤差項が互いに無相関であること。$Cov(\epsilon_i, \epsilon_j | X_i, X_j) = 0$ for $i \neq j$。これは、ある観測値の誤差が、他の観測値の誤差に影響を与えないことを意味します。時系列データなどでは、この仮定が破られることがあります。
5. 説明変数の外生性 (Exogeneity of Explanatory Variables): 説明変数 $X_i$ が確率的である場合、誤差項と無相関であること。$Cov(X_i, \epsilon_i) = 0$。これは、説明変数が誤差項に影響を与えない、あるいは誤差項が説明変数に影響を与えない、という因果関係の方向性を示唆します。
もし満たされない場合、OLS推定量の望ましい性質が失われる可能性がありますが、まあ現実的には難しかったりします。
これらの仮定のうち、今回トピックに挙げているのが「誤差項の等分散性」です。ガウス・マルコフの定理は、この等分散性の仮定が満たされている場合に、OLS推定量の「最良」性が保証されることを示しています。
OLS推定量の不偏性
ガウス・マルコフの定理の結論の一つは、上記の仮定(特に線形性、誤差項の期待値がゼロ、説明変数の外生性)が満たされていれば、OLS推定量は不偏である、ということです。つまり、OLSによって推定された回帰係数 $ \hat{\beta}_0, \hat{\beta}_1 $ の期待値は、母集団の真の回帰係数 $ \beta_0, \beta_1 $ に等しくなります。
$${ E[\hat{\beta}_0] = \beta_0 }$$
$${ E[\hat{\beta}_1] = \beta_1 }$$

これは嬉しいですね。OLS推定量が平均的に真の値を正確に捉えることができるということです。
OLS推定量の効率性:BLUEとは何か
ガウス・マルコフの定理のもう一つの結論は、OLS推定量が「最良」である、という点です。ここでいう「最良」とは、線形不偏推定量の中で、最も分散が小さい、という意味です。つまり、OLS推定量は、他のどんな線形不偏推定量と比較しても、推定値のばらつきが最も小さい、ということです。
この性質を持つ推定量を「最良線形不偏推定量(BLUE)」と呼びます。分散が小さいということは、推定値が真の値の周りに密集していることを意味し、より「精密」な推定が可能である、と言い換えることができます。不偏性が「正確さ」を保証するのに対し、効率性(分散が小さいこと)はいわゆる「精密さ」を保証する性質です。
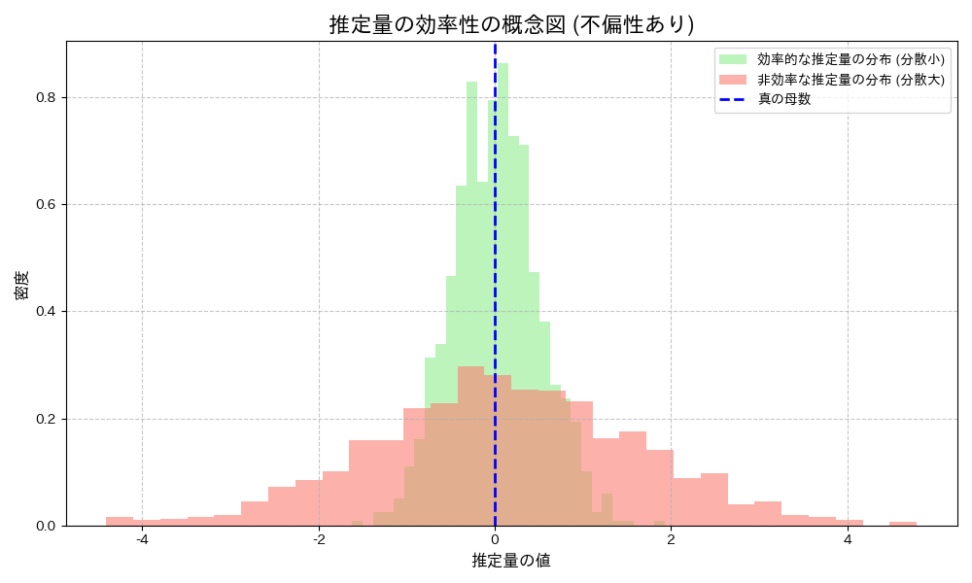
↑こんな感じに、どちらも分布の真ん中が確かに真の母数と一致していそうですが、赤い分布はばらつきが多く、推定量が母数と近くなるのか怪しいですね。
そもそも、私たちが限られたデータから母集団の特性を推測する際に、できるだけ信頼性の高い、つまり「正確で精密な」推定値を得たいので、不編性はもちろんのこと、推定量が効率的であればあるほど嬉しいですよね。
OLS推定量は、ガウス・マルコフの定理の仮定が満たされていれば、この両方の性質を兼ね備えているため、線形回帰分析において「まずはこれをやっておくか」となるのです。
以下のコンテンツでは、推定量の分散の下限を設定できる「クラメールラオの下限」について言及しています。
【統計検定】フィッシャー情報量とクラメール・ラオの不等式について解説|python
本題。分散不均一性がOLS推定に与える影響
では、もしガウス・マルコフの定理の仮定の一つである「等分散性」が満たされず、分散不均一性が存在する場合、OLS推定量はどのような影響を受けるのでしょうか。
不偏性は保たれるが、効率性が失われる
分散不均一性が存在しても、OLS推定量は不偏性を保ちます。つまり、誤差項の分散が一定でなくても、OLSによって推定された回帰係数の期待値は、依然として母集団の真の回帰係数に等しいということです。
しかし、問題は効率性にあります。分散不均一性が存在すると、OLS推定量は「最良線形不偏推定量」ではなくなります。つまり、他の線形不偏推定量と比較して、OLS推定量の分散が最小ではなくなってしまうのです。
ではなぜか。
分散不均一性がある場合、各観測値の誤差のばらつきが異なります。OLSは、これらの異なるばらつきを均等に扱ってしまいます。
- 誤差の分散が大きい観測値
- データに大きな「ノイズ」が含まれていることになります。OLSは、これらのノイズの多いデータ点を、ノイズの少ないデータ点と同じ重みで扱ってしまう。
- 誤差の分散が小さい観測値
- データに信頼性が高いことになります。OLSは、これらの信頼性の高いデータ点の情報を、十分に活用できていないイメージ。
標準誤差の過小評価と仮説検定の信頼性
分散不均一性がOLS推定に与えるもう一つの影響一つは、回帰係数の標準誤差が正しく推定されなくなることです。具体的には、多くの場合、標準誤差が過小評価される傾向にあります。標準誤差は、推定量のばらつきの程度を示す指標であり、推定量の信頼性を測る上での指標です。
詳しくはこちら。
つまり、分散不均一性がある状況でOLSをそのまま適用すると、推定された係数自体は不偏であっても、その係数がどれくらい信頼できるか(ばらつきが小さいか)という情報が歪んでしまい、統計的推論の根幹である仮説検定の信頼性が損なわれるのです。
おまけ|分散不均一性への対処法
分散不均一性がOLS推定に与える影響を理解した上で、では実際にそのような状況に直面した場合、どのように対処すれば良いのでしょうか。ここでは、主な対処法を紹介します。
ホワイトの標準誤差
最も一般的に用いられる対処法の一つが、「頑健な標準誤差(Robust Standard Errors)」、または「ロバスト標準誤差」を用いる方法です。この方法は、OLS推定量の不偏性は保たれるという性質を利用し、標準誤差の計算方法を修正することで、分散不均一性があっても信頼できる仮説検定や信頼区間を構築できるようにします。
具体的には、誤差項の分散が不均一であることを考慮した上で、標準誤差を推定し直します。
分散不均一に対して頑健な標準誤差の一つとして、ホワイトの標準誤差というものがあります。
手順を示します。Xは説明変数を格納した行列です。
- OLS(Ordinary Least Squares)によってパラメータを推定し、残差 \(\hat{ε}\) を計算します。
- ホワイトの標準誤差は線形回帰で使用可能です。
- 残差 \(\hat{ε}\) の二乗と説明変数 X の外積の行列を計算します。
- これらの行列の和を計算し、それを S とします。
- $S = \sum \hat{ε}_i^2 * (X_i X^T_i)]$
- この外積和を使って分散不均一に頑健な共分散行列を計算します。
- $V(\hat{β}) = (X^TX)^{-1} * S * (X^TX)^{-1}$
- ホワイトの頑健な標準誤差は、この共分散行列 \(V(\hat{β})\) の対角要素の平方根として計算されます
- $\pmatrix{ V(X_1)&COV(X_1,X_2)&…&COV(X_1,X_n) \\ COV(X_2,X_1)&V(X_2)&…&COV(X_n,X_1) \\ COV(X_n,X_1)&COV(X_n,X_2)&…&V(X_n)}$
対角要素なので、ただの分散ですね
例えば、共分散行列\(V(\hat{β})\) のある対角要素を\(v_{ii}\)とすると
$$SE(\hat{β}_i) = \sqrt{v_{ii}}$$
では、共分散行列を使うことで頑健になるのでしょうか?
対角行列つまり分散の平方根(つまり標準偏差)は、値のばらつきの度合いを表す統計的な尺度であり、元のデータの単位と同じ単位で解釈できるのが特徴です。
よって共分散行列の対角要素の平方根を取ることで、各パラメータの推定値のばらつきの度合い(つまり不確実性)を直感的に解釈可能な形で表現することができます。
これにより、係数推定値自体はOLSによるものと同じですが、その信頼性を示す標準誤差がより正確なものになります。結果として、t値やp値も適切に計算され、仮説検定の信頼性が回復します。
この方法は、OLS推定量の不偏性を維持しつつ、分散不均一性の問題を比較的容易に解決できるため、実務で広く利用されています
おまけ|ブルーシュ=ペーガン検定とホワイト検定
これまで分散不均一の問題点や特徴を解説してきましたが、最後に分散不均一かどうかを判定することが重要でしょう。
ここでは、ブルーシュ-ペーガン検定とホワイト検定について解説します。
ブルーシュ=ペイガン検定
回帰分析の残差の二乗を従属変数とする新たな回帰モデルを設定します。
$$Y = Xβ + ε$$
$$ε^2 = Zγ + u$$
元の回帰式の誤差項の二乗が目的変数になっていますね。
Zは通常Xと同じ説明変数を格納した行列ですが、説明変数が誤差項のうちどのくらいを説明できるかを考えます。
次に、\(ε^2 = Zγ + u\)の決定係数を使って、LM統計量(Lagrange Multiplier Statistics)を\(nR^2\)を計算し、カイ二乗分布を用いてp値を計算します。
帰無仮説が棄却されると分散不均一と言えます。
→棄却できないことが望ましい。
ホワイト検定
誤差の分散が説明変数の非線形関数として表現されるようになっております。
具体的には、回帰分析の残差の二乗を従属変数とする新たな回帰モデルを設定しますが、このとき説明変数(Z*)としては、元の説明変数、その二乗項、および交互作用項を含むことが一般的です。
$$ε^2 = Z*δ + v$$
ここがブルーシュ ペーガンの検定との違いですね。表現力が増しました。
次に、この新たな回帰モデルのF統計量(または\(χ^2\)統計量)を計算し、帰無仮説(誤差の分散が一定である)を検証します。
帰無仮説が棄却されると、分散不均一の存在が示唆されます。
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.stats.diagnostic import het_white
np.random.seed(42) # 乱数のシードを設定して再現性を保証します
# データを生成
n = 100
x1 = np.random.randn(n)
x2 = np.random.randn(n)
error_variance = np.exp(x1)
error = np.random.randn(n) * np.sqrt(error_variance)
y = 3 + 2 * x1 + 0.5 * x2 + error
data = pd.DataFrame({"y": y, "x1": x1, "x2": x2})
# 元の回帰モデルを推定
X = sm.add_constant(data[["x1", "x2"]])
model = sm.OLS(y, X).fit()
# ホワイト検定を実行
white_test_stat, white_test_p_value, _, _ = het_white(model.resid, model.model.exog)
print("White test statistic:", white_test_stat)
print("White test p-value:", white_test_p_value)
ホワイト検定を実装するコードを紹介します。
White test statistic: 21.12266604682107 White test p-value: 0.0007679500542173898
p_valueは相当小さくなりましたね。
つまり、設定した回帰式から生まれた推定パラメータの分散は、まだまだ小さくできる余地があるということです。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!






