【Box-Cox変換】様々な非線形変換について|python
今回は、モデル選択やパラメータチューニングの前に行う、特徴量エンジニアリングについて解説いたします。
中でも、非線形変換は特徴量の偏った分布を正規分布に近づけたりすることができ、高い精度につながることが多いです。
変数変換で使う行列式、ヤコビアンについては以下のコンテンツをご覧ください。
【数理統計学】ヤコビアンをわかりやすく解説|MCMCでの使用例
非線形変換(non liner transformation)
モデルの中でも、非決定木系のモデル(線形回帰モデルなど)は、特徴量の非線形変換により精度が向上しやすいです。
-なぜ精度が向上するのか-
なぜ、外れ値がある・分布が偏っている特徴量を非線形変換をすると精度が上がりやすいのかというと、
回帰分析や統計的検定は背後に正規分布を前提としているからです。
例えば、「重回帰分析の最小2乗推定量(least squares estimator)の分散は、同時に分散も最小である」ということには、正規性が前提とされています。
$${\hat{β}}{\in{argmin}||Y-βX||^2},COV[{\hat{β}}]=σ^2(X^TX)-1≦COV[{\tilde{β}}]$$
回帰分析については、こちらをご覧ください。
対数変換を行うと、正規分布にデータが近づきます。
また、トレンドは消えないものの分散が一様化します。
下のグラフを見てください。
対数変換をした後の移動平均標準偏差は、変換前よりも一様化していることがわかります。
一方で左下のようにトレンドは消えてないですね。
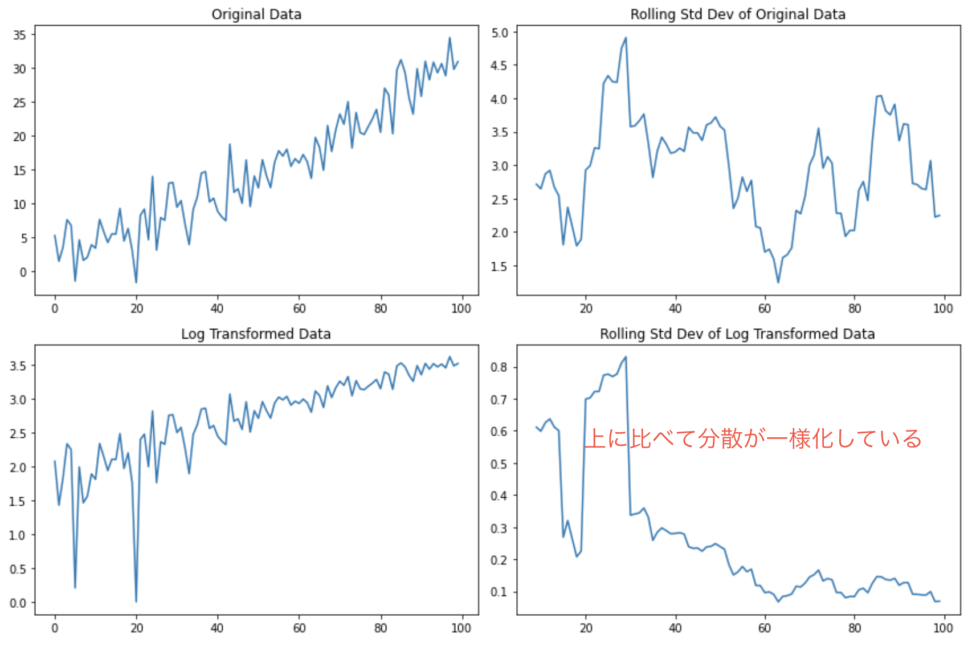
では、分散が一様だと何が嬉しいのでしょうか?
それは、多くの統計的手法が「等分散性」(すなわち、観測値全体で分散が一定であること)を仮定しているからです。 この仮定を満たすことにより、統計的分析の結果が信頼できるものになります。 例えば、線形回帰やANOVA(分散分析)などの手法は、誤差項が等分散性を持つという仮定に基づいています。 これらの手法を使う際には、対数変換や他の適切な変換を用いて等分散性を確保することが重要となります。
非線形変換とは、対数変換や平方変換などが挙げられますが、今回は対数変換を中心に扱っていきます。
対数変換(logarithmic transformation)とBox-Cox変換
対数変換は、Box-Cox変換(ボックスコックス変換)のλ=0の場合を指します。
以下の数式を見てください。
$$x^λ=\left\{\array{{\frac{x^λ-1}{λ}}&λ≠0\\logx&λ=0}\right.$$
Box変換は、特徴量に負の数がある場合は適用はできません。
このような場合には、最小値に+1をしてデータ全体を正の方向に移動してから対数を取る必要があります。
さて、ボックス=コックス変換に必要なλの設定に関しては、AICなどの情報量基準によって正規分布との乖離度を測り、最適な変数変換を行います。
λによっては様々な冪乗変換ができ、いかに変換後のデータの分布が正規分布に近づけられるかを目指します。
CODE
今回は、ボストン住宅価格のデータセットを使ってみます。
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import xgboost as xgb
boston = load_boston()
# Pandasによるデータの表示
df_target = pd.DataFrame(boston["target"], columns=["target"])
df_data = pd.DataFrame(boston["data"], columns=boston["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
df.head()| target | CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | |
| 0 | 24.0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 |
| 1 | 21.6 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 |
| 2 | 34.7 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 |
| 3 | 33.4 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 |
| 4 | 36.2 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 |
さて、特徴量変換の前に実際に分布を見てみます。
特徴量の分布の見方については、以下のコードを参考にしてください。
-単にある一つの特徴量の分布を見たい時-
df.hist(figsize=(20,16))大変便利なメソッドがあります。figsizeでは、出力した図の大きさと縦横比を決定できます。
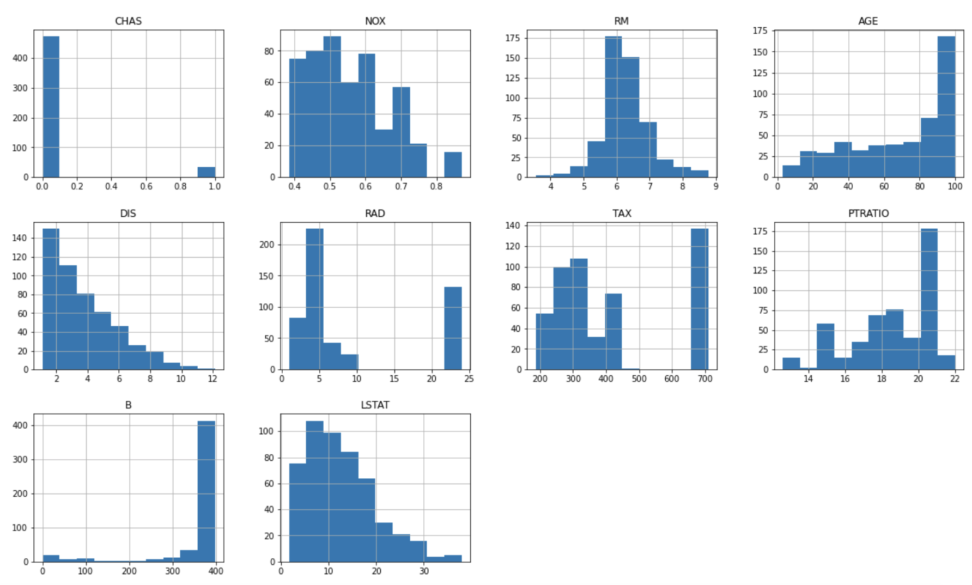
2値分類であるCHAS(チャールズ川沿いかどうか)はともかく、ほとんどのデータが正規分布とは程遠いことがわかります。
-目的変数に対して、ある一つの特徴量の分布を見たい時-
今回の目的変数である、ボストンの住宅価格に紐づけて特徴量の分布を見たい時は、以下のコードを参考にしてください。
import seaborn as sns
sns.jointplot(x="LSTAT",y="target", data=df)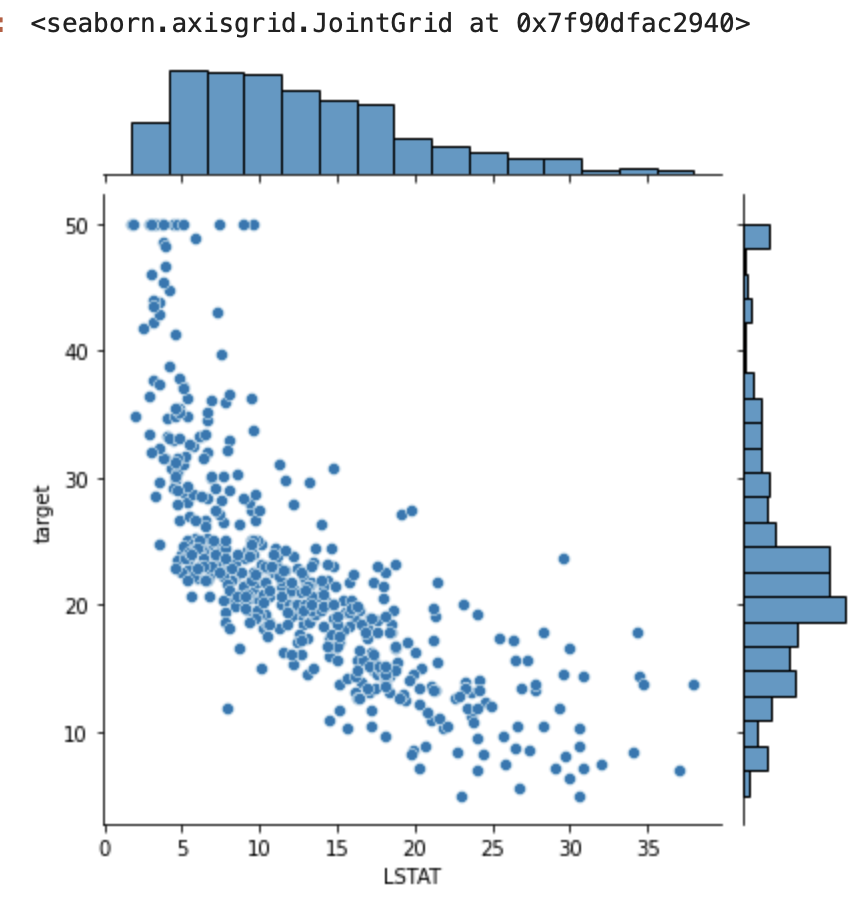
LSTAT(低所得者の割合)を例として分布を出してみました。
低所得者の割合が低い時に、住宅価格は高くなるという傾向が見られますね。
y = df.loc[:,["target"]]
X = df.loc[:, "CRIM":]
# 訓練データとテストデータに分ける
X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.5, random_state=0)
num_cols = list(X.columns)
pos_cols = [c for c in num_cols if (X_train[c]> 0.0).all() and (X_valid[c] > 0.0).all()]
from sklearn.preprocessing import PowerTransformer
pt = PowerTransformer(method="box-cox")
pt.fit(X_train[pos_cols])
#変換後のデータで各特徴量を置き換える
X_train[pos_cols] = pt.transform(X_train[pos_cols])
X_valid[pos_cols] = pt.transform(X_valid[pos_cols])一旦目的変数と説明変数に分け、教師データと評価データに分割します。
上はBox-Cox変換のコードです。λは最適な値に自動で決定されます。
まず、num_colsに説明変数の名前をリスト型で格納しておきます。
次に、for文とif文を使い、値が非負である説明変数のみをpos_colsに格納します。
そしてPowerTransformerというメソッドの引数にbox-coxと指定して、pos_colsのデータをfitさせます。
最後にfitして変換したデータを元のデータと置き換えて出来上がります。
変換後のデータの分布を見てみましょう。
X_train.hist(figsize=(20,16))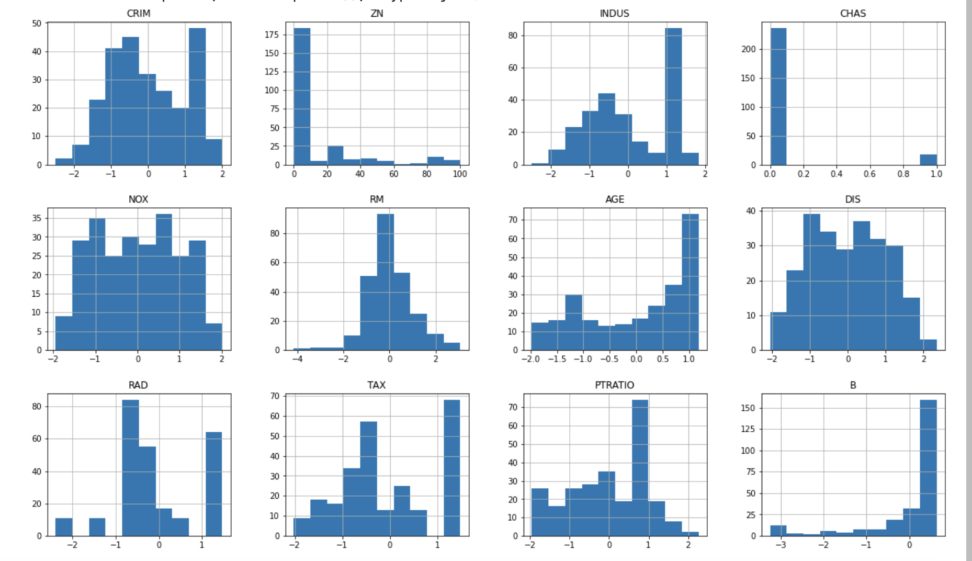
特にCRIMS(犯罪発生率)やNOX(窒素酸化物の濃度)については、正規分布に近づきました。
最後にリッジ回帰にかけてみます。
リッジ回帰については、以下をご覧くださいませ。
【python】Ridge(リッジ)回帰で多重共線性を解決する話
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train,y_train)
y_train_pred = ridge.predict(X_train)
y_valid_pred = ridge.predict(X_valid)
def get_eval_score(y_true,y_pred):
from sklearn.metrics import mean_absolute_error,mean_squared_error,r2_score
mae = mean_absolute_error(y_true,y_pred)
mse = mean_squared_error(y_true,y_pred)
rmse = np.sqrt(mse)
r2score = r2_score(y_true,y_pred)
print(f" MAE(平均絶対誤差) = {mae}")
print(f" MSE(平均二乗誤差) = {mse}")
print(f" RMSE(平均平方二乗誤差) = {rmse}")
print(f" R2Score(決定係数) = {r2score}")
print("教師データスコア")
get_eval_score(y_train,y_train_pred)
print("テストデータスコア")
get_eval_score(y_valid,y_valid_pred)教師データスコア MAE(平均絶対誤差) = 2.972341126745583 MSE(平均二乗誤差) = 16.316436475271708 RMSE(平均平方二乗誤差) = 4.039360899359168 R2Score(決定係数) = 0.8235888468182255 テストデータスコア MAE(平均絶対誤差) = 3.5131054093670606 MSE(平均二乗誤差) = 22.640345162998738 RMSE(平均平方二乗誤差) = 4.75818717191734 R2Score(決定係数) = 0.7013746630894717
非線形変換すべきかどうかを判断するには、まずデータの分布を見ることが大事です。
丁寧なEDA(explanatory data analysis)を心がけましょう。
他の機械学習コンテンツについては以下をご覧ください。
【Sequential】Kerasを使ったニューラルネットワーク|python
【XGB】交差検証法を使った勾配ブースティング決定木の実装|python
【ランダムフォレスト】ブートストラップ法を決定木に応用|python
【判別問題】サポートベクトルマシン(SVM)の仕組み|python




