【第2弾】統計検定準1級のチートシート｜最短合格への道
こんにちは、青の統計学です。
こちらの記事だけでは、紹介しきれない内容があったため第二弾のチートシートになります。
【最短合格】統計検定準一級のチートシート|難易度や出題範囲について
統計検定2級はこちら→【最短】統計検定2級合格ロードマップとチートシート
青の統計学では、統計検定2級以下から勉強したい方も理解できるコンテンツを多くご用意しています。
統計検定準一級のチートシート|その2
| 基礎統計学 | 記述統計 ,確率と確率分布,推測統計, |
| 多変量解析 | 主成分分析,判別分析,因子分析,クラスタ分析, |
| 時系列解析 | 時系列データの特性,ARMAモデル, |
| 実験計画法 | 一般的な実験の計画と分析,分散分析,因子計画 |
| 生存時間解析 | ハザード関数と生存関数,カプラン-マイヤー推定 ,コックス比例ハザードモデル |
| 線形モデル | 単回帰分析,重回帰分析 ,一般化線形モデル |
| ノンパラメトリック | 順位データの分析,散布図と相関 |
| ベイズ統計 | ベイズの定理,事前分布と事後分布,ベイズ的モデル選択 |
| シミュレーション | モンテカルロ法 ,確率的シミュレーション |
合格する際に使用した本
さて、前回と同じく私が合格する際に使い倒した本を1冊だけ紹介させて下さい。
きっとお役に立てるはずです。
統計検定準1級対応 統計学実践ワークブック
統計検定準一級に合格するなら、まず買って欲しい一冊です。
公式が出している教科書であり、例題も豊富で解説もしっかりしています。
おすすめポイントは、例題の豊富さです。
日本統計学会公式認定 統計検定 準1級 公式問題集を買って問題を解いた方はわかると思うのですが、過去問をちょっと複雑にした問題が出ています。
「多項分布の期待値の差の検定統計量が選択式ではない….」
「有限修正の式ってなんだっけ….」
「ポアソン回帰の左辺ってなんだっけ…」
「ロジスティック回帰における説明変数とオッズ比の関係がわからない…」
というように、実際の過去問だと知らなくても平気だった部分も伏せられて出題されています。
この例題等を解けるようになると、強くなっている証拠です。解説も割と丁寧なので、諦めずに取り組めると思います。
おすすめ：統計検定準1級に挑戦したい方
それでは、チートシートに進みましょう。
多変量解析のチートシート
基礎的な内容はこちらをどうぞ！
重回帰分析における最小二乗推定量について
線形回帰モデル\(\textbf{Y}=\textbf{X} \textbf{β}+ε\)を考える時、最小にしたいのは当然２乗誤差です。
$$J(\textbf{β})=(\textbf{Y}-\textbf{Xβ})^T(\textbf{Y}-\textbf{Xβ})$$
お決まりの1階条件を解きます。
勾配が0になるということですね。
$$\frac{∂ J(\textbf{β})}{∂ \textbf{β}}=-2\textbf{X} (\textbf{Y}-\textbf{Xβ})=0$$
$$\textbf{X} (\textbf{Y}-\textbf{Xβ})=0$$
$$\textbf{X}^T \textbf{Y}=\textbf{X}^T \textbf{X}\textbf{β}$$
今回、説明変数の内積である\(\textbf{X}^T \textbf{X}\)が可逆(正則である)と置いているので、左から\(\textbf{X}^T \textbf{X}\)^{-1}\)をかけられます。
よって、最小二乗推定量\(\textbf{β}=(\textbf{X}^T \textbf{X})^{-1}\textbf{X}^T \textbf{Y}\)が得られます。
ちなみに\(\textbf{X}^T \textbf{X}\)は、説明変数間の関係をキャプチャする情報を持っており、この行列が可逆であることは、説明変数間に完全な共線性（一つの説明変数が他の説明変数の線形結合として表されること）がないことを意味します。
多重共線性については、以下のコンテンツをご覧ください。
【論文解説】多重共線性は回帰分析にどのような影響を与えるのか
2変量正規分布における条件付き期待値について
試験だと、兄弟の身長の期待値の問題やTOEICの点数に関わる問題で現れましたね。
正規分布の線形性の性質から、2変量正規分布の一部分の条件付き分布もまた正規分布であることが知られています。
その性質を利用すると、条件付き期待値は次のように計算できます。
$$E(X|Y=y)=E[X]+(y-E(Y))×\frac{COV(X,Y)}{V(Y)}$$
条件付き分布の平均は、 \(X\) の元の期待値に\(Y\)の偏差をスケーリングしたものを加算することで得られます。
ちなみに分散については、以下のようになります。
$$Var(X|Y=y)=σ_X×(1−ρ)$$
正規分布のモーメント母関数について
モーメント母関数は、確率変数のモーメント（期待値、分散など）を簡単に導出するための数学的なツールです。
こちらのコンテンツでもご紹介しましたが、ある分布に従う確率変数の期待値を求めるときに、モーメント母関数を利用すると便利な時があります。
【期待値の応用】モーメント法とモーメント母関数(積率母関数)について
【統計検定】確率分布のモーメント(積率)母関数完全ガイド|導出チートシート
では、正規分布のモーメント母関数を求めてみましょう。
まず、正規分布の確率密度関数は以下のような形ですよね。
$$X~N(μ,σ^2)$$
$$f(x)=\frac{1}{\sqrt{2πσ^2}}e^{-\frac{(x-μ)^2}{2σ^2}}$$
では、モーメント母関数の定義は以下のようになります。
$$M_X(t)=E[e^{tX}]$$
$$M_X(t)=E[e^{tX}]=\int_{∞}^{∞}e^{tx}f(x)dx$$
モーメント母関数の主な利点は、モーメントを効率的に計算できることです。
特に、モーメント母関数を tに関して微分し、その後\( t=0\)とすると、元の確率変数 Xのモーメントを得られます。
導出は以下のようになります。
$$\begin{align*} M_X(t) &= \int_{-\infty}^{\infty} e^{tx} \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} , dx \ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^{\infty} e^{tx – \frac{(x-\mu)^2}{2\sigma^2}} , dx \end{align*}$$
最終的に、モーメント母関数は次のようになります
$$M_X(t)=e^{μt\frac{1}{2}σ^2t^2}$$
これを使えると、例えば誤差項εの期待値が簡単に求められます。
\(ε~N(0,σ^2)\)とすると、\(μ=0,t=1\)となるので、E(exp(ε)=exp(\frac{σ^2}{2}))]
色々な確率分布のモーメント母関数/確率母関数について
導出まで知りたい方はこちらをどうぞ。
【統計検定】確率分布のモーメント(積率)母関数完全ガイド|導出チートシート
ベルヌーイ分布の確率母関数
$$G(z)=E[Z^X]=\sum P(X=x)×Z^x$$
$$G(z)=P(X=0)×z^0+P(X=1)×z^1=(1-p)+pz$$
$$M_x(t)=1+p(z-1)$$
二項分布は、独立なベルヌーイ分布に従う確率変数のn回繰り返したものなので、以下のようになります。
二項分布の確率母関数
$$M_X(t)=(1+p(1+p(z-1))^n$$
幾何分布の確率母関数
ある事象が初めて観測されるまでの試行回数xに関わる確率分布ですね。
非負整数値をとります。
まず、k回目に初めて事象を観測するので、裏返すと「k-1回失敗している」となります。
事象を観測する確率をpとおくと、確率母関数は以下のように表すことができます。
$$G(s)=\sum_{k=1}^{∞}(1-p)^{k-1}p×s^{k}$$
ここで、等比数列の和の公式を思い出していただき、等比を\((1-p)s\)、初項を\(p\)とします。
$$G(s)=\frac{p}{1-(1-p)s}$$
指数分布のモーメント母関数
モーメント母関数になると、やっていることはほぼ変わりませんが、\(E[e^{tX}]\)を求めることになります。
$$M_x(t)=\int_{0}^{∞}e^{tX}×f(x)=λ\int_{0}^{∞}exp(-(λ-t)x)dx=\frac{λ}{λ-t}$$
指数分布の無記憶性について
少し箸休め的な話題ですが、指数分布の特徴の一つ「無記憶性」についてご紹介します。
時間の原点をずらしても分布は同じになるという特徴があります。
具体的にいうと、「昨日地震が起きたのだから、流石に明日は起きないだろう」という言説は誤りということです。
確率は変わらないので。
$$Exponential(x|θ)=\frac{1}{θ}exp(-\frac{x}{θ})$$
なので、仮に\(x’=x+a\)としたとき、
$$Exponential(x’|θ)=exp(-\frac{x’}{θ})$$
$$Exponential(x’|θ)∝exp(-\frac{x+a}{θ})$$
$$Exponential(x’|θ)=const×exp(-\frac{x}{θ})=Exponential(x|θ)$$
ポアソン分布のモーメント母関数
指数分布に従う事象が何回起きるか、というのがポアソン分布ですね。
ベルヌーイ分布における、二項分布のような関係性と考えてください。
$$M_x(t)=e^{λ(e^t-1)}$$
ポアソン分布について詳しく知りたい方は、以下のコンテンツをご覧ください。
一様分布のモーメント母関数
$$M_X(t)=\frac{e^{tb}-e^{ta}}{t(b-a)}$$
ベイズ、シミュレーション周りのチートシート
メトロポリスヘイスティングス法
こちらで詳しく扱っております。
【完全ガイド】MCMC法についてわかりやすく解説|ベイズ推定
元々のモチベーションで言うと、以下のベイズの定理の左辺である事後分布から直接サンプリングが難しいので、MCMC法を使ってパラメータを探索していくというものです。
$$P(X|D)dX=\frac{Pr(D|X)Pr(X)dX}{\int Pr(D|X)Pr(X)}$$
中でもMHアルゴリズムは、遷移核(現在のパラメータから次のパラメータへの移りやすさ)を提案分布に置き換えて、採択と棄却を繰り返すアルゴリズムです。
手順は以下の通りになります
①提案分布を設定する
遷移核は計算が難しいので、提案分布を使います。
ただ、当然提案分布は真の遷移核ではないので、詳細釣り合いは満たされないので下のような補正係数\(r\)を導入します。
この\(r\)について解けば良いことになります。
$$rq(X’|X)f(X’)=q(X|X’)f(X)$$
②\(q(X’|X)f(X’)>q(X|X’)f(X)\)ならば、\(r\)を使って確率的に補正をしていきます。
③一方で、上の条件式が偽であるならば、新しいパラメータを受け入れた方が詳細釣り合いを満たすので受容します。
この試行を繰り返していきます。
仮説検定周りのチートシート
母分散の信頼区間について
母分散の信頼区間を求めるときには、平方和をサンプル数でそのまま割って標準誤差を作るのではなく、自由度が\(n-1\)のカイ２乗分布を使います。
$$\frac{T^2}{χ_{0.025}^{2}}<\hat{σ}^2<\frac{T^2}{χ_{0.975}^{2}}$$
2標本の場合の検定については、以下のコンテンツでまとめています。
また、2標本の分散が異なる場合には、2標本の期待値の差を比較する意義があるのかという「ベーレンスフィッシャー問題」という議論もあります。
興味深いですね:)
【非等分散編】pythonでWelch(ウェルチ)のt検定をやってみた
時系列解析についてのチートシート
ARモデルの分散について
$$u_{t+1}=αu_{t}+ε_{t+1}$$
誤差項の\(ε_{t+1}\)がちゃんと白色雑音であると仮定します。
この時の分散を求めてみましょう。
$$V(u_{t+1})=α^2V(u_t)+V(ε_{t+1})$$
分散の場合は、係数が平方されますね。
定常という過程により、時点が違えど分散は同じという仮定をおきます。
$$σ^2_{u}=α^2σ^2_{u}+σ^2$$
$$(1-α^2)σ^2_{u}=σ^2$$
$$σ^2=\frac{σ^2}{1-α^2}$$
誤差項の分散をパラメータの平方と1との差分でスケールした値になります。
これがわかっていれば、自己相関係数が変動した時の分散の変化量がわかりますね。
【時系列】ARモデルをわかりやすく解説|Yule-Walker法や最尤法も
スペクトル密度関数
スペクトル密度関数は、ARモデルやMAモデルの周波数成分の強度を表すために使われる関数です。
以下λは周波数を表します。
AR(自己相関)モデルにおけるスペクトル密度関数は以下のように表されます。
$$f(λ)=\frac{σ^2}{2π}|1-ae^{-iλ}|^{-2}$$
定常状態(aの絶対値が1より小さい)であることが前提ですが、以下のように分類できます。
aが0に近い時：自己相関が小さいので、低周波成分と高周波成分の強度はほぼ等しい
aが1に近い時：低周波成分が強い
aが-1に近い時：高周波成分が強い
MA(移動平均)モデルにおいてはスペクトル密度関数は以下のように表されます。
$$f(λ)=\frac{σ^2}{2π}|1+be^{iλ}|^{2}$$
bの値によって、密度関数の形は以下のように分類できます。
bが0に近い時：移動平均が小さいので、低周波成分と高周波成分の強度はほぼ等しい
bが1に近い時：低周波成分が強い
bが-1に近い時：高周波成分が強い
準一級には、ラグオペレータを使ってモデルが表されることもあります。
$$L^kY_t=Y_{t-k}$$
上のように、t期時点のアウトカムをt-k時点のアウトカムを使って表せます。
これは「ラグ演算子をk回適用した状態」と呼びます。
知らないと式の意味がわからなくなるので知っておきましょう。詳しくは以下コンテンツをご覧ください。
【A/Bテストなし】競合施策の効果を推定したい|因果推論と時系列解析
ベイズ法のチートシート
ベイズ周りは教科書の最後で取り上げることもあり、対策が手薄になりがちです。
他コンテンツではベイズの定理から詳しく解説しているので、よければご覧ください。
【ベイズの定理】事後分布から推定量を導く方法について|python
正規分布の事後分布の期待値と分散について
ある正規分布\(N(μ_0,σ^{2}_0)\)を事前分布として、新しく観測値を得たとします。
その場合の事後分布の期待値や分散は、どのように変わるかという話です。
-期待値について-
$$\frac{σ^{2}_0X+(\frac{σ^2}{n}μ_0)}{σ^{2}_{0}+\frac{σ^2}{n}}$$
n：新しく得られた観測値の数を表します。
高校生の時に習いました、内分のような形を取ります。
つまり、次の観測点xと事前平均\(μ_0\)を\(σ^2_{0}:σ^2\)に内分する点だといえます。
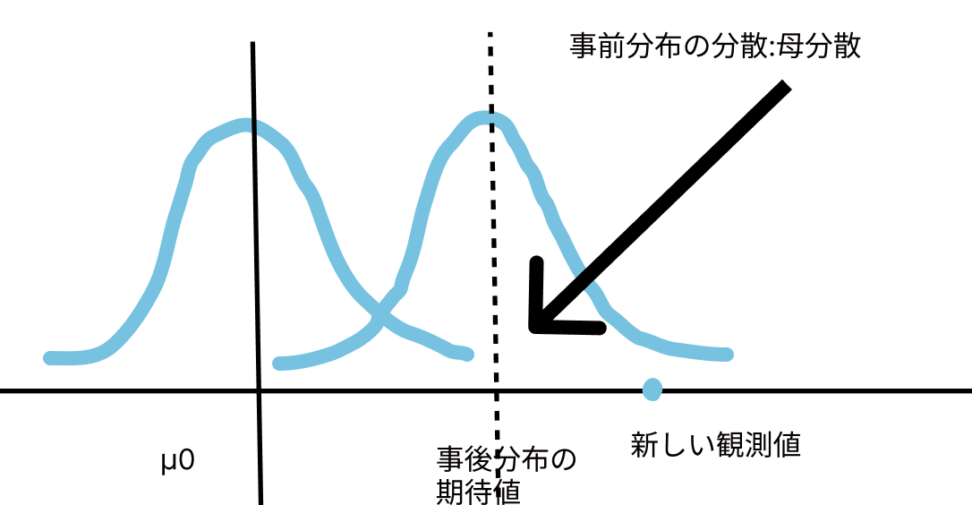
新しい観測点が、元の事前分布の期待値よりも大きく離れている場合は、大きく引っ張られてしまうということですね。
-分散-
分散は、基本的にサンプル数が増えれば(つまり、新しい観測点を得られたら)、徐々に小さくなってくということを念頭においてください。
以下のようになります。
$$(\frac{n}{σ^2}+\frac{1}{σ^2_{0}})^{-1}$$
n：新しく得られた観測値の数を表します。
おまけ｜計算テクニックや覚えておくと助かりそうな式変換など
共分散の計算について
逆になりがちですね。相関係数を求める際や、標本平均の期待値や分散を出すときに使います。
$$COV(X,Y)=E[XY]-E[X]E[Y]$$
分散の計算について
\(E[X^2]\)が求めにくい時は、こっちを使ったほうが便利です。
$$E[X(X-1)]+E[X]-(E[X])^2=V(X)$$
主成分得点の求め方について
相関行列による主成分分析の場合、主成分得点は固有値の平方根と主成分の値の積で表されます。
ただ分散共分散行列の場合は、標準偏差でスケール調整する必要があります。
$$Principal component score=\sqrt{λ}*u_i$$
主成分分析については、以下のコンテンツでご覧くださいませ。
【python】主成分分析(+回帰)の仕組みとコード例|教師なし学習
【線形代数】固有値や固有ベクトルは機械学習にどう使われているのか|主成分分析
無限等比級数について
$$\sum_{k=0}^{∞} \frac{1}{a^{k}}=\frac{a-1}{a}$$
上のような式は覚えておくと良いでしょう。
例えば、a=2として\(\sum_{k=0}^{∞} \frac{1}{2^{k+1}}\)の期待値を考えてみましょう。
\(\sum_{k=0}^{∞} \frac{1}{a^{k}}\)を一階微分すると、\(-\sum_{k=0}^{∞} \frac{k}{a^{k+1}}\)となります。
\(a=2\)なので、\(-\sum_{k=0}^{∞} \frac{k}{2^{k+1}}\)ですね。
右辺も微分してみると以下のような結果が得られます。
$$-\sum_{k=0}^{∞} \frac{k}{2^{k+1}}=-\frac{1}{(a-1)^2}$$
最後に\(a=1\)とすると、答えは1であることがわかります。
統計検定準一級のチートシートは以上になります。
反響が高かったため、2級のチートシートも作成しようと思います。
その他、青の統計学では統計学を通して機械学習のアルゴリズムを理解できるような記事を多く用意しています。
ぜひご覧ください。
【統計学】分散不均一だと何が問題なのか|不偏性とガウスマルコフ性について
【python】畳み込みニューラルネットワークによる画像判別プログラムの開発
【kaggle】ベイズ最適化とXGBでtitanicの予測問題を解く|python
【python】Ridge(リッジ)回帰で多重共線性を解決する話
