【大学数学の壁】イプシロン・デルタ論法をわかりやすく解説
なぜ極限を厳密に定義する必要があるのか
こんにちは、青の統計学です。
今回は、大学で数学の講義を受けると必ず出会うイプシロン-デルタ論法について解説します。

そもそも、極限という概念は、微分や積分を理解するための出発点として、すでに馴染み深いものでしょう。高校数学では、「限りなく近づく」という直感的な表現で極限を捉えてきました。しかし、大学でより高度な数学、特に解析学や確率論を学ぶ上で、この直感的な理解だけでは不十分なのです。
例えば、関数 $f(x)$ が $x=a$ で連続である、とはどういうことでしょうか? 直感的にはグラフが途切れていないことで十分に見えます。
ですが、数学的に厳密に、明確に定義しようとすると、この「限りなく近づく」という表現が大きな壁になります。
どれほど近ければ“限りなく”と言えるのかが人によって変わる以上、論理的な証明が一気に難しくなるのです。
この曖昧さを取り除き、極限や連続性を厳密に記述するための概念というのがイプシロン・デルタ論法($\epsilon-\delta$ 論法) ってわけです。
数学的背景
1. 極限の直感的定義には限界がある
まず、この論法の原点について、ザックリ解説をはさみましょう。
イプシロン・デルタ論法が生まれる以前、極限を「無限小」という概念を用いて扱っていました。無限小とは、0ではないが、どんな正の数よりも小さい数という、直感的ながらも曖昧な存在です。

例えば、関数 $f(x)$ の $x=a$ における極限値 $L$ を考えるとき、当時は「$x$ を $a$ に限りなく近づけるとき、$f(x)$ の値が $L$ に限りなく近づく」
という直感的な説明になっていしまいます。
この定義は、確かに便利ですが、限りなくとは具体的にどれくらいの距離を意味するのか、という問いに答えることができません。
人によって近いの感覚が異なる以上、
・極限が本当に存在するのか
・その値が唯一なのか
といった点を、正確に議論することができません。
こうも曖昧だと、数学的な議論に矛盾や誤解を生む原因になりますよね
2. $\epsilon$と$\delta$の役割
この曖昧さを排除し、極限を実数(Real Number)という具体的な数値のみを用いて定義しようとしたのが、イプシロン・デルタ論法です。この論法では、限りなく近いという概念を、任意の正の数 $\epsilon$(イプシロン)と、それに対応する正の数 $\delta$(デルタ)という、二つの具体的な距離で置き換えます。
$\epsilon$(イプシロン):目標とする近さ
$\epsilon$ は、関数値 $f(x)$ が極限値 $L$ にどれだけ近づいてほしいか、という目標の誤差範囲を表します。これは、どんなに小さな正の数であっても構いません。
例えば、$\epsilon = 0.1$ なら「$L$ から $\pm 0.1$ の範囲に入ってほしい」、$\epsilon = 0.001$ なら「$L$ から $\pm 0.001$ の範囲に入ってほしい」という意味になります。
$\delta$(デルタ):許容される近さ
$\delta$ は、$\epsilon$ という目標を達成するために、変数 $x$ を $a$ にどれだけ近づける必要があるか、という入力の許容範囲を表します。$\delta$ の値は、$\epsilon$ の値によって決まります。
3. 関数の極限の$\epsilon-\delta$定義
さて、ここからは理論的な内容に入っていきます。
定義には苦手意識のある方も多いと思いますが、一緒に頑張りましょう!
関数 $f(x)$ が $x$ を $a$ に近づけたときの極限値が $L$ である($\lim_{x \to a} f(x) = L$)とは、次の条件が成り立つことをいいます。
定義(関数の極限)
任意の正の数 $\epsilon$ に対して、ある正の数 $\delta$ が存在し、 $0 < |x – a| < \delta$ を満たすすべての $x$ について、 $|f(x) – L| < \epsilon$ が成り立つ。
$$\lim_{x \to a} f(x) = L \iff \forall \epsilon > 0, \exists \delta > 0 \text{ s.t. } 0 < |x – a| < \delta \implies |f(x) – L| < \epsilon $$
つまり、どんなに小さな誤差($\epsilon$)を要求されても、それに見合った入力の範囲($\delta$)を必ず設定できるということです。
この定義を、論理記号を使って読み解いてみましょう。
①$\forall \epsilon > 0$(任意の $\epsilon$ に対して): どんなに小さな誤差範囲($\epsilon$)を指定されても、という意味です。

これは、極限値 $L$ が唯一の値であることを証明するための、最も厳しい要求です。。
②$\exists \delta > 0$(ある $\delta$ が存在する): $\epsilon$の要求をクリアするために、適切な入力の範囲($\delta$)を必ず見つけ出せる、という意味です。
③$0 < |x – a| < \delta$: $x$ を2.で見つけ出した適切な入力の範囲($\delta$)から選ぶ、ただし、$x$ は極限を求めたい点 $a$ そのものであってはいけない、という条件です。
この条件は、極限は近づいた先の値を知りたいのであって、その点そのものの値は関係ない、ということを明確にしています。
④$\implies |f(x) – L| < \epsilon$: ($\delta$)から選んだ $x$ を関数に代入すると、その結果 $f(x)$ は必ず1.で指定された「誤差範囲」($\epsilon$)の内側に収まる
覚えておきたいことは、以下です。
同じ $\varepsilon$ を固定しても、点の位置によって必要となる $\delta$ の大きさが大きく変わります
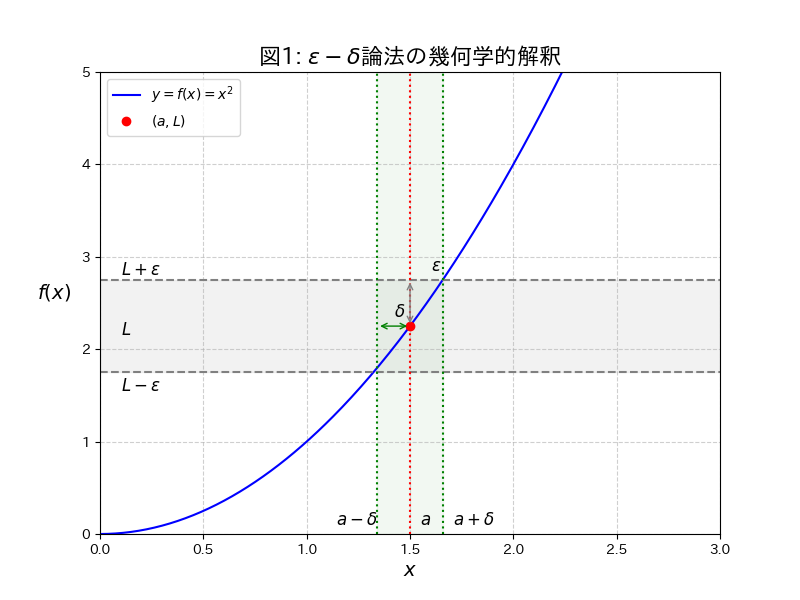

特に $x$ が 0 に近いほど $\delta$ が極端に小さくなってしまう様子がわかるかと思います。
4. 連続性の定義
極限の定義ができると、連続性も厳密に定義することができます。
関数 $f(x)$ が $x=a$ で連続であるとは、極限値と関数値が一致すること、つまり $\lim_{x \to a} f(x) = f(a)$ が成り立つことを表しています。
これを $\epsilon-\delta$ 論法で表現すると、次のようになります。
定義(連続性)
任意の正の数 $\epsilon$ に対して、ある正の数 $\delta$ が存在し、 $|x – a| < \delta$ を満たすすべての $x$ について、 $|f(x) – f(a)| < \epsilon$ が成り立つ。
極限の定義との違いは、入力の条件から$0 < |x – a|$という制約が取り除かれた点です。これは、極限の定義では、点 $a$ そのものは含めなかったが、連続性の定義では $|x – a| < \delta$ とすることで、$x=a$ の場合($|x – a| = 0$)も含めて考えることになった、ということを意味します。
$\epsilon-\delta$論法が基礎となる概念
実際にこの考えが、どう生きているのかをみていきましょう。
1. 一様連続性
連続性の定義では、$\delta$ の値は $\epsilon$ と点 $a$ の両方に依存していました。つまり、関数が連続であっても、点 $a$ が変われば、同じ $\epsilon$ に対しても $\delta$ の値は変わりうるということです。
これに対し、一様連続性は、定義域全体で $\delta$ の値が $\epsilon$ のみに依存し、点 $a$ には依存しないという、より強い条件を課します。
定義(一様連続性)
任意の正の数 $\epsilon$ に対して、ある正の数 $\delta$ が存在し、 定義域内の任意の $x_1, x_2$ について、 $|x_1 – x_2| < \delta$ ならば $|f(x_1) – f(x_2)| < \epsilon$ が成り立つ。
$$\forall \epsilon > 0, \exists \delta > 0 \text{ s.t. } \forall x_1, x_2 \in I, |x_1 – x_2| < \delta \implies |f(x_1) – f(x_2)| < \epsilon $$
補足|数値計算の安定性
通常の連続性と一様連続性のことを考えると、数値計算の安定性が見えてきます。
- 通常の連続性:ある点 $a$ の近くで、入力の小さな変化($\delta$)が出力の小さな変化($\epsilon$)に繋がることを保証します。
- 一様連続性: 定義域のどこを選んでも、入力の小さな変化($\delta$)が、出力の小さな変化($\epsilon$)に繋がることを、同じ $\delta$ で保証します。
つまり、一様連続な関数は、定義域のどこで計算しても、入力の誤差が急激に拡大することがないため、計算が安定していると言えます。機械学習における勾配降下法などの最適化アルゴリズムでは、関数の滑らかさや安定性が収束の鍵となるため、この一様連続性の概念が背後で重要な役割を果たしています。
以下の図は、関数 $f(x)=\frac{1}{x}$ が「連続ではあるが、一様連続ではない」ことを示すイメージ図です。
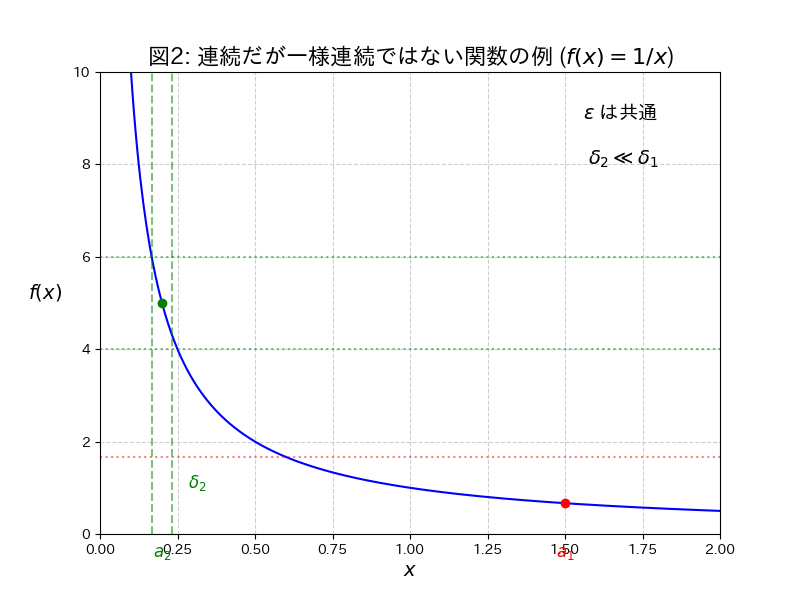

定義域である $x > 0$ の範囲(図で示されている範囲)では、どこでもグラフが途切れておらず、連続ではありそうです。
ただ、$\delta$ が場所によって大きく異なります。
緑の点($x$ が小さい、原点に近い):グラフの傾きが非常に急な場所です。ここで $f(x)$ の変化を $\epsilon$ 以内に収めるためには、$\delta_2$(横軸の緑の点線の幅の半分)は非常に小さく取る必要があります。
赤の点($x$ が大きい、原点から遠い):グラフの傾きが緩やかな場所です。ここで $f(x)$ の変化を同じ $\epsilon$ 以内に収めるためには、$\delta_1$ は $\delta_2$ よりもずっと大きく取ることができます。
つまり、$\epsilon$ を固定しても、原点に近づく($x$ が小さくなる)につれて、許容される $\delta$ の値がどんどん小さくなってしまい、共通の $\delta$ を見つけることができません。このため、この関数は一様連続ではないと判断されるというわけです。
2. 確率収束
さて、ここからは確率を用いた実践的な内容に入っていきます。
統計学では、確率変数の列が、ある値や別の確率変数に収束するという概念が頻繁に登場します。例えば、標本平均が母平均に近づくことを主張する大数の法則などがその典型です。
この収束を厳密に定義する際にも、$\epsilon-\delta$論法と同じ論理構造が用いられます。それが確率収束です。確率変数の列 $X_n$ が、ある確率変数 $X$ に確率収束する$X_n \xrightarrow{p} X$とは、次の条件が成り立つことをいいます。
確率収束
任意の正の数 $\epsilon$ に対して、 $n \to \infty$ のとき、確率 $|X_n – X| \ge \epsilon$ となる事象の確率が $0$ に収束する。
$$X_n \xrightarrow{p} X \iff \forall \epsilon > 0, \lim_{n \to \infty} P(|X_n – X| \ge \epsilon) = 0 $$
確率収束では、$\delta$ の代わりに試行回数 $n$ を無限大にすることで、誤差 $\epsilon$ 以上のズレが生じる確率を $0$ に近づけています。

直感的にいうと「どんなに小さな誤差 $\epsilon$ を設定しても、試行回数を十分に増やせば、その誤差を超えるズレが生じる確率は無視できるほど小さくなる」ということを厳密に定義しているのです。
大数の法則や中心極限定理の話はこの辺りでしています。
下の図は、コイン投げのような確率現象に対して、大数の法則がどのように働くかを可視化したイメージ図です。サンプル数 n を 10・100・1000 と増やすにつれて、標本平均の分布(赤・青・緑)が次第に狭く尖り、真の母平均 0.5(黒破線)へ収束していく様子が示されています。
これは標本数が増えるほど、平均値は真の値に近づくという確率収束の基本的な考え方を表しています。

青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!



