回帰不連続デザイン(RDD)をわかりやすく解説【因果推論】
こんにちは、青の統計学です。
さて、現場で重要かつ難しい問いの一つは、「なぜ」という因果関係の問いです。
- 「ある施策は本当に効果があったのか?」
- 「この教育プログラムは学生の成績を向上させたのか?」
このような問いに答えるためには、単なる相関関係ではなく、因果関係を突き止める必要があります。理想は、すべてをランダム化比較試験(RCT)で検証することですが、現実には倫理的、時間的、コスト的な制約から不可能です。
そこで登場するのが、自然界や社会の仕組みの中に潜む「偶然の実験」を利用する、因果推論の手法群です。その中でも準実験の一つが、今回解説する回帰不連続デザイン(Regression Discontinuity Design, RDD)です。

RDDは、ある「境界線」の存在を利用し、あたかもRCTを行ったかのような因果効果の推定を可能にする、というのがポイントです。
この記事では、因果推論の基本的な考え方は前提として進めるので、復習したい方はこちらの記事をご覧になってからがおすすめです。
RDDの数学的背景:カットオフ付近のランダム性
回帰不連続デザイン(RDD)の大事な部分は、処置(介入)の割り当てが、ある連続的な変数(割り当て変数、Running Variable: $X$)の特定の閾値(カットオフ、Cutoff: $c$)によって決定されるという状況を利用することにあります。
これだけだと意味がわからないので、ちょっと具体例で見てみましょう。
割り当て変数とカットオフ
例えば、奨学金の給付を考えてみましょう。
•割り当て変数 $X$: 前年度の成績(点数)
•カットオフ $c$: 80点
•処置 $D$: 奨学金の給付($D=1$ なら給付、$D=0$ なら不給付)
つまり、前年度の成績が80点あることを境に、奨学金がもらえる、もらえない、が変わってきます。79点の人は絶望ですね。
このとき、処置の割り当ては次のように決定されます。
$${D_i = \begin{cases} 1 & \text{if } X_i \ge c \ 0 & \text{if } X_i < c \end{cases}}$$
何が嬉しいか|局所的なランダム化の仮定
この問題設定で、何がわかるかというと、カットオフの直前と直後にいるサンプルは、その他の特性(潜在的な成績、モチベーション、家庭環境など)において、ほぼ同質であると見なせる点です。

考えてみてください。成績が79.9点だった学生と、80.1点だった学生の間には、本質的な能力や背景に大きな違いがあるでしょうか? わずか0.2点の差は、試験当日の体調や採点の誤差など、実質的にランダムな要因によって生じたと考えるのが自然です。
RDDは、このカットオフ付近の非常に狭い範囲(局所)において、処置の割り当てがランダム化されたと仮定します。つまり、カットオフの直前と直後のグループは、RCTにおける「統制群」と「処置群」に匹敵する、比較可能なグループにできます。
そもそも、なんでこの局所的なデータしか使ってはいけないか、でいうと決定的な割り当てがある場合、セレクションバイアスが生じている恐れがあり、データ全体で回帰を行うと誤った解釈を招く恐れがあるからですね。
セレクションバイアス
介入以外の属性の差によるバイアスです。
例えば、進学校には学力を伸ばす機能があるかどうか調べたときに、進学校に合格できた場合の集合と、不合格だった場合の集合でナイーブな比較をします。
このときは、「進学校による教育効果」の他にも、「もともとの学力や才能が高かったから進学校にも合格できたし、その後の学力も高かった」と言えてしまいます。
これをセレクションバイアスと呼び、介入をするかどうかをある閾値によって明確に分ける場合に発生します。
- 1,500g未満の未熟児は新生児集中治療室に入れる。1,500g以上の新生児は入れない。
- 動画を 一日3時間未満見る人には広告を見せない/3時間以上なら広告を見せる
など、例を挙げるとキリがありませんね。
因果効果の推定
この局所的なランダム化の仮定に基づき、因果効果(処置効果。今回でいうと、奨学金制度による成績の向上率のようなもの)は、カットオフ$c$における結果変数(Outcome Variable: $Y$)の期待値の不連続なジャンプとして推定されます。
$${ \tau = \lim_{x \to c^+} E[Y|X=x] – \lim_{x \to c^-} E[Y|X=x} ]$$
- $\lim_{x \to c^+} E[Y|X=x]$ は、カットオフ$c$の直後(処置を受けた側)の結果変数の期待値
- $\lim_{x \to c^-} E[Y|X=x]$ は、カットオフ$c$の直前(処置を受けなかった側)の結果変数の期待値
- $\tau$ は、カットオフ$c$における局所平均処置効果(Local Average Treatment Effect, LATE)
この推定は、割り当て変数$X$と結果変数$Y$の関係を、カットオフの前後でそれぞれ回帰分析を用いてモデル化することで行われます。
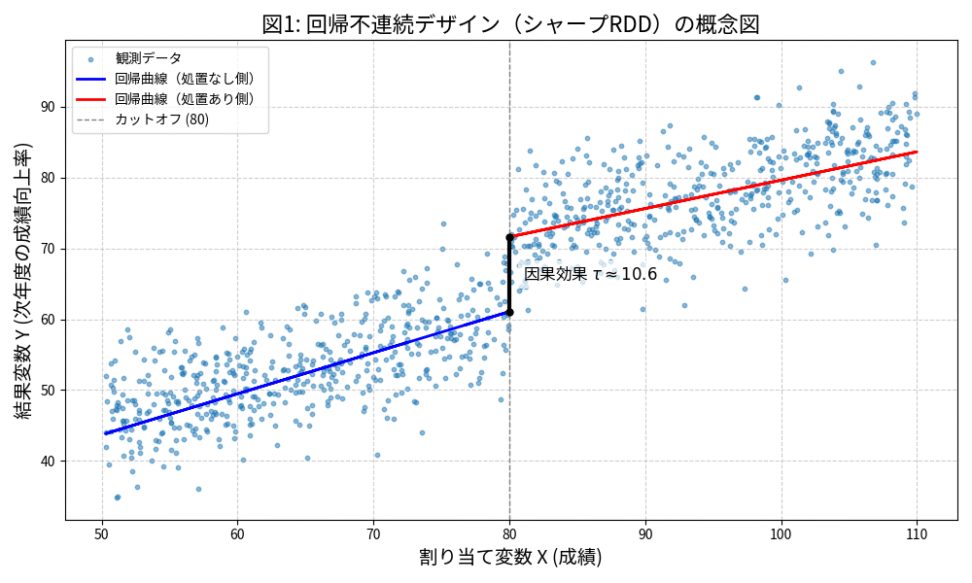
- X軸:割り当て変数(成績)
- Y軸:結果変数(次年度の成績向上率など)
カットオフ$c$(80点)を境に、Y軸の値が不連続にジャンプしている様子がわかり、カットオフ付近のデータ点で、回帰曲線(直線)が不連続に繋がっていますね。
で、RDDの推定は、最終的に「カットオフにおけるジャンプ$\tau$がゼロではない」という仮説検定に帰着します。
$${ H_0: \tau = 0 \quad \text{(帰無仮説:因果効果はない)} }$$
$${ H_1: \tau \ne 0 \quad \text{(対立仮説:因果効果がある)} }$$
つまり、「ある仮定(この場合は局所的なランダム化)の下で、観測された差(ジャンプ)が偶然起こる確率($p$値)はどれくらいか?」を問うことに等しいですね。
こう考えると、統計学の入門レベルの仮説検定の考え方が、いろんなところで作られていることがわかるはずです。
他の因果推論手法との関連性:「準実験」という立ち位置
RDDが統計学や機械学習の他の概念とどのように繋がっているかを理解してみましょう。
ランダム化比較試験(RCT)との関係
RDDは、RCTの「次善の策」として位置づけられます。
| 手法 | 処置の割り当て | 因果効果の推定範囲 | 特徴 |
| RCT | 完全にランダム | 全ての対象者(平均処置効果, ATE) | 最も強力な因果推論。しかし、実施が困難な場合が多い。 |
| RDD | カットオフによる決定論的/確率的割り当て | カットオフ付近の対象者(局所平均処置効果, LATE) | 処置の割り当てが「外生的」なルールに基づく場合に適用可能。 |
RDDの強みは、RCTが不可能な状況でも、カットオフ付近の局所的な因果効果を、RCTに匹敵する信頼性で推定できる点にあります。RCTの「ランダム化」という仮定を、カットオフ付近の「実質的なランダム性」に置き換えているからです。
RDDは、1960年代には確立されていた手法です(1980年代に確立された傾向スコアより前)が、注目する部分を狭くすることによる、データ量の少なさからくる精度の悪さがネックになっていましたが、自然実験による因果効果の推定に使えることから注目されてきました。
傾向スコアや差分の差分法(DID)との違い
RDDは、傾向スコア・マッチングや差分の差分法(DID)といった、他の観察データに基づく因果推論手法とも異なります。
傾向スコア・マッチング
処置群と統制群の共変量(背景情報)を揃えることで、比較可能性を確保しようとする手法。一方で、未観測の交絡因子(データに記録されていない要因)の影響を排除できないという根本的な弱点があります。
差分の差分法(DID)
処置群と統制群の時間的な変化の差を見ることで、共通のトレンドの影響を排除しようとする手法です。実務でも頻繁に使われます。しかし、「並行トレンドの仮定」という、処置がなかったとしても両群が同じように変化したであろうという強い仮定が必要です。この確認も結構なあなあで確認されます。
一方、RDDは、カットオフ付近の「実質的なランダム性」に依存するため、未観測の交絡因子の影響を、他の手法よりも排除できると考えられています。これは、カットオフ付近では、観測された変数も未観測の変数も、処置の有無に関わらず滑らかに変化していると仮定できるからです。
分析の時は、何を見る??|滑らかさの検証
RDDの推定が妥当であるためには、当然ですが、カットオフ付近で処置の割り当て以外のすべての要因が滑らかに変化しているという仮定が不可欠です。

ちょっと穿った見方ですが、もしカットオフを境に、処置以外の要因(例:年齢、性別、他の補助金)も不連続に変化していたら、その不連続なジャンプは処置の効果だけではないかもしれません。
この「滑らかさ」を検証するためには、以下のチェックを行います。
- 共変量の滑らかさの検証
- カットオフ付近で、年齢や収入などの共変量が不連続に変化していないかを確認します。もし不連続なジャンプがあれば、それは人々がカットオフを操作(例:成績を意図的に80点ギリギリに調整)した可能性を示唆し、RDDの妥当性が損なわれます。
- 割り当て変数の密度の検証
- カットオフ付近で、割り当て変数$X$のデータ点の密度が不連続に変化していないかを確認します。もしカットオフの直後にデータ点が集中していれば、それは人々が処置を受けるために意図的に$X$を操作した証拠であり、局所的なランダム性が崩れていることを意味します。
2は特に、マニピュレーション・テストと言います。
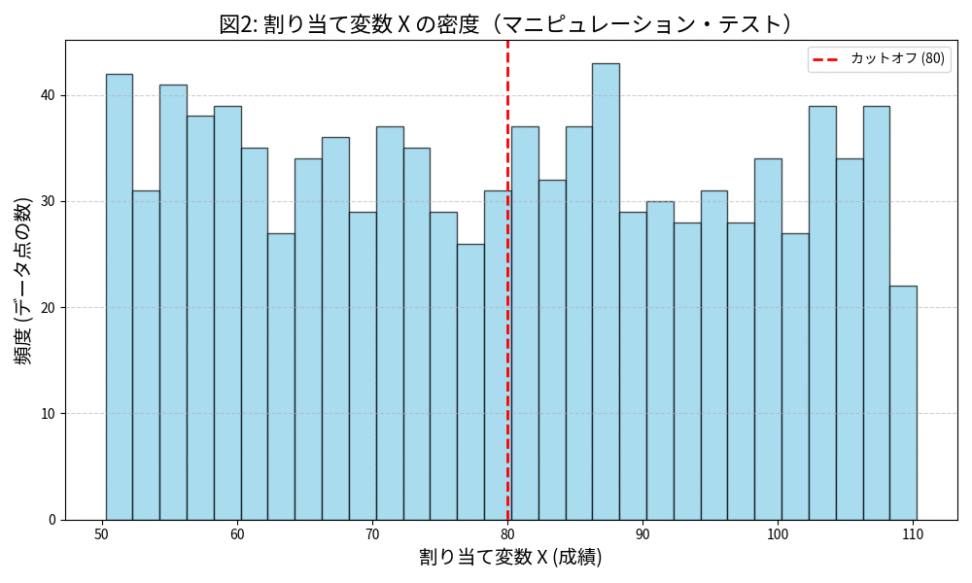
- X軸:割り当て変数(成績)
- Y軸:データ点の頻度(ヒストグラム)
カットオフ$c$(80点)付近で、頻度が不連続に変化していない(滑らかに繋がっている)様子がわかりますね。
事例|子供に対する教育機関の因果効果
このRDDは、特に論文の事例を見るのがおすすめです。
例えば、子供に対する教育機関の因果効果を分析した、成田悠輔教授の論文などが面白いです。
Regression Discontinuity in Serial Dictatorship:Achievement Effects at Chicago's Exam Schools
ByATLA ABDULKADIROGLU, JOSHUA D.ANGRIST, YUSUKE NARITA, PARAG A.PATHAK, AND ROMAN A.ZARATE
American Economic Review:Papers&Proceeding 2017 ,107(5):240-245
計量経済やEBPMの分野で特にRDDが使われている印象です。
これ以降はご自分で深ぼって欲しいのですが、経済学では、「人的資本理論」と「シグナリング理論」という対照な理論があります。
人的資本理論は、人に教育やスキルなどが蓄積されていくという理論で、学校教育の話であれば、入学した学校による教育効果で人的資本が増加したと考えます。
一方で、シグナリング理論では、学校に入学できたという事実から、その時点の才能や学力をもって学生を評価すると考えます。
この論文の結果は、学校教育による効果に有意性が認められないことから、シグナリングを示唆する内容ですね。興味が湧いた人、家族の経済学などから触れてみるといいかもしれないです。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!




