共変量シフトって結局なんなのか？｜i.i.dを正しく理解する

こんにちは、青の統計学です。

皆さんは、統計学や機械学習を学ぶ中で、「訓練データとテストデータは同じ確率分布から独立に生成される」という前提、すなわち i.i.d. (independent and identically distributed)の仮定を耳にしたことがあるでしょう。この仮定は、私たちがモデルの性能を評価し、その汎化能力を保証するための土台となっています。

しかし、現実はそんなことありません。私たちが構築したモデルを、学習時とは異なる環境や状況で運用しようとすると、途端に性能が劣化してしまう現象に頻繁に遭遇します。この「分布の変化」こそが、現場でよくある問題の一つであり、その中でも特に本質的な問題が共変量シフト (Covariate Shift)です。では、早速理論的にみていきましょう。

動画で学習したい方はこちら

なぜ「分布の変化」が機械学習を壊すのか

まず、共変量シフトがどのような状況を指すのかを明確にしましょう。

私たちが教師あり学習を行う際、入力データ（特徴量）を ${x}$、それに対応する出力データ（目的変数）を ${y}$ とします。訓練データは、ある同時確率分布 ${p_{tr}(x, y)}$ から生成され、テストデータは別の同時確率分布 ${p_{te}(x, y)}$ から生成されると考えます。

共変量シフトとは、この二つの分布が異なるにもかかわらず、入力 ${x}$ が与えられたときの出力 ${y}$ の条件付き確率分布 ${p(y|x)}$ は変化しないという特殊な状況を指します。

例えば、ある病院で開発した病気の診断モデルを、別の地域の病院で運用するケースを考えてみましょう。

• 1. 入力データ ${x}$ の変化（共変量シフト）
  • 訓練データ（開発元の病院）の患者は、平均年齢が低く、特定の生活習慣を持つ人が多いかもしれません。
  • テストデータ（運用先の病院）の患者は、平均年齢が高く、別の生活習慣を持つ人が多いかもしれません。
  • つまり、入力 ${x}$ の分布 ${p(x)}$ が ${p_{tr}(x)}$ から ${p_{te}(x)}$ へと変化しています。
• 2. 入出力の関係 ${p(y|x)}$ の不変性
  • しかし、「年齢 ${x}$ がこの値であれば、病気 ${y}$ になる確率」という生物学的な因果関係や医学的なルール自体は、病院が変わっても変化しないと仮定します。

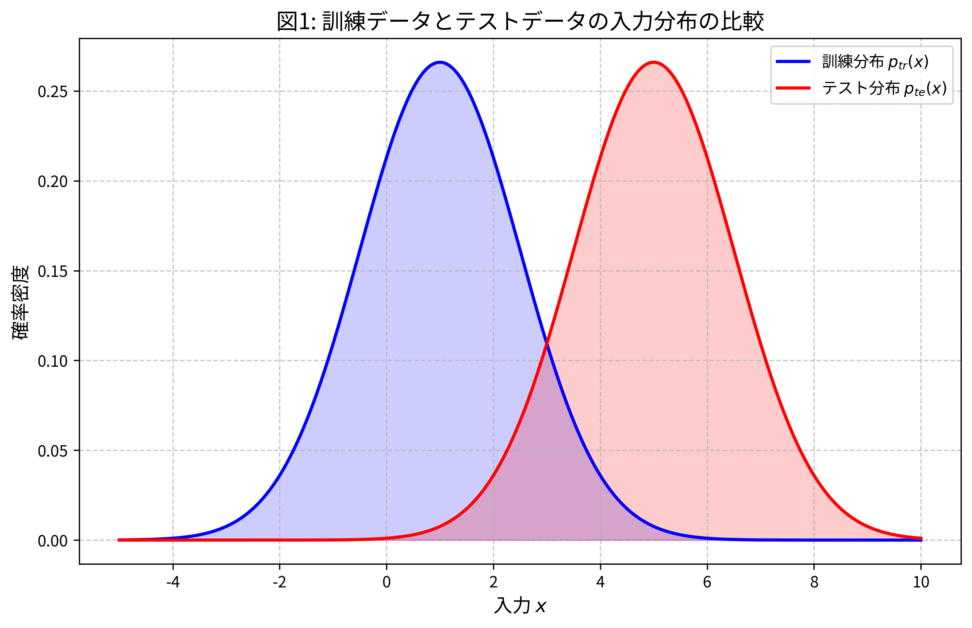
図: 訓練データとテストデータの入力分布の比較

1次元の入力 ${x}$ について、訓練分布 ${p_{tr}(x)}$ とテスト分布 ${p_{te}(x)}$ が異なる正規分布に従う様子です。訓練データがカバーしている領域と、実際に予測を行いたいテストデータの領域がズレていることがわかるかと思います。

数学的背景：期待損失の定式化とi.i.d.仮定の崩壊

なぜ、この共変量シフトが問題なのでしょうか。

すごい簡潔にいうと、モデルの性能を評価する際の「目的関数」が、i.i.d.仮定の上に成り立っているからです。

期待損失の定義

教師あり学習の目的は、真の関数 ${f(x)}$ に近い予測関数 $\hat{f}(x)$ を見つけることですね。そのために、私たちは期待損失（Expected Loss）、まあつまりリスク、と呼ばれる指標を最小化しようとします。

テストデータにおける期待損失 ${R_{te}(\hat{f})}$ は、一般に次のように定義されます。

$$R_{te}(\hat{f}) = E_{p_{te}(x, y)} [L(y, \hat{f}(x))]$$

• ${L(y, \hat{f}(x))}$ ：損失関数（例：二乗誤差 ${L(y, \hat{f}(x)) = (y – \hat{f}(x))^2}$）
• ${E_{p_{te}(x, y)}}$ ：テストデータの同時分布 ${p_{te}(x, y)}$ に関する期待値

経験損失の限界

しかし、当然ですが真の分布 ${p_{te}(x, y)}$ を知ることはできません。そこで、訓練データセット ${D_{tr} = \{(x_i^{tr}, y_i^{tr})\}_{i=1}^{n_{tr}}}$ を使って、期待損失を近似します。これが経験的な損失（Empirical Loss）です。

標準的には、訓練データにおける経験損失 ${R_{tr}(\hat{f})}$ を最小化します。

$$R_{tr}(\hat{f}) = \frac{1}{n_{tr}} \sum_{i=1}^{n_{tr}} L(y_i^{tr}, \hat{f}(x_i^{tr}))$$

i.i.d.仮定が成り立つ場合、つまり ${p_{tr}(x, y) = p_{te}(x, y)}$ の場合、訓練データの経験損失を最小化することは、テストデータの期待損失を最小化することに漸近的に繋がります。

しかし、共変量シフト下では、${p_{tr}(x) \neq p_{te}(x)}$ でした。

このとき、訓練データで最小化した経験損失 ${R_{tr}(\hat{f})}$ は、テストデータの期待損失 ${R_{te}(\hat{f})}$ の良い近似にはなりません。

図で視覚的に理解しましょう。

訓練データ（青）が左側に集中し、テストデータ（赤）が右側に集中している状況での回帰分析の結果です。訓練データのみにフィットさせた通常の最小二乗法（緑）は、データが存在しないテスト領域（右側）において、真の関数（点線）から大きく外れた予測を行ってしまいます。

オフラインテストとオンラインテストの重要性がわかりますね

ではどうするか：重要度サンプリングと密度比

では、どうすればこのバイアスを解消し、訓練データを使ってテストデータでの性能を正しく評価できるようになるのでしょうか。その鍵となるのが、重要度サンプリング考え方です。

期待損失の変形

私たちは、テストデータの期待損失 ${R_{te}(\hat{f})}$ を、訓練データの分布 ${p_{tr}(x, y)}$ を使って計算したいのです。ここで、確率論の基本的なテクニックである重要度サンプリングを適用します。

テストデータの期待損失 ${R_{te}(\hat{f})}$ を、同時分布の分解 ${p(x, y) = p(x)p(y|x)}$ を用いて書き直します。

$$R_{te}(\hat{f}) = \int L(y, \hat{f}(x)) p_{te}(x, y) dx dy$$

共変量シフトの仮定 ${p_{te}(y|x) = p_{tr}(y|x) = p(y|x)}$ を利用し、さらに ${p_{te}(x, y) = p_{te}(x)p(y|x)}$ と分解します。

$$R_{te}(\hat{f}) = \int L(y, \hat{f}(x)) p_{te}(x) p(y|x) dx dy$$

ここで、訓練データの分布 ${p_{tr}(x)}$ を分母と分子に掛けます。

$$R_{te}(\hat{f}) = \int L(y, \hat{f}(x)) \frac{p_{te}(x)}{p_{tr}(x)} p_{tr}(x) p(y|x) dx dy$$

${p_{tr}(x) p(y|x) = p_{tr}(x, y)}$ ですから、式は次のようになります。

$$R_{te}(\hat{f}) = \int L(y, \hat{f}(x)) \frac{p_{te}(x)}{p_{tr}(x)} p_{tr}(x, y) dx dy$$

この積分は、訓練データの同時分布 ${p_{tr}(x, y)}$ に関する期待値として解釈できます。

$$R_{te}(\hat{f}) = E_{p_{tr}(x, y)} \left[ L(y, \hat{f}(x)) \cdot \frac{p_{te}(x)}{p_{tr}(x)} \right]$$

重要度（密度比）の導入

ここで登場するのが、重要度または密度比（Density Ratio）と呼ばれる ${w(x)}$ です。

$$w(x) = \frac{p_{te}(x)}{p_{tr}(x)}$$

この ${w(x)}$ は、「訓練データにおける ${x}$ の出現確率に比べて、テストデータにおける ${x}$ の出現確率がどれだけ高いか」を示す比率です。

この ${w(x)}$ を使って、テストデータの期待損失を、訓練データ分布上の期待値として書き直すことができます。

$$R_{te}(\hat{f}) = E_{p_{tr}(x, y)} [ w(x) L(y, \hat{f}(x)) ]$$

重要度重み付き経験リスク最小化 (IW-ERM)

この理論に基づき、新しい経験損失を定義し、それを最小化することで共変量シフトに適応したモデル $\hat{f}$ を学習できます。

$$\min_{\theta} R_{IW}(\hat{f}) = \min_{\theta} \frac{1}{n_{tr}} \sum_{i=1}^{n_{tr}} w(x_i^{tr}) L(y_i^{tr}, \hat{f}(x_i^{tr}; \theta))$$

この手法は、重要度重み付き経験リスク最小化 (Importance Weighted Empirical Risk Minimization, IW-ERM)と呼ばれます。

なんか長ったらしいですが、かなり直感的です。

訓練データの中にあっても、テストデータでより頻繁に出現する ${x}$ に対応するデータ点（つまり ${w(x)}$ が大きい点）は、モデルの学習においてより重要であると見なされ、大きな重みが与えられます。逆に、テストデータではほとんど出現しない ${x}$ に対応するデータ点（${w(x)}$ が小さい点）は、学習への影響が小さくなります。

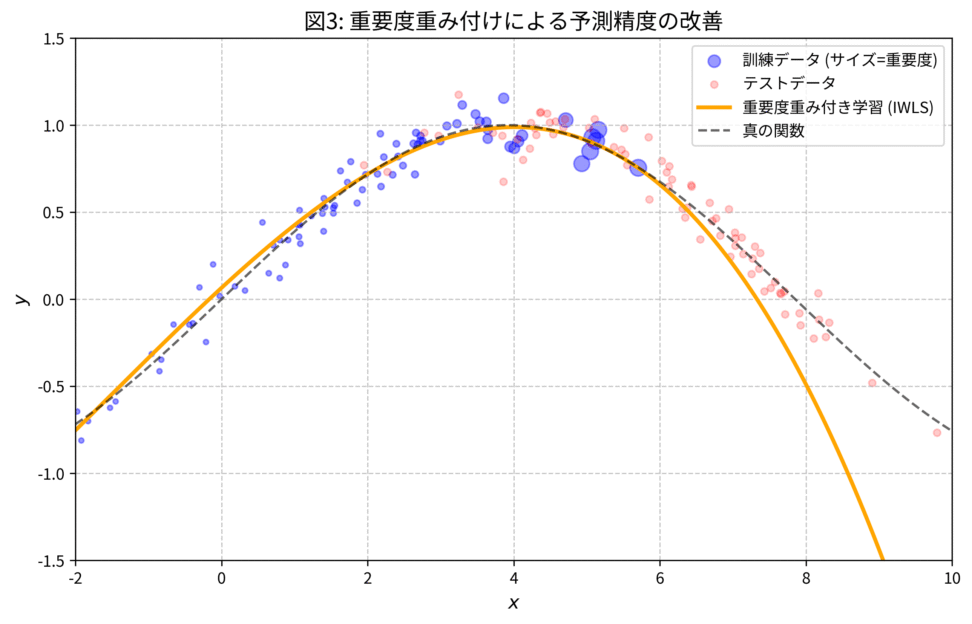
図: 重要度重み付き最小二乗法による補正

重要度 $w(x)$ に基づいて訓練データに重み付けを行った結果です。テストデータに近い領域にある訓練データほど大きな重み（円のサイズ）が与えられ、その結果、重要度重み付き最小二乗法（オレンジ）はテスト領域においても真の関数に近い予測を実現していますね。

密度比推定 (Density Ratio Estimation) の重要性

重要度重み付き経験リスク最小化 (IW-ERM) を実行するためには、重要度 ${w(x) = p_{te}(x) / p_{tr}(x)}$ を知る必要があります。しかし、私たちは ${p_{te}(x)}$ も ${p_{tr}(x)}$ も知りません。

ここで、密度比推定が登場します。これは、二つの確率密度関数 ${p_{te}(x)}$ と ${p_{tr}(x)}$ を個別に推定するのではなく、その比率 ${w(x)}$ を直接推定しようというアプローチです。

詳細には扱いませんが、アプローチの利点は、個別の密度推定に比べて、推定誤差が小さく、計算が容易になることが多い点です。

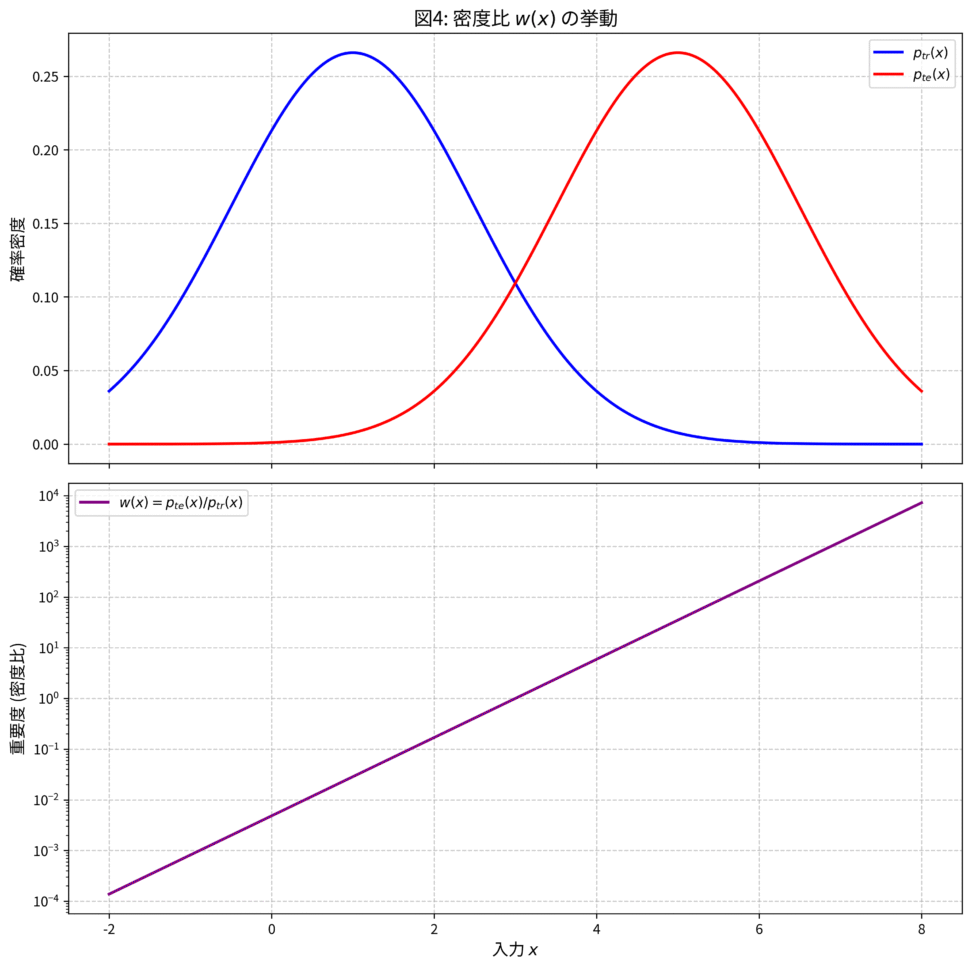
図: 密度比 $w(x)$ の挙動

上段は訓練分布とテスト分布、下段はその比である密度比（重要度） $w(x)$ を示しています。テスト分布の密度が高い領域ほど $w(x)$ の値が大きくなり、その領域の訓練データが学習において重視される仕組みが視覚的に理解できます。