ベルマン方程式をわかりやすく解説｜動的計画法

こんにちは、青の統計学です。

今回は、ベルマン方程式についてわかりやすく解説します。

ベルマン方程式とは

ベルマン方程式は、「最適性の原理」を数学的に表現したものです。

最適性の原理とは、「ある時点での最適な意思決定は、その時点から将来にわたる最適な意思決定の連鎖の一部である」という考え方です。

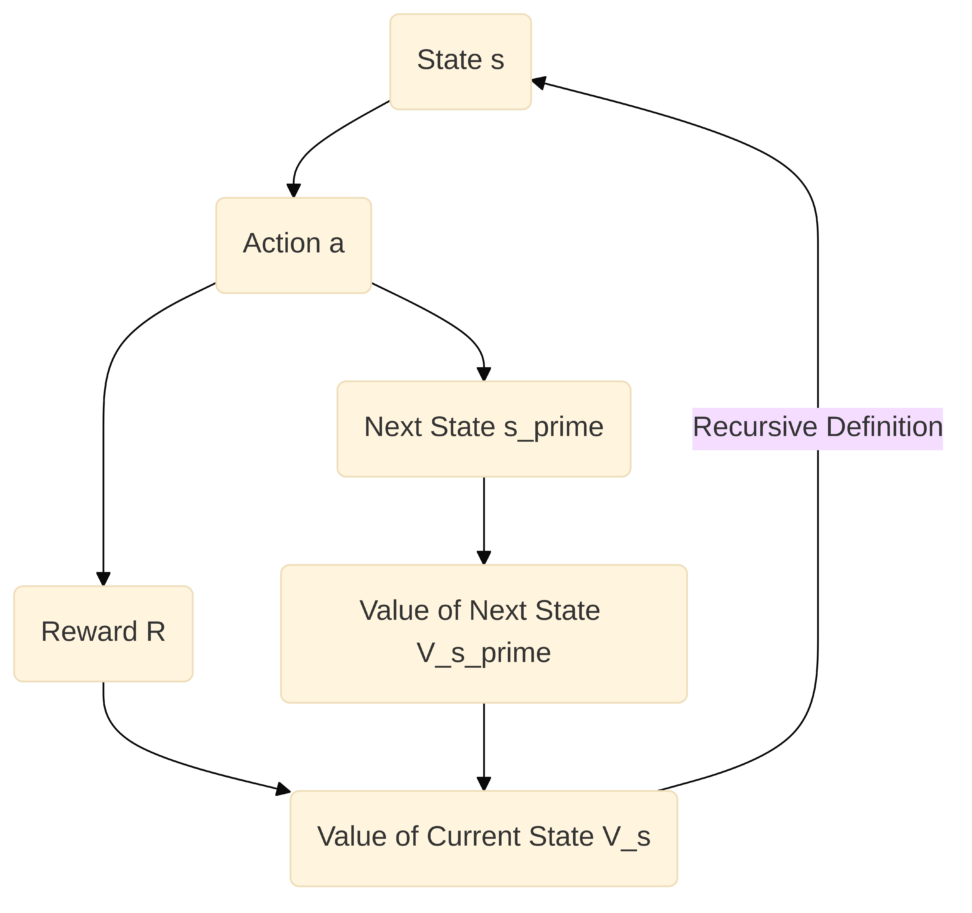
ややこしめに言うと、ある状態における最適な価値は、その状態から取りうる行動と、その行動によって到達する次の状態の最適な価値によって再帰的に定義される、ということですね。

事前準備｜マルコフ決定過程（MDP）との関係

さて、しっかりと理解するために事前知識をまとめていきます。

ベルマン方程式や動的計画法が適用される問題の多くは、マルコフ決定過程（Markov Decision Process, MDP）として定式化されます。MDPは、意思決定者が不確実な環境の中で、連続的に意思決定を行う状況を数学的にモデル化したものです。

MDPは以下の要素で構成されます。

• 状態 (State) $S$: 環境の現在の状況を表します。
• 行動 (Action) $A$: エージェントが各状態で取りうる行動の集合です。
• 遷移確率 (Transition Probability) $P(s’|s, a)$: 状態 $s$ で行動 $a$ をとったときに、次の状態が $s’$ になる確率です。
  • MDPの「マルコフ性」とは、次の状態が現在の状態と行動のみに依存し、それ以前の履歴には依存しないという性質を指します。
• 報酬関数 (Reward Function) $R(s, a)$: 状態 $s$ で行動 $a$ をとったときに得られる即時的な報酬です。
• 割引率 (Discount Factor) $\gamma$: 未来の報酬の現在価値を調整する係数です。

ベルマン方程式は、まさにこのMDPの枠組みの中で、最適な価値関数や方策を求めるための中心的な役割を果たします。

事前準備｜価値関数とは何か？

ベルマン方程式を理解する上で、まず「価値関数」という概念を考えてみましょう。

価値関数とは、ある「状態」がどれだけ「良い」か、あるいはある「行動」がどれだけ良いかを数値で表現したものです。

強化学習の文脈では、主に以下の2種類の価値関数が用いられます。

• 状態価値関数$V(s)$
  • ある状態 $s$ にいるときに、そこから最適な方策（行動の選択ルール）に従って行動し続けた場合に、将来得られる報酬の総和（期待値）を表します。
  • その状態がどれだけ「有利」であるかを示す指標
• 行動価値関数$Q(s, a)$
  • ある状態 $s$ で特定の行動 $a$ をとった後、そこから最適な方策に従って行動し続けた場合に、将来得られる報酬の総和（期待値）を表します。
  • ある状態である行動をとることがどれだけ「得策」であるかを示す指標

これらの価値関数は、未来の報酬を最大化するための方針となるわけです。

ベルマン方程式の導出と意味

では、この価値関数がどのように「最適性の原理」と結びつくのでしょうか。

ベルマン方程式は、状態価値関数 $V(s)$ と行動価値関数 $Q(s, a)$ の間に成り立つ関係式であり、最適な価値を再帰的に定義します。

状態価値関数

状態価値関数 $V(s)$ のベルマン方程式は、以下のように表現されます。

$$V(s) = \max_{a} \left( R(s, a) + \gamma \sum_{s’} P(s’|s, a) V(s’) \right)$$

• $V(s)$：現在の状態 $s$ における最適な状態価値。
• $R(s, a)$：状態 $s$ で行動 $a$ をとったときに即座に得られる報酬。
• $\gamma$：割引率（0から1の間の値）。未来の報酬を現在の価値に換算するための係数です。$\gamma$ が1に近いほど未来の報酬を重視し、0に近いほど現在の報酬を重視します。
  • 遠い未来の報酬よりも近い未来の報酬の方が不確実性が低い、あるいは価値が高いと考える経済学的な視点と共通しています。
• $P(s’|s, a)$：状態 $s$ で行動 $a$ をとったときに、次の状態が $s’$ になる確率。
  • 環境のダイナミクス（状態の遷移ルール）を表します。
• $\max_{a}$：取りうる全ての行動 $a$ の中で、括弧内の値を最大にする行動を選択するという意味です。
  • これが「最適性」を保証する部分ですね。

ちょっとこれだけだと流石にわかりにくいと思うので、国語的に整理すると、

「ある状態 $s$ の最適な価値は、その状態 $s$ で取りうる全ての行動 $a$ の中から、即座に得られる報酬 $R(s, a)$ と、その行動によって到達する次の状態 $s’$ の最適な価値 $V(s’)$ を、遷移確率 $P(s’|s, a)$ と割引率 $\gamma$ を考慮して合計したものの最大値である」

となります。

つまり、今いる場所の価値は、今できる最善の行動と、その行動がもたらす次の場所の最善の価値によって決まる、というわけです。

行動価値関数

行動価値関数 $Q(s, a)$ のベルマン方程式も同様に表現できます。

$$Q(s, a) = R(s, a) + \gamma \sum_{s’} P(s’|s, a) \max_{a’} Q(s’, a’)$$

こっちも国語的に整理すると、「ある状態 $s$ で行動 $a$ をとったときの最適な行動価値は、即座に得られる報酬 $R(s, a)$ と、その行動によって到達する次の状態 $s’$ で取りうる最適な行動 $a’$ をとった場合の最適な行動価値 $Q(s’, a’)$ を、遷移確率 $P(s’|s, a)$ と割引率 $\gamma$ を考慮して合計したものである」

ということを示しています。

割引率の役割

ベルマン方程式において、割引率について掘り下げてみます。

割引率 $\gamma$は、未来の報酬をどれだけ重視するかを調整するパラメータです。

例えば、今日の100万円と1年後の100万円では、通常、今日の100万円の方が価値が高いと感じるでしょう。これは、時間とともに価値が減少するという「時間の割引」の考え方です。

割引率が0に近いほど、エージェント（意思決定の主体）は目先の報酬を重視するようになり、1に近いほど、遠い未来の報酬も考慮に入れるようになります。この割引率を設定することで、短期的な視点と長期的な視点のバランスを取りながら、最適な意思決定を行うことができるのです。

動的計画法

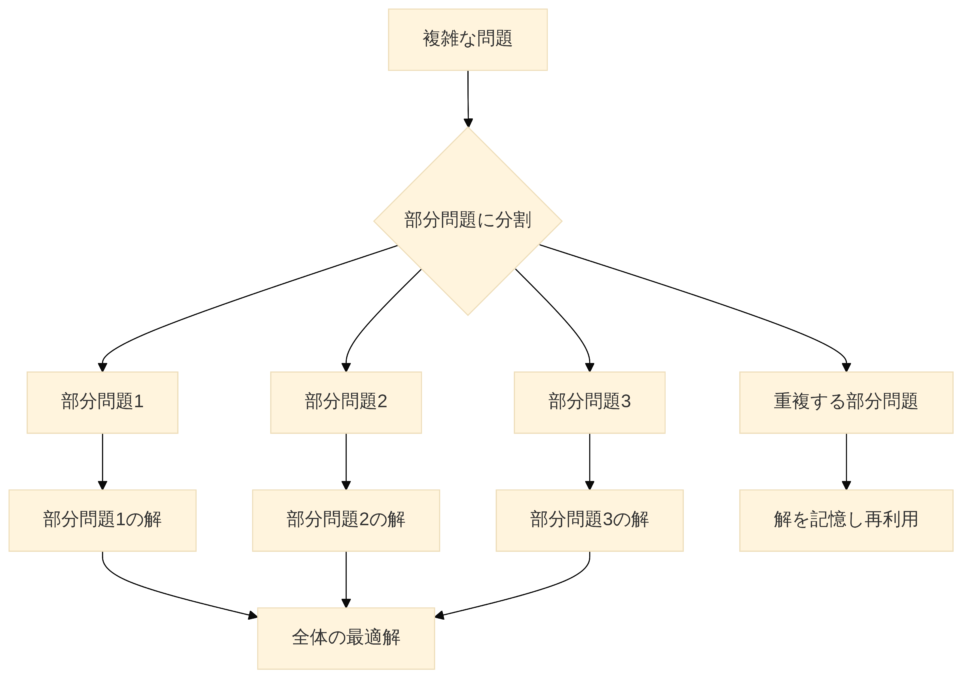
で、動的計画法とは何なのかというと、ベルマン方程式が「最適性の原理」を数学的に表現したものであるならば、そのベルマン方程式を実際に「解く」ためのアルゴリズムの枠組みです。

動的計画法は、統計学だと時系列データ解析におけるカルマンフィルターなど、確率的なモデルを用いた推論問題の最適化に利用されます。過去の観測と現在の状態に基づいて未来の状態を予測し、その予測の最適性を評価するために、ベルマン方程式の考え方を応用しています。

【時系列】状態空間モデルをわかりやすく解説|カルマンフィルタの仕組み

部分構造の最適性と重複部分問題

動的計画法が適用できる問題には、主に二つの特徴があります。

これを効率的に処理するのが動的計画法の強みです。

動的計画法のアルゴリズム：価値反復法と方策反復法

強化学習の文脈では、ベルマン方程式を解くための動的計画法のアルゴリズムとして、主に「価値反復法（Value Iteration）」と「方策反復法（Policy Iteration）」が用いられます。

これらは、前述したマルコフ決定過程（MDP）における最適な方策や価値関数を見つけるための手法です。

価値反復法（Value Iteration）

価値反復法は、ベルマン最適方程式（最適な価値関数を求めるベルマン方程式）を繰り返し適用することで、価値関数を収束させていくアルゴリズムです。

最初はランダムな価値関数から始め、各状態の価値をベルマン方程式に従って更新していきます。この更新を繰り返すことで、最終的に最適な価値関数 ${V^*(s)}$ が得られます。最適な価値関数が得られれば、各状態においてどの行動が最も価値を高めるかを選択することで、最適な方策 ${{\pi}^*(s)}$ を導き出すことができます。

価値反復法の更新式は以下のようになります。

$${V_{k+1}(s) = \max_{a} \left( R(s, a) + \gamma \sum_{s’} P(s’|s, a) V_k(s’) \right)}$$

${V_k(s)}$ は ${k}$ 回目の反復における状態 ${s}$ の価値関数です。

この式を繰り返し適用することで、${V_k(s)}$ は最適な価値関数 ${V^*(s)}$ に収束していきます。

方策反復法（Policy Iteration）

方策反復法は、以下の2つのステップを交互に繰り返すことで、最適な方策と価値関数を同時に見つけていくアルゴリズムです。

①方策評価（Policy Evaluation）

現在の方策 ${{\pi}(s)}$ の下での価値関数 ${V^{\pi}(s)}$ を計算します。これは、現在の方策に従って行動し続けた場合に、各状態がどれくらいの価値を持つかを評価するステップです。この計算には、ベルマン期待方程式（特定の方策の下での価値関数を求めるベルマン方程式）が用いられます。

$${V^{\pi}(s) = R(s, \pi(s)) + \gamma \sum_{s’} P(s’|s, \pi(s)) V^{\pi}(s’)}$$

この式を繰り返し適用することで、現在の方策 ${{\pi}(s)}$ に対応する価値関数 ${V^{\pi}(s)}$ が収束します。

②方策改善（Policy Improvement）

方策評価で得られた価値関数 ${V^{\pi}(s)}$ を用いて、現在の方策を改善します。具体的には、各状態において、${V^{\pi}(s)}$ を最大化するような行動を選択するように方策を更新します。つまり、「今の方策よりも良い行動はないか？」を探し、あればその行動に切り替えるわけです。

$${{\pi}_{new}(s) = \arg\max_{a} \left( R(s, a) + \gamma \sum_{s’} P(s’|s, a) V^{\pi}(s’) \right)}$$

これらのステップを、方策がこれ以上改善されなくなるまで繰り返すことで、最終的に最適な方策 ${{\pi}^*(s)}$ と最適な価値関数 ${V^*(s)}$ が得られます。

価値反復法と方策反復法は、どちらも最適な解に到達しますが、収束の仕方に違いがあります。価値反復法は価値関数を直接更新するのに対し、方策反復法は方策と価値関数を交互に更新します。

ベルマン方程式の導出

解説はここまでです。

計算過程まで知りたい方はこれ以降を見てください。

状態価値関数と行動価値関数

先ほど、パッと出した数式ですが、導出もしてみます。

導出には、同時確率と条件付き期待値の知識が必要ですが、予備知識はあるものとします。

とはいえ、遷移確率を周辺化してポリシーファンクションを作るだけで特にトリッキーな部分はないです。

遷移確率と方策(ポリシー)

状態Sで行動aを取ったときに状態\(S’\)に遷移する確率です。

$$P(s’|s,a)=P(s’=s(t+1)|s=s(t),a=a(t))$$

取り得る全ての行動について足し合わせると、状態\(S\)から\(S’\)への遷移確率になります。

ここで周辺化をしています。

$$P^{\pi}(s’|s)=\sum_{a}P(s’|s,a) P(a|s)=\sum_a\pi(a|s)P(s’|s,a)$$

ここで，状態\(S\)において行動\(a\)を選択する確率は方策と呼ばれ，特別に\(π\)と書きます。

$$\pi(a|s)=P(a|s)$$

即時価値と累積価値

$$\displaystyle{ R(t)=r(t+1)+\gamma r(t+2)+\gamma^2 r(t+3)+\cdots=\sum_{k=0}^\infty \gamma^k r(t+k+1) }$$

\(γ\)は割引率と呼びます。

これは第1項と残りを分けることで再帰的に書くことができます。

$$\begin{align} R(t)&=r(t+1)+\gamma \left(r(t+2)+\gamma r(t+3)+\cdots\right)\\ &=r(t+1)+\sum_{k=0}^\infty \gamma^k r(t+k+2) \\ &=r(t+1)+\gamma R(t+1) \end{align}$$

ここの理解が結構難しいと思います。

ちなみに\(r=r(t+1)\)は，行動\(a\)によって，状態\(s=s(t)\)から状態\(s′=s(t+1)\)になったときに得る即時報酬です。

なぜ、第1項と残りを分けたかというと、即時価値と将来価値を分けるためです。

もっとわかりやすく言えば、エージェントは目先の利益を最大化するだけではなく、将来にわたって利得の合計を最大化するのです。

ただ時刻\(t\)において\(t+1\)期の報酬などわかるわけないので、割引率\(γ\)をかけて報酬を割り引く必要があるというわけです。

さて、ここまで話した即時価値の期待値をとってみましょう。

$$R(s,a,s’)=E_P [r(t+1)|s’,s,a]=\sum_{rr}P(r|s’,s,a)$$

状態\(s\)での報酬の期待値は，上記の量を行動\(a\)と次の状態\(s′\)について期待値を取ります。

→要するに，行動や次の状態にかかわらず，「ただ状態\(s\)にいるだけで」これくらいの報酬が得られるだろうと期待できるということです。

ここで重みとして用いる確率は，\(a\)を取る確率と，\(s′\)となる確率なのだから，先ほど導出した方策(ポリシー)と遷移確率ですね．

$$R^\pi (s)=\sum_{a,s’}\pi(a|s)P(s’|s,a)R(s,a,s’)$$

さて、話を発展させていきましょう。

ある状態における、累積報酬の期待値を取ると、その状態を評価できると思います。

これを状態価値関数と呼びます。

$$V^\pi(s)=E_{P, \pi}[R(t)|s]$$

ここでの添字\(P\)と\(π\)の意味は，さきほど出て来た即時報酬の期待値と同様に，遷移確率\(P\)と方策\(π\)で期待値を取っているという意味です。

さて、この状態価値関数とは別に「今の状態で行動\(a\)をとった時の累積報酬の期待値」も考えねばなりません。

これを行動価値関数と呼びます。

$$Q^\pi(s,a)=E_P[R(t)|s,a]$$

$$V^\pi(s)=E_{P, \pi}[R(t)|s]=\sum_aE_P[R(t)|s,a]P(a|s)=\sum_a\pi(a|s)E_P[R(t)|s,a]$$

ここの変換でつまづいた方は、遷移確率の周辺化の部分をもう一度読み直してみてください。

最右辺の条件付き期待値は\(Q\)なので、

行動価値関数と状態価値関数の関係は以下のようになります。

$$V^\pi(s)=\sum_a\pi(a|s)Q^\pi(s,a)$$

ベルマン方程式とマルコフ性

ここまでで、状態価値関数と行動価値関数の関係は分かりましたが、まだベルマン方程式ではないです。

大雑把にやることとしては、次の状態\(s’\)で条件づけることです。

なぜでしょうか？

ベルマン方程式の導出において、状態 \(s\)から次の状態\(s’\) を条件付けする理由は、マルコフ決定過程の性質から来ています。

マルコフ決定過程では、現在の状態と行動が与えられた時、次の状態と報酬はそれらにのみ依存し、過去の履歴には依存しない（マルコフ性）という前提があります。

$$Pr(X_{n+1}=j|X_{n},X_{n-1},…,X_0)=Pr(X_{n+1},X_n=i)$$

この性質により、次の状態 \(s\) とその時の報酬を考慮することで、現在の状態\(s’\)の価値を計算することが可能になります。

マルコフ性については、以下のコンテンツでまとめています。

状態価値関数のベルマン方程式の導出

さて、状態価値関数(以下V)のベルマン方程式から導出していきます。

Vについてのベルマン方程式とQについてのベルマン方程式が両方導出できる理由は、これらが異なる視点（状態の価値 vs. 特定の行動を取った時の価値）から同じマルコフ決定過程をモデル化しているためです。

Vは状態の価値のみを考慮し、Qは特定の行動を取った場合の価値を考慮しますが、どちらも同じプロセス（MDP）に基づいております。

$$V^\pi(s)=E_{P, \pi}[R(t)|s] =\sum_a\pi(a|s)E_P[R(t)|s,a]$$

もともと上の式でした。

さて、では条件づけてみましょう。

$$E_P[R(t)|s,a]=\sum_{s’} E_P[R(t)|s’,s,a]P(s’|s,a)$$

$$\begin{align} V^\pi(s) &=E_{P, \pi} [R(t)|s] \\ &=\sum_a\pi(a|s)E_P[R(t)|s,a] \\ &=\sum_{a,s’}\pi(a|s)P(s’|s,a)E_P[R(t)|s’,s,a] \end{align}$$

累積報酬\(R(t)\)は、一期先の利得と分けて\(R(t)=r(t+1)+\gamma R(t+1)\)とかきましたね。

$$\begin{align} V^\pi(s)&=\sum_{a,s’}\pi(a|s)P(s’|s,a)E_P[R(t)|s’,s,a] \\ &=\sum_{a,s’}\pi(a|s)P(s’|s,a)E_P[r(t+1)+\gamma R(t+1)|s’,s,a] \\ &=\sum_{a,s’}\pi(a|s)P(s’|s,a)\left(E_P[r(t+1)|s’,s,a]+E_P[\gamma R(t+1)|s’,s,a]\right) \end{align}$$

右の方の\(E_P[\gamma R(t+1)|s’,s,a]\)は、即時報酬の期待値ですね。

こちらも先程は、\(R(s,a,s’)=E_P [r(t+1)|s’,s,a\)と書きましたね。

$$\begin{align} V^\pi(s)&=\sum_{a,s’}\pi(a|s)P(s’|s,a)\left(E_P[r(t+1)|s’,s,a]+E_P[\gamma R(t+1)|s’,s,a]\right) \\ &=\sum_{a,s’}\pi(a|s)P(s’|s,a)\left(R(s,a,s’)+E_P[\gamma R(t+1)|s’,s,a]\right) \end{align} $$

もう一息です！

式の一部を、\(\sum_{a,s’}\pi(a|s)P(s’|s,a)R(s,a,s’)=R^{\pi} (s)\)のように、\(s’\)における累積報酬として簡単に表せますね。

$$\displaystyle{ V^\pi(s)=R^\pi (s)+\sum_{a,s’}\pi(a|s)P(s’|s,a)E_P[\gamma R(t+1)|s’,s,a] }$$

この第2項目には遷移確率が含まれているから，方策\(a\)で条件づけているところは消せます。

加えて、期待値に関係のない\(γ\)は外に出しちゃいましょう。

$$\displaystyle{ \sum_{s’}\left(\sum_{a}\pi(a|s)P(s’|s,a)\right)E_P[\gamma R(t+1)|s’,s,a]=\gamma \sum_{s’}P^\pi(s’|s)E_P[R(t+1)|s’,s,a] }$$

さて、\(E_P[R(t+1)|s’,s,a] \)は、方策と状態2つで条件づけていますが、\(R(t+1)\)という状態\(s′=s(t+1)\)から\(s″=s(t+2)\)となった時点以降の累積報酬のことです。

マルコフ性により、これは履歴にあたる、状態\(s\)と行動\(a\)には依存しません。

そういうわけで上の式の中の条件付き期待値は，\(E_P[R(t+1)|s’,s,a]=E_P[R(t+1)|s’]=V^\pi (s’)\)という、次の状態の状態価値観数になりました。感動。

$$V^\pi(s)=R^\pi (s)+\gamma \sum_{s’}P^\pi(s’|s)V^\pi (s’)$$

つまり、これが状態価値関数におけるベルマン方程式です。

応用の話で言うと、価値反復アルゴリズムでは、価値関数 \(V(s)\)が収束するまで繰り返し更新されます。

各繰り返しで、ベルマン方程式を使って、各状態における価値の推定値を更新します。

これを、価値反復アルゴリズム（Value Iteration)と呼びます。

行動価値関数のベルマン方程式の導出

こちらの導出もやることは同じで、\(s’\)に対しての和をとってあげます。

やや説明を省略しますが、

・マルコフ性を使い、履歴で条件づけている部分は消す

・即時報酬と累積報酬の分解

・周辺化と条件づけはセットで行う

を意識すれば理解できるはずです。

$$\begin{align} Q^\pi(s,a)&=E_P[R(t)|s,a] \\ &=\sum_{s’}P(s’|s,a)E_P[R(t)|s,a,s’] \\ &=\sum_{s’}P(s’|s,a)E_P[r(t+1)+\gamma R(t+1)|s,a,s’] \\ &=\sum_{s’}P(s’|s,a)E_P[r(t+1)|s,a,s’]+\sum_{s’}P(s’|s,a)E_P[\gamma R(t+1)|s,a,s’] \\ &=\sum_{s’}P(s’|s,a)R(s,a,s’)+\gamma \sum_{s’}P(s’|s,a)E_P[R(t+1)|s,a,s’] \\ &=\sum_{s’}P(s’|s,a)R(s,a,s’)+\gamma \sum_{s’}P(s’|s,a)E_P[R(t+1)|s’] \\ &=\sum_{s’}P(s’|s,a)R(s,a,s’)+\gamma \sum_{s’}P(s’|s,a)V^\pi(s’) \end{align} $$

VとQの関係より、状態は変わっても\(V^\pi(s’)=\sum_{a’}\pi(a’|s’)Q^\pi(s’,a’)\)なので、

$$\begin{align} Q^\pi(s,a)&=\sum_{s’}P(s’|s,a)R(s,a,s’)+\gamma \sum_{s’}P(s’|s,a)\sum_{a’}\pi(a’|s’)Q^\pi(s’,a’) \\&=\sum_{s’}P(s’|s,a)R(s,a,s’)+\gamma \sum_{s’}\sum_{a’}\pi(a’|s’)P(s’|s,a)Q^\pi(s’,a’) \end{align} $$

これが行動価値関数のベルマン方程式になります。