スペクトラルクラスタリングとは?非線形データの分類
スペクトラルクラスタリングとは
スペクトラルクラスタリングは、データポイント間の類似性に基づいてデータをグループ化する教師なし学習のアルゴリズムです。
特に類似性をグラフとして捉える、というのが特徴ですね。
従来のクラスタリング手法(例:k-means)とは異なり、スペクトラルクラスタリングはデータの潜在的な非線形構造を捉えることができます。
名前の「スペクトラル」は、このアルゴリズムが類似度行列(または隣接行列)の固有値分解(スペクトル分解)に基づいているためです。

クラスタリング可視化ツールでもシミュレーションできますが、これだけちょっと処理が重いのも固有値分解しているからです。
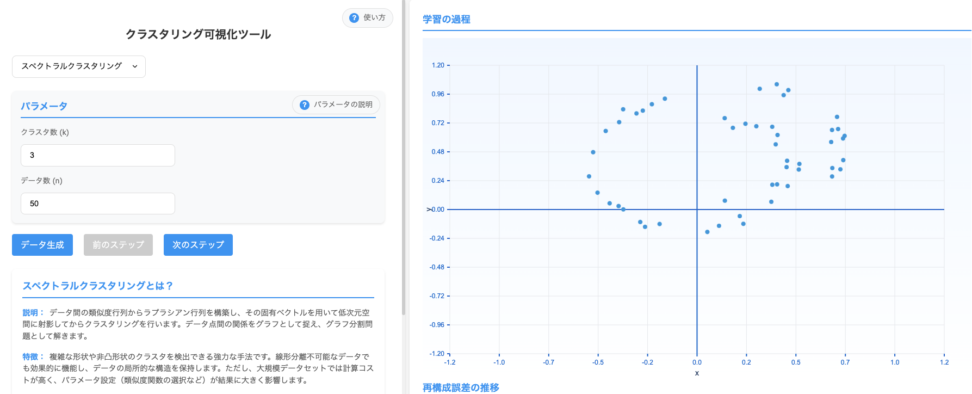
このアルゴリズムの本質は、高次元のデータを低次元の空間に変換することにあります。この変換により、クラスタの識別が容易になるような空間でデータを表現します。
スペクトラルクラスタリングの数学的背景
スペクトラルクラスタリングの理論的基盤を理解するには、グラフ理論と線形代数についての知識が必要です。
まず、データセットを重み付き無向グラフとして表現します。このグラフでは、各データポイントがノードとなり、エッジの重みがノード間の類似度を表します。
類似度グラフの構築
データポイント間の類似度を計算する一般的な方法は、ガウシアンカーネル(RBFカーネル)を使用することです
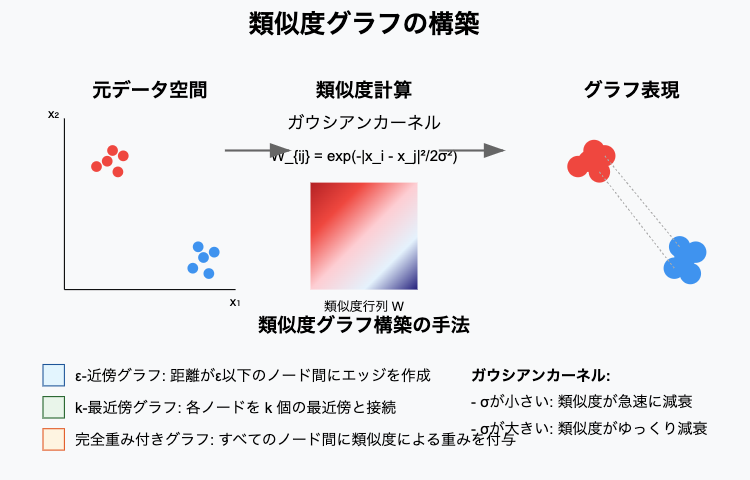
$${W_{ij} = \exp\left(-\frac{|x_i – x_j|^2}{2\sigma^2}\right)}$$
- $W_{ij}$ はノード $i$ と $j$ の間の類似度(重み)
- $|x_i – x_j|$ はデータポイント $x_i$ と $x_j$ のユークリッド距離
- $\sigma$ はカーネルのバンド幅パラメータで、類似度の減衰速度を制御します
類似度グラフを構築する主な方法
- ε-近傍グラフ
- 距離が閾値ε以下のノード間にのみエッジを作成します
- k-最近傍グラフ
- 各ノードを、その k 個の最近傍と接続します
- 完全重み付きグラフ
- すべてのノード間にエッジを作成し、類似度による重みを付けます
ラプラシアン行列
グラフが構築されると、次にラプラシアン行列 $L$ を計算します。グラフラプラシアンにはいくつかの種類がありますが、一般的なものを紹介します
- 非正規化ラプラシアン
- $L = D – W$
- 正規化ラプラシアン(対称型)
- $L_{sym} = D^{-1/2}LD^{-1/2} = I – D^{-1/2}WD^{-1/2}$
- ランダムウォークラプラシアン
- $L_{rw} = D^{-1}L = I – D^{-1}W$
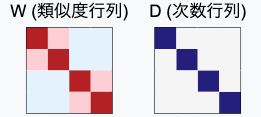
- $W$ :類似度行列(重み行列)
- $D$ :次数行列で、各ノードの接続の強さの合計を対角成分に持つ対角行列です
- ($D_{ii} = \sum_j W_{ij}$)
- $I$ :単位行列
固有値分解とクラスタリング
スペクトラルクラスタリングの核心部分は、ラプラシアン行列の固有値分解です。
この分解から得られる固有ベクトルが、データの低次元表現を提供します。
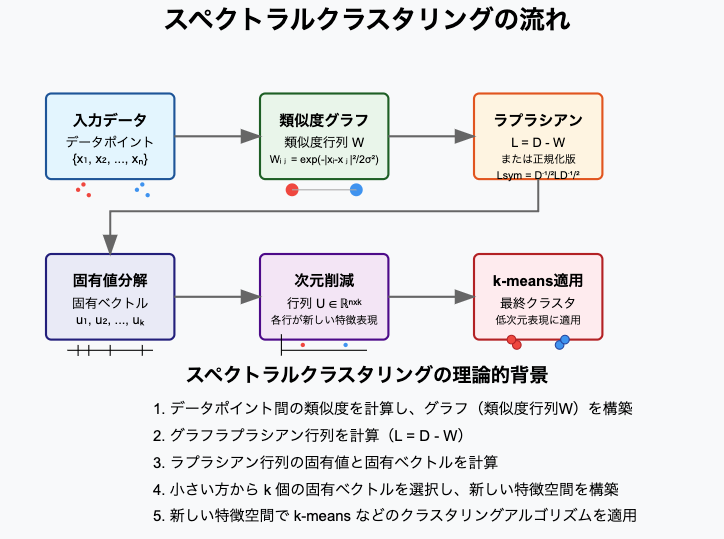
[手順]
- ラプラシアン行列 $L$ の固有値と固有ベクトルを計算します
- 最小の $k$ 個の固有値(ゼロを除く)に対応する固有ベクトルを選択します
- これらの固有ベクトルを列として持つ行列 $U \in \mathbb{R}^{n \times k}$ を形成します
- $U$ の各行をデータポイントの新しい特徴表現とみなします
- この低次元表現に k-means などの標準的なクラスタリングアルゴリズムを適用します
正規化ラプラシアンを使用した場合、アルゴリズムは以下のようになります
- 類似度行列 $W$ を計算し、次数行列 $D$ を求めます
- 正規化ラプラシアンを計算します
- $L_{sym} = I – D^{-1/2}WD^{-1/2}$
- $L_{sym}$ の最小の $k$ 個の固有値に対応する固有ベクトル $u_1, u_2, …, u_k$ を求めます
- 行列 $U = [u_1, u_2, …, u_k] \in \mathbb{R}^{n \times k}$ を形成します
- $U$ の各行を正規化して単位長さにします:$y_i = \frac{U_{i*}}{|U_{i*}|}$
- $U_{i*}$ は $U$ の $i$ 行目
- 正規化されたデータポイント $y_i \in \mathbb{R}^k$ に k-means を適用して最終的なクラスタを得ます
スペクトラルクラスタリングの直感的理解
スペクトラルクラスタリングが持つ性能を直感的に理解するためには、グラフカットの観点から考えると良いです。
グラフカットとは?
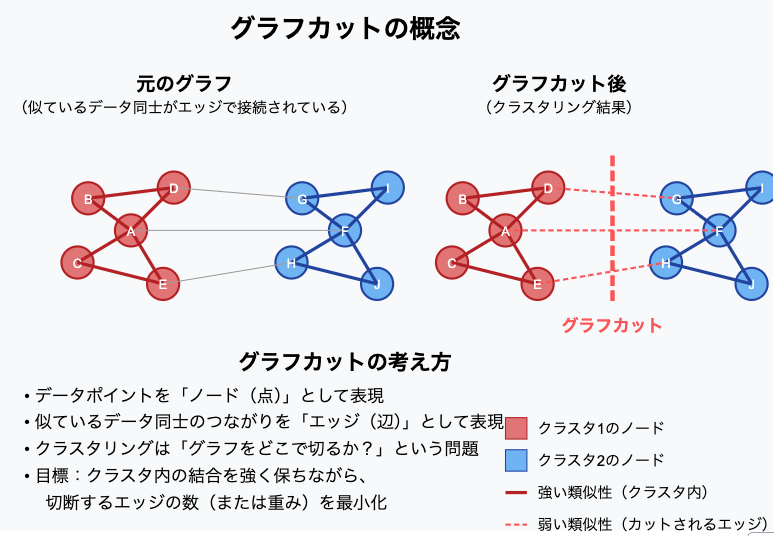
データをグラフ(ネットワークのような構造)として考え、
データをつなぐ「辺(リンク)」をなるべく少なくしながら分割 する方法を探すのが グラフカット です。
たとえば、次のようなケースを考えます
- 各データポイントを「ノード(点)」
- 似ているデータ同士のつながりを「辺(リンク)」
として表すと、クラスタリングは 「グラフをどこで切るか?」 という問題になります。
最小カット問題とその課題
で、グラフを分ける際、単純に「つながりの少ないところで切る(最小カット)」という方法を考えていきます。
しかし、単純な最小カットには以下のような問題があります
- 極端な分割が起きる
- たとえば、一つのノードだけを孤立させるようなカットが最小になる場合がある。
- バランスが取れない
- 一方のクラスタが極端に小さくなり、適切なクラスタリングができない。
この問題を解決するために、スペクトラルクラスタリングでは、「正規化カット(Normalized Cut)」や「比率カット(Ratio Cut)」 という基準を最適化する方法が使われます。
- 正規化カット(Ncut)
クラスタ内のつながりの強さも考慮しながらカットする方法。
極端な分割を防ぎ、バランスの取れたクラスタリングが可能。 - 比率カット(Ratio Cut)
各クラスタのサイズ(ノード数)も考慮して分割を行う方法。

で上記のグラフカットの最適化問題は、 ラプラシアン行列の固有ベクトルを求めること によって解決できるという訳です。
- ラプラシアン行列の固有ベクトルは、「最適なカットの仕方を示す指標」 に。
- 固有ベクトルを使うことで、クラスタリング問題を「連続的な近似解」として解ける。
他手法と比較したメリット
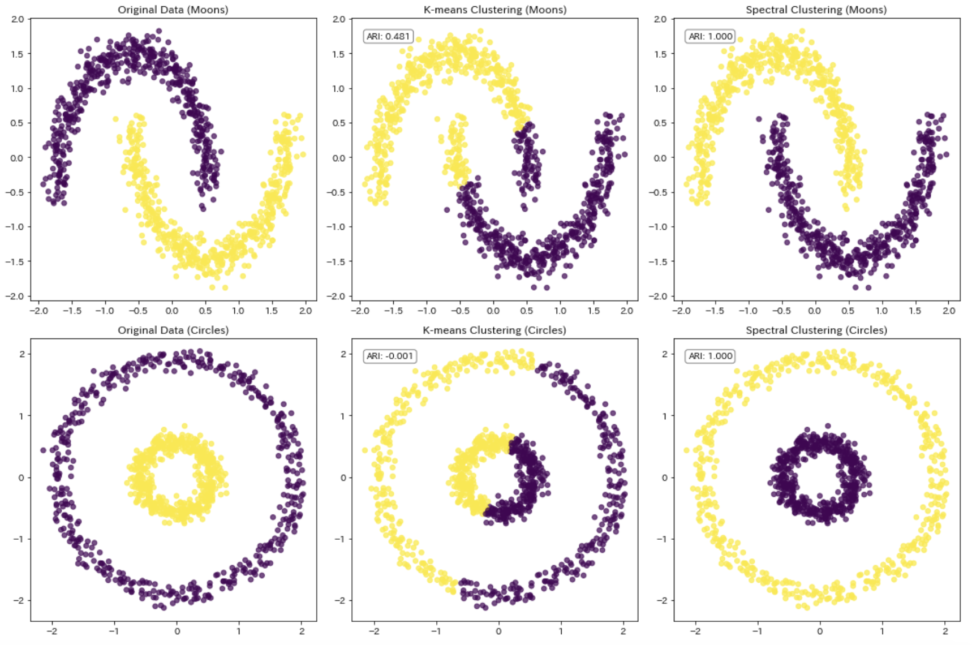
複雑な形状のクラスタでも効果的に分離できる。従来のk-meansが球状クラスタにのみ効果的なのに対し、スペクトラルクラスタリングは非凸な形状のクラスタも適切に識別できます。
スペクトラルクラスタリングのアルゴリズム詳細
スペクトラルクラスタリングのアルゴリズムを段階的に詳しく説明します
入力
- データポイント
- $x_1, x_2, …, x_n$
- クラスタ数
- $k$
- 類似度関数(例:ガウシアンカーネル)とそのパラメータ
手順
さて、手順をおさらいしましょう。
類似度行列の構築
まず、データポイント同士の「似ている度合い(類似度)」を計算します。
これをすべてのデータ点の組み合わせについて計算し、$n \times n$ の 類似度行列 $W$ を作成します。
- 類似度の測り方には、ガウスカーネル(RBFカーネル) や k近傍グラフ などがありました。
- 例えば、ガウスカーネルを使うと、
- ${W_{ij} = \exp\left(-\frac{\|x_i – x_j\|^2}{2\sigma^2}\right) }$
- これは、データ点 $x_i$ と $x_j$ の距離が小さいほど、大きな値になります。
ラプラシアン行列の計算
類似度行列 $W$ から、データの構造を表す ラプラシアン行列 を作ります。
(1) 次数行列 $D$ を計算
次数行列 $D$ は、類似度行列の各行の合計を対角成分にもつ対角行列です。
$${D_{ii} = \sum_j W_{ij}}$$

(2) ラプラシアン行列 $L$ を計算
つまり、各データポイントがどれだけ他のデータとつながっているかを表します。
ラプラシアン行列には、主に2つの種類があります。
- 非正規化ラプラシアン
- ${L = D – W}$
- 基本的なラプラシアン行列で、グラフの構造をそのまま反映します。
- 正規化ラプラシアン
- ${L_{sym} = I – D^{-1/2} W D^{-1/2}}$
- こちらはデータポイントの影響を均一にするため、次数行列を使って正規化したもの
固有値分解
ラプラシアン行列の 固有値と固有ベクトル を計算します。
- 固有値分解を行い、小さい方から $k$ 個の固有値 に対応する固有ベクトルを取得します。
- これにより、データの構造を低次元空間に埋め込みます。
低次元表現
選んだ $k$ 個の固有ベクトルを 行列 $U \in \mathbb{R}^{n \times k}$ に並べます。
- 各データポイントは、$U$ の各行に対応する $k$ 次元のベクトルとして表されます。
- 必要なら、$U$ の各行を単位ベクトルに正規化することもあります。
クラスタリング
最後に、新しく得られた $k$ 次元空間でクラスタリングを行います。
- $U$ の各行(データの新しい表現)に対して、k-meansクラスタリング を適用します。
- これにより、各データポイントにクラスタラベルが割り当てられます。
計算量
スペクトラルクラスタリングの計算量は主に2つの部分から成ります:
- 類似度行列の構築:$O(n^2d)$($n$ はデータポイント数、$d$ は特徴次元数)
- 固有値分解:一般的に $O(n^3)$、ただし疎行列の場合はより効率的なアルゴリズムを使用可能
大規模なデータセットに対しては、近似アルゴリズムやニスチン法、ランダムサンプリングなどの手法を用いて計算を効率化することがあります[青の統計学の「大規模データの次元削減手法」へのリンク]。
Pythonによる実装
それでは、Pythonを使用してスペクトラルクラスタリングを実装し、視覚化してみましょう。
scikit-learnのmake_moonsとmake_circles関数を使用して、線形分離が困難な2つのデータセットを生成しています。

単純にkmeansだけでは、うまく分類はできないデータです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons, make_circles
from sklearn.cluster import KMeans, SpectralClustering
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import adjusted_rand_score
# 非線形データを生成
n_samples = 1000
# 半月形のデータセット
X_moons, y_moons = make_moons(n_samples=n_samples, noise=0.08, random_state=42)
# 同心円のデータセット
X_circles, y_circles = make_circles(n_samples=n_samples, noise=0.05, factor=0.3, random_state=42)
# データの標準化
scaler = StandardScaler()
X_moons_scaled = scaler.fit_transform(X_moons)
X_circles_scaled = scaler.fit_transform(X_circles)
# プロット設定
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
titles = ['Original Data', 'K-means Clustering', 'Spectral Clustering']
# 半月形データセットの処理
axes[0, 0].scatter(X_moons_scaled[:, 0], X_moons_scaled[:, 1], c=y_moons, cmap='viridis', s=30, alpha=0.7)
axes[0, 0].set_title(f"{titles[0]} (Moons)")
# 同心円データセットの処理
axes[1, 0].scatter(X_circles_scaled[:, 0], X_circles_scaled[:, 1], c=y_circles, cmap='viridis', s=30, alpha=0.7)
axes[1, 0].set_title(f"{titles[0]} (Circles)")
# K-meansとスペクトラルクラスタリングを実行
for i, dataset in enumerate([(X_moons_scaled, y_moons, "Moons"), (X_circles_scaled, y_circles, "Circles")]):
X, y_true, dataset_name = dataset
# K-meansクラスタリング
kmeans = KMeans(n_clusters=2, random_state=42)
y_pred_kmeans = kmeans.fit_predict(X)
axes[i, 1].scatter(X[:, 0], X[:, 1], c=y_pred_kmeans, cmap='viridis', s=30, alpha=0.7)
axes[i, 1].set_title(f"{titles[1]} ({dataset_name})")
kmeans_score = adjusted_rand_score(y_true, y_pred_kmeans)
axes[i, 1].text(0.05, 0.95, f"ARI: {kmeans_score:.3f}", transform=axes[i, 1].transAxes,
verticalalignment='top', bbox=dict(boxstyle='round', facecolor='white', alpha=0.5))
# スペクトラルクラスタリング
spectral = SpectralClustering(n_clusters=2, eigen_solver='arpack',
affinity='nearest_neighbors', n_neighbors=10, random_state=42)
y_pred_spectral = spectral.fit_predict(X)
axes[i, 2].scatter(X[:, 0], X[:, 1], c=y_pred_spectral, cmap='viridis', s=30, alpha=0.7)
axes[i, 2].set_title(f"{titles[2]} ({dataset_name})")
spectral_score = adjusted_rand_score(y_true, y_pred_spectral)
axes[i, 2].text(0.05, 0.95, f"ARI: {spectral_score:.3f}", transform=axes[i, 2].transAxes,
verticalalignment='top', bbox=dict(boxstyle='round', facecolor='white', alpha=0.5))
plt.tight_layout()
plt.show()