グラフニューラルネットワークの基礎と応用事例

1. はじめに

我々の周囲に存在するデータは、必ずしも「画像 (2次元格子)」や「テキスト (系列構造)」のように整然としているわけではありません。ソーシャルネットワークや分子構造、交通ネットワークなど、多くの情報は「ノード (頂点)」と「エッジ (辺)」からなるグラフ構造で表されます。こうした複雑な構造を持つデータを取り扱うために登場したのが、グラフニューラルネットワーク (GNN) です。

GNNは、グラフ構造そのものをニューラルネットワークで直接扱うという点が特徴であり、ソーシャルネットワーク分析、創薬、推薦システムなど幅広い分野で注目を集めています。

早速見ていきましょう。

2. グラフニューラルネットワークとは

2.1. グラフデータとは

グラフは一般的に、${G = (V, E)}$ という形で表現されます。

• ${V}$ はノード (頂点) の集合
• ${E}$ はエッジ (辺) の集合

例えばソーシャルネットワークであれば、ユーザーをノード、ユーザー同士の「友達関係」をエッジと考えられます。化学分野では、原子をノード、化学結合をエッジとみなすことで分子構造を表現できます。

従来のニューラルネットワーク (CNNやRNNなど) は画像やテキストといった「格子」や「系列」構造を扱うのに特化しており、グラフのように可変長かつ不規則な構造を持つデータを直接取り扱うのは困難でした。そこで、ノード間の繋がり (隣接関係) をうまく活用しつつ学習を行うフレームワークとしてGNNが登場しました。

2.2. GNNの基本的な考え

GNNでは、各ノードが隣接ノードの情報を集約 (aggregation) する形で特徴量を更新していきます。このとき、エッジ (ノード間の関係性) がその結合の強さや種類などを反映できるような重みづけを担うこともあります。

隣接ノードの情報を繰り返し取り込み、ノードの表現を徐々に「高次の表現」にしていくのがGNNの根本的な仕組みです。

3. 主要なGNNモデルと特徴

GNNには多種多様なモデルが提案されてきましたが、ここでは代表的な3モデル (GCN, GraphSAGE, GAT) と、それ以外のGNNモデルおよび空間的手法 (Spatial GNN) の課題についてご紹介します。

3.1. GCN (Graph Convolutional Network)

GCNは、グラフにおける「畳み込み (Convolution)」という概念を初めて本格的に導入した初期モデルの一つです。基本アイデアは「隣接ノードの特徴量を正規化したうえで集約する」ことにあり、数式は以下のように表されます。

$${H^{(l+1)} = \sigma\bigl(\tilde{D}^{-\frac{1}{2}} \tilde{A}\,\tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)}\bigr)}$$

• ${H^{(l)}}$: ${l}$ 層目のノード特徴量行列
• ${\tilde{A} = A + I}$: 隣接行列 ${A}$ に単位行列 ${I}$ を加えたもの (自己ループの追加)
• ${\tilde{D}: \tilde{A}}$の対角要素を次数とする次数行列
• ${W^{(l)}}$: ${l}$ 層目のパラメータ (重み行列)
• ${\sigma}$: 活性化関数 (ReLUなど)

シンプルでありながら多くの場面で良好な性能を示し、後続のモデルに強い影響を与えました。ただし、有向グラフへの対応が難しいことや、深い層にすると過平滑化が起こりやすいなどの弱点があります。

3.2. GraphSAGE

GraphSAGEは、GCNを大規模グラフに適用しやすいように拡張したモデルです。全ての隣接ノードの特徴量を集約すると計算量が膨れあがるため、ノードの隣接ノードをサンプリングして特徴量を集約します。さらに、学習済みの集約関数を用いることで未知のノードに対しても推論ができる（帰納的学習）という利点があります。

• GCN: 隣接ノード全てを対象に計算 ⇒ トランスダクティブ (学習データに存在しないノードは予測不可)
• GraphSAGE: 隣接ノードをサンプリング ⇒ 帰納的 (学習データにないノードでも特徴量がわかれば予測可能)

3.3. GAT (Graph Attention Network)

GATは、アテンション機構 (Self-Attention) を用いて各ノードの隣接ノードの重要度を学習的に決定します。

すなわち、ノード ${i}$ とノード ${j}$ の特徴量の類似度などに基づいて「重み (${\alpha_{ij}}$)」を求め、

$${h_i^{(l+1)} = \sigma\Bigl(\sum_{j \in N(i)\cup \{i\}} \alpha_{ij}^{(l)}\, W^{(l)}\Bigl)}$$

のようにノード ${i}$ の表現を更新します。ここで ${\alpha_{ij}^{(l)}}$ は、アテンションスコアをsoftmaxなどで正規化したものです。

これにより、重要度が高い隣接ノードの情報を強く取り込み、そうでないノードの影響は抑えることができます。

3.4. その他のGNNモデルとSpatial GNNの課題

• グラフオートエンコーダ (GAE/VGAE): ノード埋め込みを学習し、グラフ構造を再構築することで次元圧縮やリンク予測を実現。
• 空間-時間GNN (STGNN): 時系列付きグラフを扱うために、空間情報 + 時間情報を同時にモデル化。

一方で、Spatial GNN には以下のような課題が指摘されています。

4. グラフ畳み込みの数学的基礎

GNNにおける「畳み込み」は、画像のような2次元格子におけるフィルタ操作とは異なり、グラフ構造上で「ノード + 隣接関係」を考慮した演算を指します。代表的な定義としてはスペクトル的手法と空間的手法があります。

4.1. スペクトル的手法

スペクトル的手法では、グラフラプラシアン${L = D – A}$ (もしくは正規化ラプラシアン ${\tilde{L} = I – D^{-1/2} A D^{-1/2}}$) の固有ベクトルを使ったグラフフーリエ変換を定義し、周波数領域上でのフィルタ操作としてグラフ畳み込みを定義します。

• グラフフーリエ変換
  • ${\hat{x} = U^T x }$
    • ${U}$ はラプラシアンの固有ベクトルを列に持つ行列
• フィルタ演算
  • ${\hat{y} = g_\theta(\Lambda)\hat{x}}$
    • ${\Lambda}$ はラプラシアンの固有値対角行列

しかし、固有分解の計算コストが高く、大規模グラフには不向きであることなどから、よりローカルな空間的手法が注目されるようになりました。

4.2. 空間的手法

空間的手法では、ノード ${i}$ の特徴量更新を「ノード ${i}$ とその近傍ノード ${j \in N(i)}$ の特徴量を集約する」形で定義します。

たとえば、GCNで登場した式 (自己ループ込み) はその典型例です。

4.3. GCNにおける数式の詳細

GCNの1層分の更新式をもう少しローカルな形で書くと、以下のように表せます。

$${h_i^{(l+1)} = \sigma\Bigl( \sum_{j \in N(i) \cup \{i\}} \frac{1}{\sqrt{d_i d_j}} \, W^{(l)}\, h_j^{(l)} \Bigr)}$$

• ${h_i^{(l)}}$​: ${l}$層目のノード ${i}$ の特徴ベクトル
• ${N(i)}$: ノード ${i}$の隣接ノード集合
• ${d_i}$​: ノード ${i}$の次数
• ${W^{(l)}}$: 学習パラメータ行列
• ${\sigma}$: 活性化関数

ノード ${i}$ の次数 ${d_i}$​ とノード ${j}$ の次数 ${d_j}$​ を使って、重みを正規化しています。

この正規化により、大きい次数を持つノード (多くの隣接先を持つノード) の情報が過大に影響を受けないように調整しています。

5. GNNの応用分野「薬物発見における分子特性予測」

今日は、GNNを利用している論文を紹介します。

Could graph neural networks learn better molecular representation for drug discovery? A comparison study of descriptor-based and graph-based models

5.1. 研究背景

医薬品開発では、候補となる化合物が薬として体内でどのように振る舞うかを予測することは創薬の観点で大事です。これは、薬がどのように吸収され、体内にどのように分布し、どのように代謝され、どのように排泄され、そして毒性があるかどうかを予測することを意味します。これらの特性をまとめて ADME/T と呼びます。

ADME/T 特性を予測することで、薬が効果的に作用するかどうか、副作用があるかどうかを早期に評価することができます。この予測は、創薬プロセス全体を効率化し、より安全で効果的な医薬品の開発に役立ちます。

簡単に言うと、薬の候補が体内でどのように働くかを予測して、良い薬かどうかを判断するということです。

で、従来、このタスクには、サポートベクターマシン（SVM）、ランダムフォレスト（RF）、ディープニューラルネットワーク（DNN）などの機械学習（ML）法が広く使用されてきました。

というか、分子はどうデータ化できるのか？

分子は一連の原子（ノード）と一連の結合（エッジ）で構成されるグラフと見なすこともできます。

本質的に、GNNは、分子グラフ全体にメッセージを渡すことによって、原子特徴ベクトルによってエンコードされた隣接原子からの情報と、結合特徴ベクトルによってエンコードされた接続された結合の情報を集約することによって、各原子の表現を学習することを目的としています

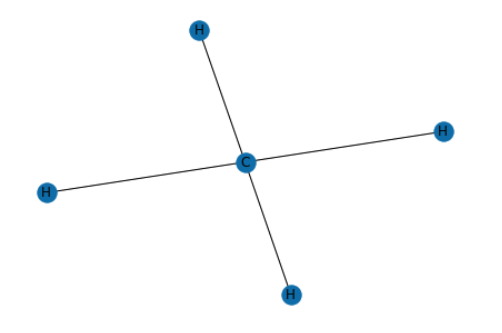
メタン（CH4）分子をグラフ構造で表現しています。

• 各原子はノードとして表現しています
• 原子間の結合はエッジとして表現されています。

5.2. やったこと

近年、グラフニューラルネットワーク（GNN）が分子特性予測のためのモデリング手法として注目されています。GNN は、分子グラフの構造情報を活用して、分子の特性を予測します。多くの研究において、GNN は従来の記述子ベースの手法よりも優れた結果を出すことが示されているようですね。

しかし、GNN が従来の記述子ベースの手法よりも優れているという結論は依然として議論の余地があります。そこで、この研究では、さまざまな特性エンドポイントをカバーする 11の公開データセットを用いて、記述子ベースのモデルとグラフベースのモデルの予測能力と計算効率を幅広くテストし、比較したようです。

GATは、上述した通りグラフ畳み込みネットワーク（GCN）を拡張したもので、異なるノードに異なる重みを指定することによるattentionメカニズムが導入され、対応するグラフ畳み込み演算は、次の式で隣接情報の加重合計を集約します。

$${H(l+1)i = \sigma ( \sum{j∈N(i)} \alpha(l)_{ij}W(l)H(l)_i)}$$

• $α(l)_{ij}$ は、$l$番目のグラフ畳み込み層におけるノード $i$ とノード $j$ 間の正規化されたattentionスコア
• $W$:学習可能な重み行列
• $N(i)$:ノード $i$ が情報を受け取る対象となる隣接ノードの集合を
• $\sigma$ は非線形活性化関数

で、GATは、ClinToxデータセットにおいて、他のモデルよりも優れた予測精度を示しましたが、他のデータセットでは、SVM、XGBoost、RFなどの記述子ベースのモデル、あるいは他のグラフベースモデルの方が優れた予測精度を示しました。

計算効率の点では、GATは、GCNよりも計算コストが高く他モデルよりもはるかに計算コストが高いことがわかりました。

6. 学習プロセスと損失関数

GNNの学習プロセスは、他のニューラルネットワーク同様に順伝播 → 損失計算 → 逆伝播 → パラメータ更新を繰り返す形で行われます。タスクに応じて以下のような損失関数が用いられます。

• ノード分類: クロスエントロピー損失 (ソフトマックス出力との誤差)
• グラフ分類: グラフプーリングやReadoutで得たグラフ全体の表現に対する分類損失
• リンク予測: 2値分類損失 (エッジの有無) やスコアリング関数の回帰損失 など

7. PyTorch Geometric を用いたサンプル実装

ここでは、PyTorch Geometric を使ったGCNによるノード分類のサンプルコードを省略せず提示します。

サンプルとして、Coraデータセット (論文引用ネットワーク) を用いた学習例を示します。

import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
from torch_geometric.datasets import Planetoid

# 1. データセットの読み込み (Coraを例に)
dataset = Planetoid(root='data/Cora', name='Cora')
data = dataset[0]

# 2. GCNモデルの定義
class GCNNet(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels, out_channels):
        super(GCNNet, self).__init__()
        self.conv1 = GCNConv(in_channels, hidden_channels)
        self.conv2 = GCNConv(hidden_channels, out_channels)
    
    def forward(self, x, edge_index):
        # 1層目
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        # 2層目
        x = self.conv2(x, edge_index)
        return x

# 3. モデル・最適化手法の設定
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = GCNNet(in_channels=dataset.num_node_features,
               hidden_channels=16,
               out_channels=dataset.num_classes).to(device)
data = data.to(device)

optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)

# 4. 学習ループ
def train():
    model.train()
    optimizer.zero_grad()
    out = model(data.x, data.edge_index)
    loss = F.cross_entropy(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()
    return loss.item()

@torch.no_grad()
def test():
    model.eval()
    out = model(data.x, data.edge_index)
    preds = out.argmax(dim=1)
    
    accs = []
    for mask in [data.train_mask, data.val_mask, data.test_mask]:
        correct = preds[mask].eq(data.y[mask]).sum().item()
        accs.append(correct / mask.sum().item())
    return accs  # [train_acc, val_acc, test_acc]

for epoch in range(1, 201):
    loss = train()
    train_acc, val_acc, test_acc = test()
    if epoch % 20 == 0:
        print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}, '
              f'Train Acc: {train_acc:.4f}, '
              f'Val Acc: {val_acc:.4f}, '
              f'Test Acc: {test_acc:.4f}')

解説

1. Planetoid (Cora, CiteSeer, PubMed) などの定番データセットをロード。
2. GCNConv というPyTorch Geometricのレイヤーを2層用い、隠れ層 (hidden_channels) と出力層 (out_channels) を構成。
3. 学習ではクロスエントロピー損失を用い、train/val/testのマスクを使って精度を算出。
4. 学習を200エポック繰り返し、精度を確認。

このようにPyTorch Geometricを用いることで、グラフ構造を意識したニューラルネットワークを非常に簡単に記述できるのがポイントです。

×

FOLLOW ME ！

@blue_statistics