活性化関数の完全ガイド|特徴と効果的な選び方について|ニューラルネットワークと非線形性
こんにちは、青の統計学です。
今回は、深層学習でもお馴染みの活性化関数についてまとめて理解するための記事を書きました。
活性化関数とは、ニューラルネットワークの各ニューロン(ノード)が、前の層から受け取った入力の重み付き和(線形結合)を、次の層へ渡す前に適用する非線形な変換のことですが、種類があるので一つずつ特徴やメリットデメリットを確認していきましょう。
線形結合の限界:多層にしても単層と変わらない数学的理由
ニューラルネットワークの仕組みはある程度知識があるものとして進めます。
さて、活性化関数がない場合、ニューラルネットワークは単なる線形変換の繰り返しになってしまいます。例えば、ある層の出力を$y = W_1 x + b_1$とし、次の層の出力を$z = W_2 y + b_2$とします。ここに$y$を代入すると、次のようになります。
$$z = W_2 (W_1 x + b_1) + b_2$$
これを展開すると、
$$z = (W_2 W_1) x + (W_2 b_1 + b_2)$$
となります。
ここで、新しい行列$W’ = W_2 W_1$と新しいベクトル$b’ = W_2 b_1 + b_2$を定義すれば、
$$z = W’ x + b’$$
という、たった一つの線形変換として表現できてしまいます。

つまり、活性化関数を挟まなければ、層をいくら深くしても、表現できるのは単層の線形モデルと数学的に全く同じなのです。
活性化関数の役割について
この線形性のデメリットを克服して、ニューラルネットワークに複雑なパターンを学習する能力を与えるのが、活性化関数というわけです。
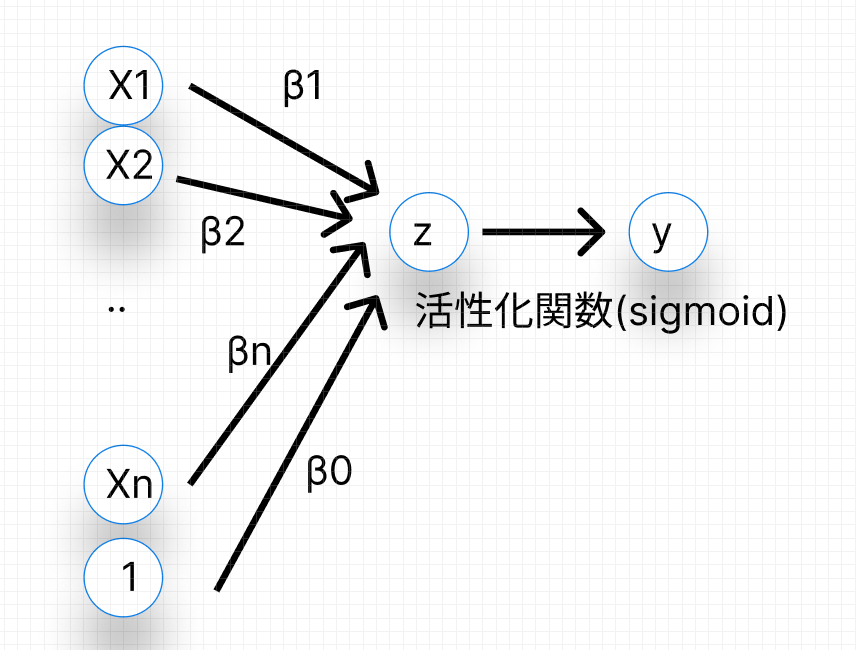
活性化関数は、入力に対して非線形な操作を加えることで、ネットワーク全体を非線形モデルへとかえます
あんまり関係がないですが、この非線形変換は、統計学で学ぶ一般化線形モデル(Generalized Linear Model, GLM)におけるリンク関数の役割と似ていると思います。
GLMでは、線形予測子を目的変数の期待値に結びつけるためにリンク関数を用いますが、ニューラルネットワークでは、線形結合の結果を次の層の入力として「活性化」させるために活性化関数を用います。

この「活性化」とは、「この情報(入力)は重要だから次の層に渡す」「この情報は重要でないから抑制する」という、一種の情報の取捨選択を意味します。
活性化関数とその数学的背景
代表的な活性化関数を見ていきましょう。
シグモイド関数(Sigmoid Function)
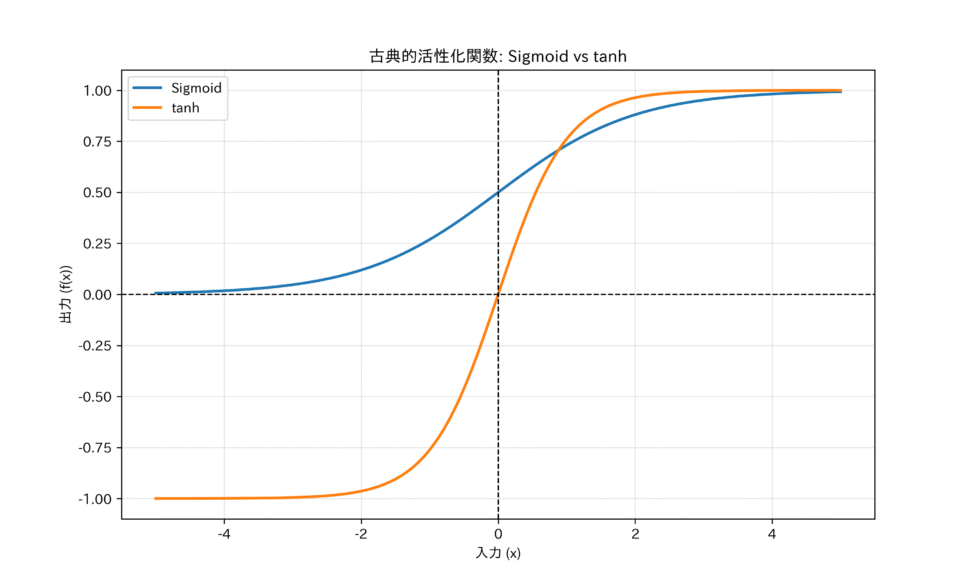
シグモイド関数は、任意の入力値を0から1の範囲に押し込める(スケーリングする)特徴を持ちます。
数学的定義
$$f(x) = \frac{1}{1 + e^{-x}}$$
シグモイド関数は、ロジスティック回帰で用いられる関数そのものであり、出力を確率として解釈できる点が大きな利点でした。つまり、ニューロンの出力が「次の層に情報を渡す確率」や「あるクラスに属する確率」として直感的に理解できるのです。
統計学で学ぶベルヌーイ分布のパラメータ(成功確率$p$)を推定する際に、線形予測子を確率に変換する役割を果たします。
ベルヌーイ分布の基本を徹底解説!期待値・分散の計算方法とは?
課題:勾配消失問題について
しかし、シグモイド関数には、勾配消失問題という課題がありました。
この問題は、その導関数(微分)の形を見れば明らかになります。
シグモイド関数の導関数は、
$$f'(x) = f(x) (1 – f(x))$$
となります。(G検定とかでもよく問われる話です。)
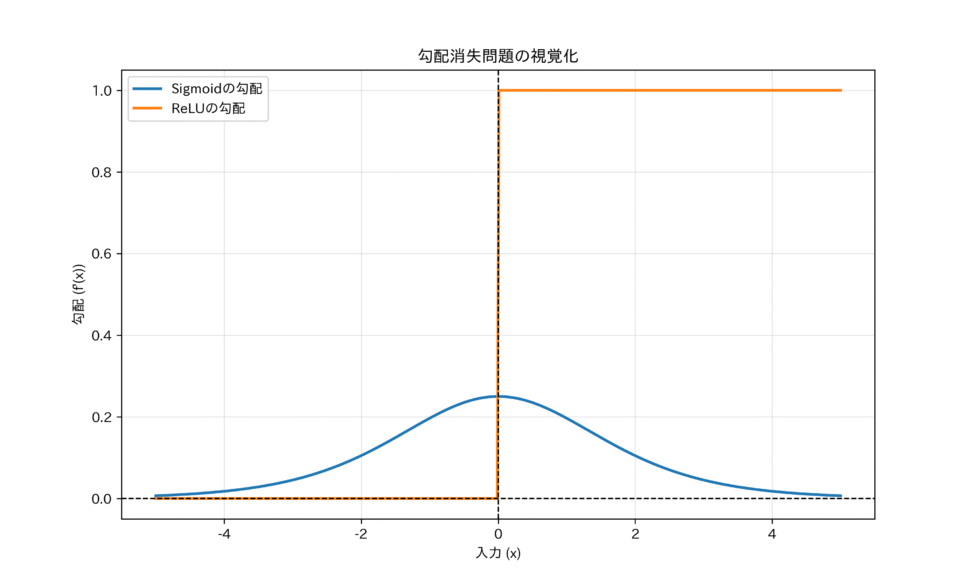
この導関数の最大値は、入力$x=0$のとき、すなわち$f(x)=0.5$のときに0.25です。
$${\max(f'(x)) = 0.5 \times (1 – 0.5) = 0.25}$$
ニューラルネットワークの学習は、誤差逆伝播法(Backpropagation)によって行われますが、これは勾配(微分値)を層ごとに掛け算しながら後方へ伝えていくプロセスです。もし勾配が常に0.25以下であれば、層を深くする(例えば10層)につれて、勾配は$0.25^{10}$というように指数関数的に小さくなっていきます。
$$0.25^{10} \approx 0.00000095$$
双曲線正接関数(tanh Function)
シグモイド関数の課題を改善するために登場したのが、双曲線正接関数(ハイパボリックタンジェント)です。
数学的定義
$$f(x) = \tanh(x) = \frac{e^x – e^{-x}}{e^x + e^{-x}}$$
この関数は、シグモイド関数と線形変換で結びついています。
$$\tanh(x) = 2 \cdot \text{sigmoid}(2x) – 1$$
tanh関数の出力範囲は-1から1です。このゼロ中心であるという特性が、学習効率の向上に寄与します。シグモイド関数は出力が常に正(0から1)であるため、勾配も常に同じ符号(正)になり、重みの更新方向が偏ってしまうという問題がありましたが、tanhは正負の出力を持つため、この問題は緩和されました

しかし、tanh関数も入力の絶対値が大きくなると勾配がゼロに近づくため勾配消失問題自体は解決できませんでした。
勾配と勾配消失問題について深掘り
もう少し、掘り下げてみましょう。簡単に説明すると、勾配とは「損失関数の傾き」です。で損失関数とは、モデルと正解(教師データ)の差を表す関数ですね。線形代数の文脈で言えば、勾配は損失関数の微分によって得られるベクトルです。勾配は、各パラメータ(重みとバイアス)に対する損失関数の偏微分から構成されます。
$$∇L = (\frac{∂L}{∂_{w1}}, \frac{∂L}{∂_{w2}}, …, \frac{∂L}{∂_{wn}})$$
ここで、\(\frac{∂L}{∂w_i}\) は損失関数 L に対するパラメータ \(wi\) の偏微分です。損失関数が \(L(w1, w2, …, wn\) で表される場合、勾配は各パラメータに対する損失関数の偏微分から構成されるベクトルです。)
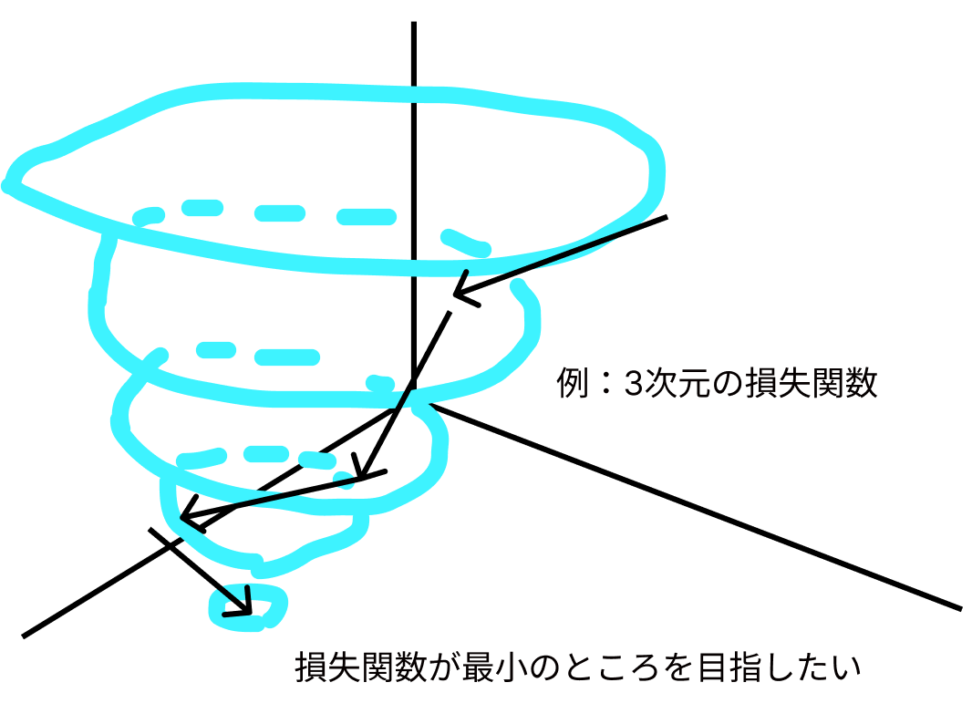
勾配が示す方向は、損失関数の値が最も急速に増加する方向です。
機械学習では、「最急勾配降下法」という手法が主流で、文字通り勾配が最も大きい方の逆(超大事)に進んで損失関数をどんどん小さくしていきます。そして最適なパラメータは、損失関数を最小化するパラメータということです。
以下のように勾配を更新し、損失関数を小さくしていきます。
$$w_{new} = w_{old} – α × ∇L$$
- w_old: 更新前のパラメータ
- w_new: 更新後のパラメータ
- α: 学習率(ステップサイズ)
- ∇L: 損失関数 L に対する勾配
損失関数には、「勾配が最大のところにどれくらい進むか」を設定する「学習率α」というパラメータがあり、学習率が小さすぎるといつまで経っても学習が終わらないなどの弊害があったります。逆に学習率が大きすぎると、損失関数の最小値を通り過ぎて発散してしまします。
これを勾配爆発と呼びます。
で、勾配消失問題は、ディープニューラルネットワークにおいて、誤差逆伝播時に勾配が急速に小さくなり、最適化が困難になる現象です。
これは、ニューラルネットワークの学習が遅くなったり、停滞したりする原因となります。勾配消失問題は、主に活性化関数とネットワークの深さに関連しています。
先ほども言及した通りで、Sigmoid関数やTanh関数では、入力の絶対値が大きい場合に勾配が極端に小さくなります。
シグモイド関数
$$f(x) = \frac{1}{1 + exp(-x)}$$
\(f'(x) = f(x) * (1 – f(x))\)より、この導関数(微分係数)の最大値は0.25です。Tahn関数
$$f(x) = \frac{exp(x) – exp(-x))}{(exp(x) + exp(-x)}$$
\(f'(x) = 1 – f(x)^2\)より、この導関数(微分係数)の最大値は1です。
これらの活性化関数では、入力が 0 から離れるにつれて導関数の値が急速に 0 に近づきます。誤差逆伝播時に、勾配が連続的にこれらの導関数によって乗算されるため、ネットワークが深いほど勾配が指数関数的に小さくなります。これが勾配消失問題の原因です
ReLUとその系譜
続いては、よく使われるシンプルな活性化関数、ReLU(Rectified Linear Unit)の登場です。
ReLUは、その単純さにもかかわらず、勾配消失問題を劇的に改善し、ディープラーニングの標準となりました。
数学的定義
$$f(x) = \max(0, x)$$
ReLUの導関数(微分)は、
$$f'(x) = \begin{cases} 1 & (x > 0) \\ 0 & (x \le 0) \end{cases}$$
となります。
入力$x$が正の領域では、勾配は常に1です。勾配が1であれば、誤差逆伝播の際に勾配が減衰することなく、そのまま次の層へ伝わります。

つまり、勾配消失問題が原理的に発生しないのです。
また、ReLUは$x \le 0$の領域では出力が0となるため、ニューロンの約半分を不活性化させます。これはスパース性をネットワークに導入し、モデルの表現力を高めつつ、計算効率も向上させます。
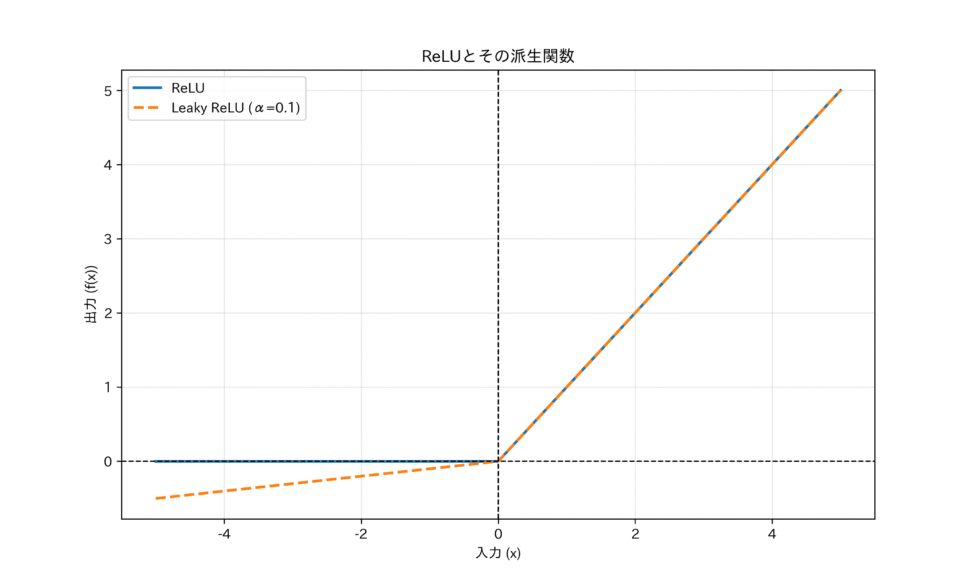
課題:Dying ReLU
ReLUにも課題があります。それはDying ReLU現象です。
学習中に大きな勾配が流れると、重みが大きく更新され、あるニューロンへの入力が常に負になってしまうことがあります。一度入力が負になると、そのニューロンの出力は常に0、勾配も常に0になります。勾配が0になると、そのニューロンは二度と重みを更新できなくなり、ネットワークから永久に切り離された状態になってしまいます。
Leaky ReLU と Parametric ReLU (PReLU)
Dying ReLU現象を克服するために提案されたのが、ReLUの負の領域にわずかな傾きを持たせる改良版です。
Leaky ReLUの数学的定義は、
$$f(x) = \begin{cases} x & (x > 0) \\ \alpha x & (x \le 0) \end{cases}$$
$\alpha$は0.01などの非常に小さな固定値です。
Parametric ReLU (PReLU)は、この$\alpha$を固定値ではなく、学習可能なパラメータとして扱うことで、データから最適な傾きを自動で獲得しようとします。
これらの改良は、負の領域でもわずかながら勾配($\alpha$)を保持することで、ニューロンが完全に死ぬことを防ぎ、情報の完全な損失を防ぐという、数学的な情報の流れを途絶えさせないための試みです。
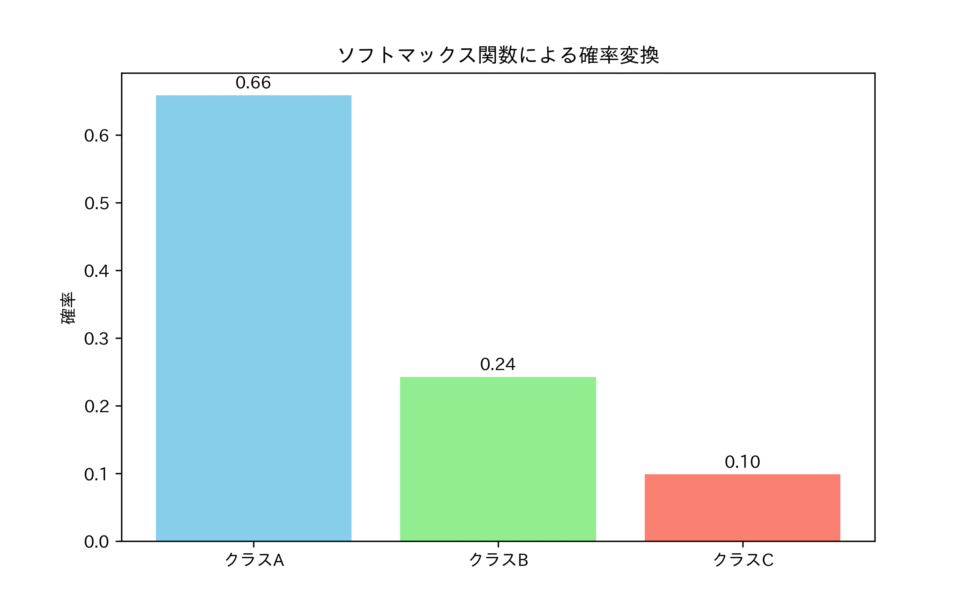
ソフトマックス関数(Softmax Function)
隠れ層で主に非線形性を導入するReLU系関数が使われるのに対し、ネットワークの出力層では、そのタスクの性質に応じた特殊な活性化関数が使われます。分類問題で重要なのがソフトマックス関数です。
【Transformer】ソフトマックス関数についてわかりやすく解説|python
ソフトマックス関数は、複数のニューロンの出力を、総和が1になる確率分布へと変換します。
数学的定義
$$f(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{K} e^{x_j}}$$
ここで、$x_i$は$i$番目のニューロンの入力(ロジット)であり、$K$はクラスの総数です。
この関数が多クラス分類において美しいとされる理由は、その出力が確率の公理(非負性、総和が1)を満たすことに加えて、交差エントロピー誤差(Cross-Entropy Loss)と組み合わせた際の勾配計算の簡便さにあります。
ソフトマックス関数と交差エントロピー誤差を組み合わせた際の勾配は、出力された確率と正解ラベルの差として表現されます。
$$\frac{\partial L}{\partial x_i} = y_i – t_i$$
- $L$は損失関数
- $y_i$はソフトマックスの出力(予測確率)
- $t_i$は正解ラベル
めちゃくちゃシンプルですね!

つまり、「予測と正解のズレ」がそのまま勾配として次の層に伝わるため、非常に効率的かつ直感的な学習が可能になるのです。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!






