【超入門】統計学とは？文系でもわかる『データを武器にする』ための第一歩

こんにちは、青の統計学です。

今回は統計学の基本的な考え方から、それがどのように事象を理解し、変える手助けとなるのかを、数式無しで分かりやすく、そして深く掘り下げていきます。統計学への第一歩を踏み出し、データを味方につけていきましょう。

統計学とは何か？：データの「なぜ？」を解き明かす学問

統計学とは一言で言えば、「データから意味のある情報を引き出し、不確実性の中で合理的な意思決定を行うための学問」です。私たちの周りには、日々、様々なデータが生まれています。例えば、スマートフォンの利用履歴、商品の売上データ、健康診断の結果、天気予報の数値など、挙げればきりがありませんね。

統計学は、これらの「ばらつき」を含むデータから、その背後にある規則性や傾向、あるいは偶然性を明らかにし、未来を予測したり、ある事象の原因を特定したりすることを目指します。

統計学には大きく分けて二つの柱があります。それが「記述統計」と「推測統計」です。

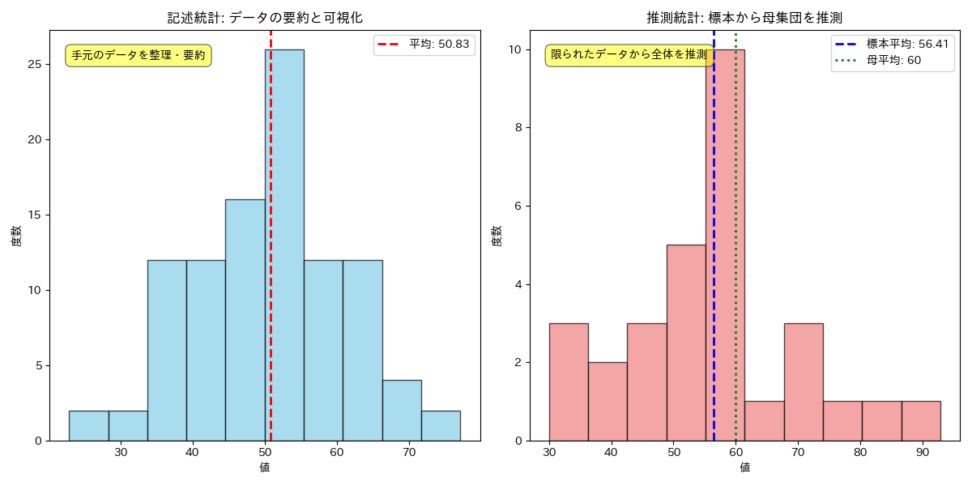
記述統計：データを「要約」し「可視化」する

記述統計は、手元にあるデータを整理し、その特徴を分かりやすく「記述」することに焦点を当てます。例えば、クラスのテストの点数があったとします。これらの点数をただ羅列するだけでは、全体像を把握するのは困難ですよね。

そこで、平均点、最高点、最低点、点数のばらつき具合（分散や標準偏差）などを計算して、要約統計量にして情報量を落としながら、解釈しやすくしたり、ヒストグラムや箱ひげ図などのグラフを使って視覚的に表現したりします。

つまり、記述統計は、膨大なデータをシンプルかつ効果的にまとめるための手法のことです。これにより、データの全体像や傾向を直感的に理解できるようになります。

推測統計：データから「全体」を「推測」する

一方、推測統計は、手元にある限られたデータ（これを「標本」と呼びます）から、まだ見ていない全体（これを「母集団」と呼びます）の性質を推測することを目指します。

例えば、ある新商品の市場での売上を予測したい場合、全国の全消費者にアンケートを取ることは現実的ではありません。そこで、一部の消費者（標本）にアンケートを行い、その結果から全国の消費者（母集団）の購買意欲を推測します。推測統計では、この推測がどれくらい確からしいのか、どれくらいの誤差があるのかを、確率論に基づいて評価します。

そもそも統計学がなぜ必要なのかというと、私たちが直面する多くの問題が、不確実性や変動性を含んでいるからです。統計学は、この不確実性を定量的に捉え、データに基づいた客観的な判断を可能にします。勘や経験だけでなく、データという客観的な根拠に基づいて意思決定を行うことで、より精度の高い予測や、より効果的な戦略立案が可能になります。

統計学の数学的背景：数字の裏にある論理

さて、統計学に興味が湧くように、簡単な用語を紹介します。

統計学は、データを扱う学問である以上、数学と密接な関係にあります。しかし、統計学で使われる数学は、必ずしも複雑な微積分や高度な線形代数ばかりではないです。むしろ、その根幹をなすのは、私たちが日常生活で直感的に理解している「平均」や「ばらつき」といった概念を、厳密に定義し、定量的に扱うためのツールとしての数学です。

ここでは、統計学を理解する上で不可欠な基本的な数学的概念と、確率との関係について解説します。

平均、分散、標準偏差

データの特徴を捉える上で最も基本的なのが、「平均」「分散」「標準偏差」です。

この辺りは、中学や高校での数学でも登場しますね。

平均（Mean）

データの中心的な位置を示す最も一般的な指標です。すべてのデータの値を合計し、データの個数で割ることで求められます。例えば、テストの平均点が高ければ、クラス全体の学力レベルが高いと判断できます。

$${ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i }$$

• $x_i$ は各データ
• $n$ はデータの個数を表します。

分散（Variance）

データの「ばらつき」の度合いを示す指標です。各データが平均からどれくらい離れているかを二乗して合計し、データの個数で割ることで求められます。

なぜ二乗するのかというと、平均より大きい値と小さい値の差が打ち消し合わないようにするためです。分散が大きいほど、データは平均から広範囲に散らばっていることを意味します。

$${ s^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2 }$$

標準偏差（Standard Deviation）

分散の正の平方根を取ったものです。分散は二乗しているため単位が元のデータと異なりますが、標準偏差は元のデータと同じ単位に戻るため、より直感的にばらつきの大きさを理解できます。

例えば、平均点が同じ二つのクラスがあったとしても、標準偏差が小さいクラスは生徒の点数が平均点の周りに集中しているのに対し、標準偏差が大きいクラスは点数のばらつきが大きい、つまり得意な生徒と苦手な生徒の差が大きい、といったことが分かります。

$${ s = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2} }$$

これらの指標は、記述統計においてデータを要約し、その特徴を把握するために不可欠です。そして、これらの概念は、後述する推測統計の基盤ともなります。

確率

統計学、特に推測統計を理解する上で、確率の概念は避けて通れません。確率は、ある事象が起こる「確からしさ」を数値で表すものです。

例えば、サイコロを振って1の目が出る確率は1/6です。これは、何度もサイコロを振れば、およそ6回に1回の割合で1の目が出るだろう、ということを意味します。

統計学では、この確率の考え方を使って、標本から母集団を推測する際の「不確実性」を評価します。例えば、「この標本から得られた結果は、偶然によるものなのか、それとも母集団に本当にそのような傾向があるのか？」という問いに答えるために、確率的な推論を用います。

確率の問題を解いてみたい方はこちらをどうぞ。

確率の基本概念

条件付き確率の基礎

統計学と「大数の法則」

統計学の最も基本的な概念の一つに「大数の法則（Law of Large Numbers）」があります。これは、私たちがデータから全体像を推測する上で、なぜ多くのデータが必要なのか、その根拠を与える法則です。

大数の法則とは？

大数の法則とは、「ある試行を何度も繰り返せば、その結果の平均は、理論的な期待値（真の値）に限りなく近づいていく」という法則です。

例えば、公正なコインを投げた場合、表が出る確率は理論上50%です。しかし、実際にコインを10回投げただけで、ぴったり5回表が出るかというと、そうとは限りませんよね。もしかしたら3回しか出ないかもしれませんし、奇跡的に10回出るかもしれません。

しかし、この試行を100回、1000回、1万回と増やしていくとどうなるでしょうか？表が出る割合は、徐々に50%に近づいていくはずです。これが大数の法則の直感的な意味です。

統計学では、この「試行」を「データの収集」と捉えます。そして、「理論的な期待値」を「母集団の真の値（例えば、母平均）」、「結果の平均」を「標本から計算される平均（標本平均）」と考えます。つまり、大数の法則は、「標本のサイズ（データの数）が大きくなればなるほど、標本から得られる平均値は、母集団の真の平均値に近づいていく」ということを保証してくれるのです。

なぜ大数の法則が重要なのか？

この法則がなぜ統計学において重要なのかでいうと、私たちが現実世界で「母集団の真の値」を直接知ることがほとんど不可能だからです。

例えば、日本人の平均身長を知りたいと思っても、日本に住むすべての人を測定することはできません。そこで、私たちは一部の人々（標本）を抽出し、その標本の平均身長を計算します。この標本平均が、果たして日本人の真の平均身長をどれくらい正確に表しているのか？その問いに答えるのが大数の法則です。

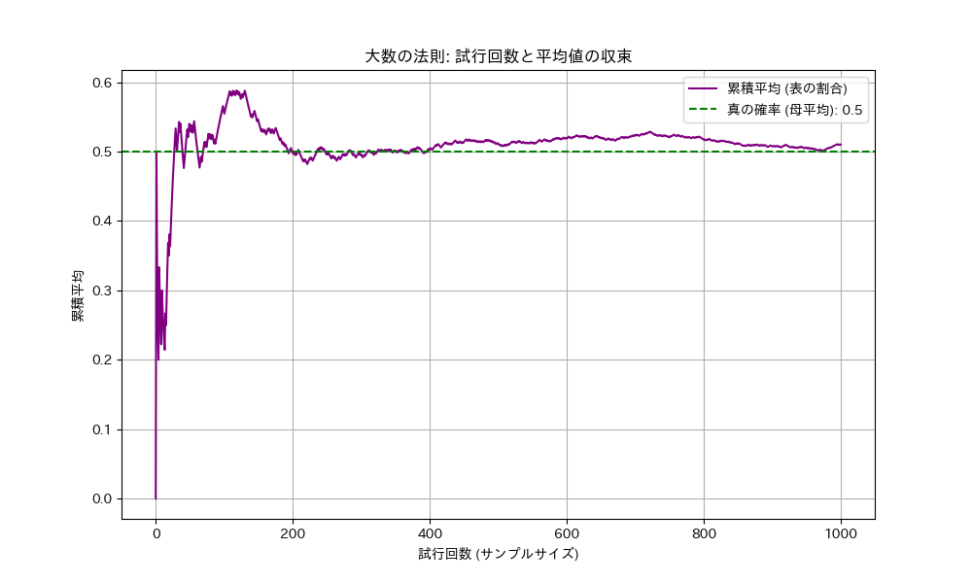
つまり、より多くのデータを集めることで、私たちは母集団の真の姿を、より正確に「推測」できるようになるのです。

仮説検定とは？

統計学の応用の中でも、特にビジネスや研究で頻繁に用いられるのが「仮説検定」です。これは、データに基づいて、ある主張や仮説が正しいかどうかを科学的に判断するための手法です。

仮説検定を理解するために、裁判をイメージしてみましょう。裁判では、まず「被告は無罪である」という仮説（帰無仮説、${H_0}$ と書きます）が立てられます。

そして、検察側は被告が有罪であるという「証拠」を集めます。もし、集められた証拠が「被告が無罪である」という仮説と矛盾するほど強力であれば、その仮説を棄却し、「被告は有罪である」という結論（対立仮説、${H_1}$ と書きます）を採択します。

統計的仮説検定もこれと同じ構造です。

まず、検証したいことと反対の仮説（例えば、「AとBに差はない」）を帰無仮説として設定します。そして、実際にデータを収集し、そのデータが帰無仮説のもとでどれくらい起こりにくいかを評価します。もし、そのデータが帰無仮説のもとでは「ほとんど起こりえない」と判断されるほど珍しいものであれば、帰無仮説を棄却し、対立仮説（例えば、「AとBには差がある」）を採択する、という流れになります。

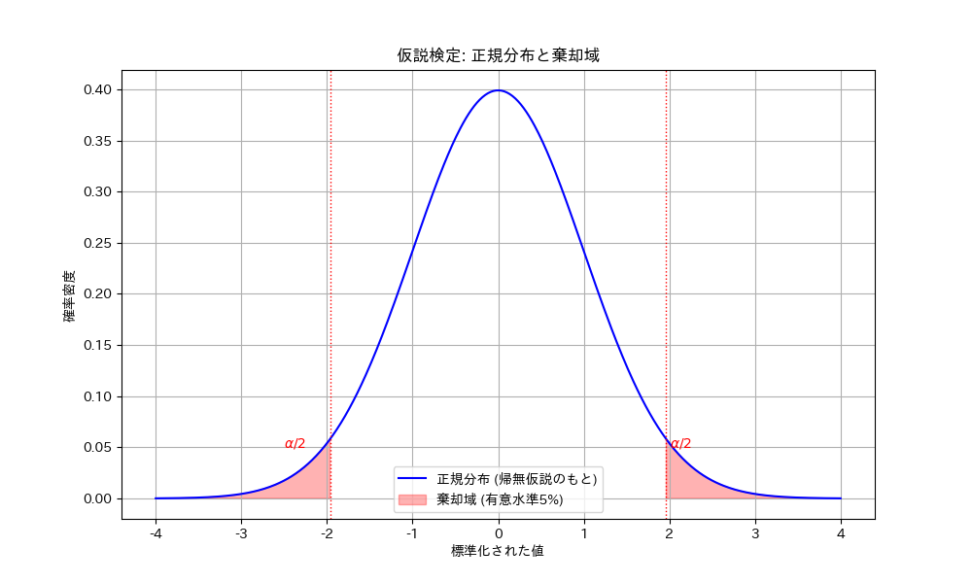
この「ほとんど起こりえない」という判断の基準となるのが「有意水準（Significance Level）」です。これは、帰無仮説が正しいにもかかわらず、誤って帰無仮説を棄却してしまう確率（第一種の過誤）を、あらかじめ設定しておくものです。

仮説検定と他の概念の繋がり：p値

仮説検定の根幹には確率論があります。

得られたデータが帰無仮説のもとでどれくらい起こりにくいかを評価する際に、${p}$値（ピーち）という確率を用います。${p}$値は、「帰無仮説が正しいと仮定したときに、観測されたデータ、あるいはそれよりも極端なデータが得られる確率」を示します。この${p}$値が有意水準よりも小さければ、帰無仮説を棄却します。

つまり、${p}$値は、データが帰無仮説とどれくらい矛盾しているかを示す指標なのです。

統計学を学ぶことの意義

ここまで、統計学の基本的な考え方や概念を解説してきました。統計学は、単に数字を計算する技術というよりは、不確実な世界を理解し、データに基づいてより良い意思決定を行うためのツールです。

どんな嬉しいことがある？：データに基づいた思考力と批判的思考力

統計学を学ぶことで、まず「データに基づいた思考力」を身につけることができます。巷にあふれる情報やニュース、ビジネスの報告書など、多くのものがデータや統計的な主張を含んでいます。

ある程度の知識があれば、それらの情報が本当に信頼できるものなのか、どのような前提に基づいているのかを批判的に評価できるようになります。例えば、

「この調査結果は、本当にその結論を支持しているのか？」

「サンプルサイズは十分か？」

「統計的に有意な差とはどういう意味か？」

といった問いを立て、データの全体像を推し量る力が養われると思います。

どんな嬉しいことがある？：問題解決と意思決定

上でもコメントしていますが、ビジネスの現場では、日々様々な意思決定が求められると思います。

「このバナー広告に変更して、流入は増えたんだっけ？」

「在庫を最小限にするために、店舗Aに卸す商品の量って、どうやって決めるべきだっけ？」

「どの顧客層にアプローチするのが、最もROIが良いのか」

といった問いに対し、統計学は客観的なデータに基づいた根拠を提供します。

勘や経験に頼るだけでなく、データという客観的な証拠に基づいて判断を下すことで、よりリスクを低減し、成功確率を高めることができます。

統計検定への道：知識を形にする

統計学の学習を進める中で、自身の知識を客観的に評価したいと考える方もいるでしょう。そのための有効な手段の一つが「統計検定」です。

統計検定は、統計に関する知識や活用力を評価する全国統一試験であり、ビジネスや学術の様々な分野でその価値が認められています。特に、統計検定2級は、大学基礎課程で学ぶ統計学の知識を問うもので、データサイエンスの基礎を固める上で役立ちます。

この解説記事で学んだ概念は、統計検定の学習においても基礎となります。

問題から解いてみたい方は、青の統計学Ds playgroundの問題演習に取り組んでみてください。