【計量経済学】IPW推定量をわかりやすく解説|因果推論
こんにちは、青の統計学です。
今回は、計量経済学の授業などで傾向スコアとともに出てくるIPW推定量について解説いたします。

めっちゃ簡単にいうと、傾向スコアは「処置を受ける確率」そのもので、IPW推定量は「その確率の逆数で重み付けして因果効果を測る手法」です。
IPW推定量とは何か?
IPW推定量は、その名の通り「逆確率重み付け(Inverse Probability Weighting)」という手法を用いて、因果効果を推定する統計量です。この手法の核心は、データに存在する偏りを、適切な重みを与えることで補正し、あたかもランダム化されたかのような状況を作り出す点にあります。

つまり、観測データがランダム化されていないために生じるバイアスを取り除き、公平な比較を可能にするための工夫の一つですね。現実では、RCTできない場合もザラにあるので、よく検討される手法かと思います
傾向スコアの直感的理解
IPWを理解する上で欠かせないのが「傾向スコア(Propensity Score)」という概念です。傾向スコアとは、簡単に言えば「ある個人が、その人が持っている様々な特徴(共変量)に基づいて、特定の処置(例えば、新しい学習方法を受ける、特定の薬を服用するなど)を受ける確率」のことです。
数式で表すと、ある個体$i$の共変量を$X_i$、処置を受けるかどうかを$T_i$($T_i=1$なら処置群、$T_i=0$なら対照群)としたとき、傾向スコア$e(X_i)$は次のように定義されます。
$${e(X_i) = P(T_i=1 | X_i)}$$
つまり、共変量$X_i$が与えられた下で、処置$T_i=1$となる条件付き確率ですね。
傾向スコアの嬉しさ
例えば、新しい学習方法の効果を評価したいとします。この学習方法を自ら選択した学生(処置群)と、選択しなかった学生(対照群)を比較すると、もともと学習意欲の高い学生が新しい学習方法を選択する傾向があるかもしれません。この場合、学習意欲という共変量が、学習方法の選択(処置)とテストの点数(結果)の両方に影響を与える「交絡因子」となります。単純に両グループのテストの点数を比較しても、学習方法の効果なのか、それとも学習意欲の高さによるものなのかが区別できません。
ここで傾向スコアを使います。
学習意欲が高い学生は、新しい学習方法を選択する確率(傾向スコア)が高いでしょう。逆に、学習意欲が低い学生は、選択する確率が低いかもしれません。
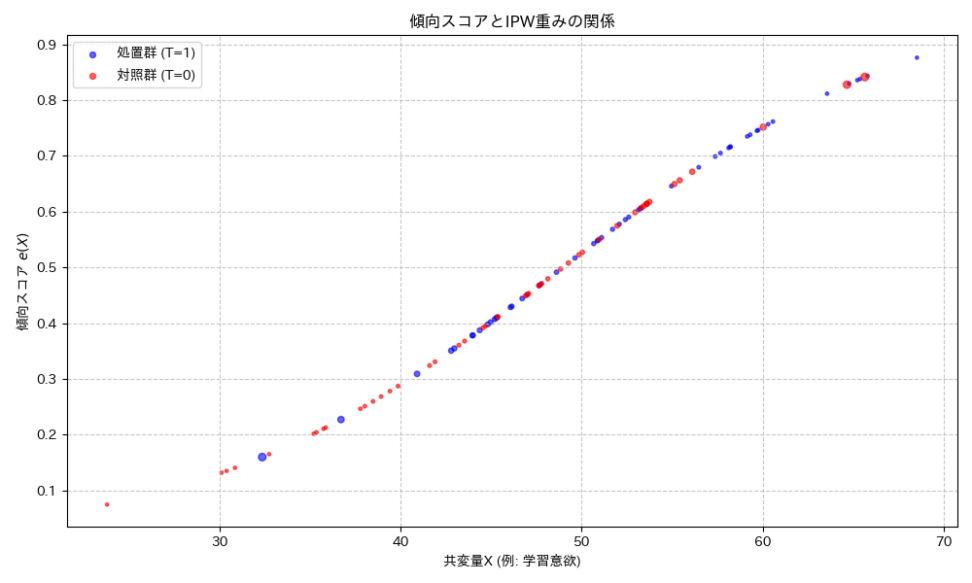
傾向スコアを用いることで、学習意欲などの共変量の影響を調整し、処置群と対照群を「公平に」比較できるような状況を作り出すことができます。つまり、傾向スコアが同じであれば、学習方法を選択したかどうかがランダムに決まったとみなせる、というわけです。
おまけ|交絡因子について
データ分析において、避けるべき問題の一つが「交絡(Confounding)」です。交絡とは、処置(原因)と結果の両方に影響を与える第三の要因(交絡因子)が存在することで、見かけ上の相関が因果関係ではないのに、あたかも因果関係があるかのように見えてしまう現象です。例えば、喫煙と肺がんの関係を調べるとき、年齢や性別、職業などが交絡因子となる可能性があります。これらの因子は喫煙行動にも肺がんの発症にも影響を与えるため、単純に喫煙者と非喫煙者の肺がん発症率を比較しても、喫煙の純粋な因果効果を推定することはできませんよね。
IPW推定量は、この交絡によるバイアスを軽減するために開発されました。傾向スコアを用いて各個体に適切な重みを与えることで、処置群と対照群の共変量の分布をバランスさせ、交絡因子の影響を統計的に除去します。これにより、観察研究においても、あたかもランダム化比較試験(RCT)のような、交絡が調整された比較が可能になります。つまり、IPWは、データ分析における公平な比較に近づくための手段というわけです。
逆確率重み付けのメカニズム
傾向スコアの理解が深まったところで、いよいよ「逆確率重み付け」のメカニズムを見ていきましょう。IPWの基本的なアイデアは、観測されたデータに「重み」を付けることで、データの偏りを補正し、あたかもランダム化比較試験のような理想的な状況を再現することです。
具体的には、各個体のデータに、その個体が観測された確率の「逆数」を重みとして与えます。
というか、なぜ逆数なのでしょうか?
例えば、ある特定の共変量を持つ学生グループを考えます。このグループの中で、新しい学習方法を選択する学生はごく少数だったとします。つまり、このグループの学生が新しい学習方法を選択する傾向スコアは非常に低い(例えば0.1)ということです。しかし、もしこの「ごく少数」の学生が新しい学習方法を選択したとします。この学生は、本来なら新しい学習方法を選択する確率が低いにもかかわらず、たまたま選択した「珍しい」学生と考えることができます。
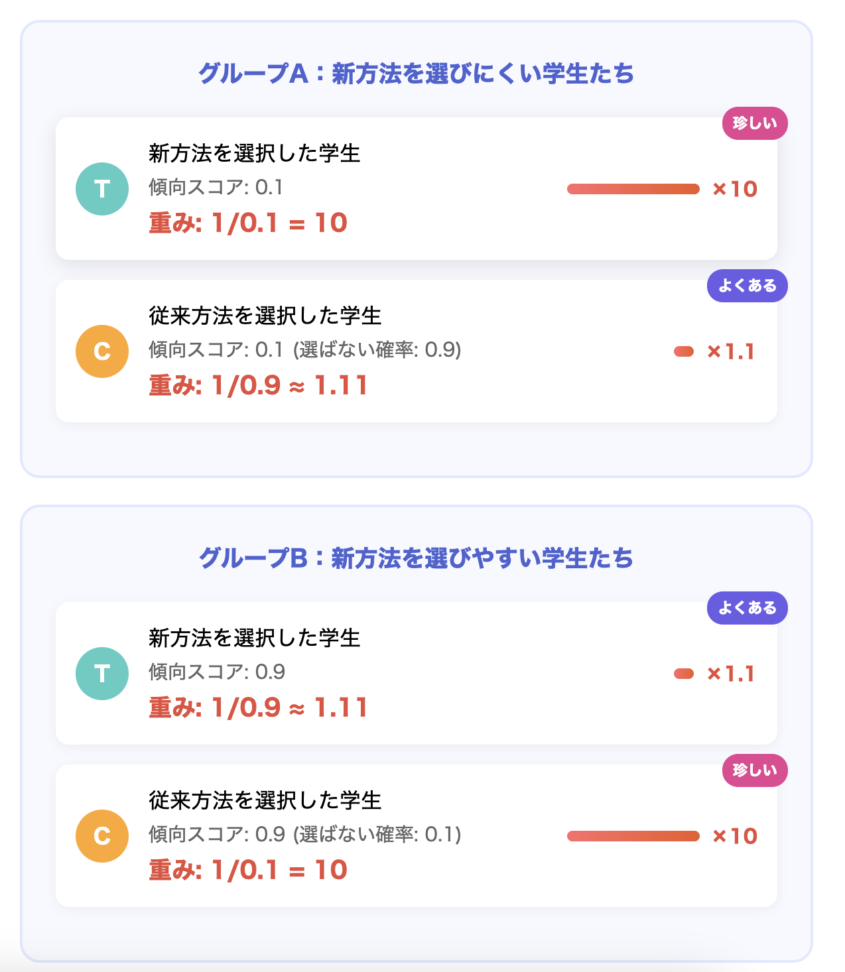
このような「珍しい」学生のデータは、そのグループ全体における新しい学習方法の効果を代表する上で、より大きな意味を持つべきだと考えられます。そこで、傾向スコアの逆数(1/0.1 = 10)を重みとして与えることで、要はこの珍しい学生のデータを増幅させ、そのグループ全体における代表性を高めるのです。
逆に、新しい学習方法を選択する確率が高い(例えば0.9)学生が、実際に新しい学習方法を選択したとします。この学生は「よくある」ケースなので、重みは傾向スコアの逆数(1/0.9 ≈ 1.11)となり、あまり増幅されません。
処置を受けなかった学生についても同様です。処置を受けない確率($1 – e(X_i)$)の逆数を重みとして与えます。つまり、処置群の個体には$1/e(X_i)$、対照群の個体には$1/(1-e(X_i))$という重みを与えることで、データの偏りを補正し、処置群と対照群の共変量の分布をバランスさせることができるのです。
これにより、交絡の影響を取り除き、処置の純粋な効果を推定することが可能になります。

この重み付けによって、私たちは「もし全員が処置を受けたらどうなるか」「もし全員が処置を受けなかったらどうなるか」という、現実には観測できない「潜在的アウトカム」を、観測データから推定できるようになるのです。
数学的背景:IPW推定量の定式化
IPW推定量の背後には、因果推論の厳密な枠組みと、確率論に基づいた数学的な定式化があります。
潜在的アウトカムと因果効果
因果推論の議論は、「潜在的アウトカム(Potential Outcomes)」という概念から始まります。これは、もしある個体が特定の処置を受けた場合にどうなるか、あるいは受けなかった場合にどうなるか、という反実仮想の世界の結果を考えるものです。
個体$i$について、
- 処置を受けた場合の潜在的アウトカムを$Y_i(1)$
- 処置を受けなかった場合の潜在的アウトカムを$Y_i(0)$
と表します。
しかし、現実には、個体$i$は処置を受けるか受けないかのどちらか一方しか経験できません。つまり、$Y_i(1)$と$Y_i(0)$の両方を同時に観測することは不可能です。観測されるアウトカム$Y_i$は、個体$i$が実際に受けた処置$T_i$($T_i=1$なら処置、$T_i=0$なら非処置)に応じて、
$$Y_i = T_i Y_i(1) + (1-T_i) Y_i(0)$$
となります。
私たちが一貫して知りたいのは、処置がアウトカムに与える「因果効果」です。
最も一般的な因果効果の指標は、「平均処置効果(Average Treatment Effect, ATE)」です。これは、集団全体における処置の平均的な効果を指し、次のように定義されます。
$${ATE = E[Y(1) – Y(0)] = E[Y(1)] – E[Y(0)]}$$
${E}$は期待値を表します。つまり、もし全員が処置を受けたら得られる平均的なアウトカム$E[Y(1)]$と、もし全員が処置を受けなかったら得られる平均的なアウトカム$E[Y(0)]$の差がATEです。
傾向スコアの定義
先ほども触れましたが、傾向スコア$e(X)$は、共変量$X$が与えられた下で、処置を受ける確率として定義されます。
$${e(X) = P(T=1 | X)}$$
この傾向スコアは、通常、ロジスティック回帰モデルなどを用いて推定されます。例えば、共変量$X$を用いて処置$T$を予測するモデルを構築し、その予測確率を傾向スコアとするわけです。
傾向スコアが正しく推定されていれば、傾向スコアが同じ個体間では、処置の割り当てがランダムであるとみなすことができます。これを「条件付き交換可能性(Conditional Exchangeability)」と呼びます。
つまり、
$$(Y(1), Y(0)) \perp T | X$$
が成り立つということです。
Horvitz-Thompson推定量
IPW推定量の最も基本的な形は、Horvitz-Thompson推定量に由来します。これは、標本抽出の確率が不均一な場合に、その確率の逆数で重み付けを行うことで、母集団の特性を不偏に推定するという考え方です。因果推論の文脈では、処置を受ける確率(傾向スコア)が標本抽出の確率に相当します。
$E[Y(1)]$のIPW推定量は、処置群の観測データ$Y_i$を、その個体が処置を受けた確率$e(X_i)$の逆数で重み付けして平均することで得られます。同様に、$E[Y(0)]$のIPW推定量は、対照群の観測データ$Y_i$を、その個体が処置を受けなかった確率$1-e(X_i)$の逆数で重み付けして平均することで得られます。
具体的には、ATEのIPW推定量は次のように表されます。
$${ \text{ATE}_{ \text{IPW}} = \frac{1}{N} \frac{T_i Y_i}{e(X_i)} – \frac{1}{N} \frac{(1-T_i) Y_i}{1-e(X_i)} }$$
$N$は全サンプルサイズですね。
この式は、処置群のデータは${\frac{1}{e(X_i)}}$で、対照群のデータは$\frac{1}{(1-e(X_i)}$で重み付けされていることを示しています。この重み付けにより、処置群と対照群の共変量の分布がバランスされ、交絡の影響が除去されることで、ATEの不偏推定が可能になります。
おまけ|大数の法則とIPW推定量
IPW推定量がなぜ信頼できる推定値を与えるのか、その理論的な裏付けの一つが「大数の法則(Law of Large Numbers)」です。大数の法則とは、独立同分布に従う確率変数の標本平均は、サンプルサイズが大きくなるにつれて、その確率変数の期待値(母平均)に収束するという統計学の基本的な定理です。
IPW推定量は、重み付けされた標本平均の形をしています。傾向スコアの逆数で重み付けされた各個体のアウトカムは、ある意味で「仮想的な母集団」からの標本と見なすことができます。サンプルサイズが十分に大きくなれば、この重み付けされた標本平均は、真の平均処置効果(ATE)に収束することが理論的に示されています。この性質を「一致性(Consistency)」と呼びます。つまり、データが多ければ多いほど、IPW推定量は真の因果効果に近づいていく、というわけです。これは、IPW推定量の信頼性を保証する漸近的性質です。
Hajek推定量:安定性の追求
もう一つ紹介しておきましょう。
Horvitz-Thompson推定量は不偏性を持つ一方で、傾向スコアが0に近い、または1に近い個体が存在する場合、重みが非常に大きくなり、推定量の分散が大きくなるという指摘があります。これは、極端な重みを持つ少数のデータ点が、推定結果に過度に影響を与えてしまうためです。
この問題を緩和するために提案されたのが、「Hajek推定量」です。
Hajek推定量は、重みの合計を1に正規化することで、推定量の安定性を高めます。具体的には、各グループ(処置群と対照群)内で重みを正規化します。
処置群における$E[Y(1)]$のHajek推定量は:
$${ \frac{ \frac{1}{N} \frac{T_i Y_i}{e(X_i)}}{ \frac{1}{N} \frac{T_i}{e(X_i)}} }$$
対照群における$E[Y(0)]$のHajek推定量は:
$${ \frac{ \frac{1}{N} \frac{(1-T_i) Y_i}{1-e(X_i)}}{ \frac{1}{N} \frac{(1-T_i)}{1-e(X_i)}} }$$
となります。
つまり、分子はHorvitz-Thompson推定量と同じですが、分母で重みの合計で割ることで正規化しています。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!






