【完全ガイド】k-means法とは？周辺のクラスタリング手法と比較

クラスタリングのモチベーション

クラスタリングは、似た特徴を持つデータをグループ分けすることで、顧客セグメンテーション、マーケティング戦略、異常検知などの幅広いビジネス課題に対応するための手法です。

データの集合をグループ化するタスクのことをクラスタリングといい、各グループはクラスターと呼ばれます。同じクラスター内のデータは、他のクラスター内のデータよりも類似性が高くなります。

中でもK-meansは、そのシンプルさと高速な計算能力により、初期分析から実運用まで広く利用されています。

この記事では、K-meansおよびその拡張手法（K-means++、X-means、ソフトK-means、ファジィC-means）について、数学的背景や実装例を通して深堀りしていきます。

シミュレーションしながらだと学習効率がぐっと上がるので、以下のツールを見ながらの学習をお勧めします！

クラスタリング可視化ツール

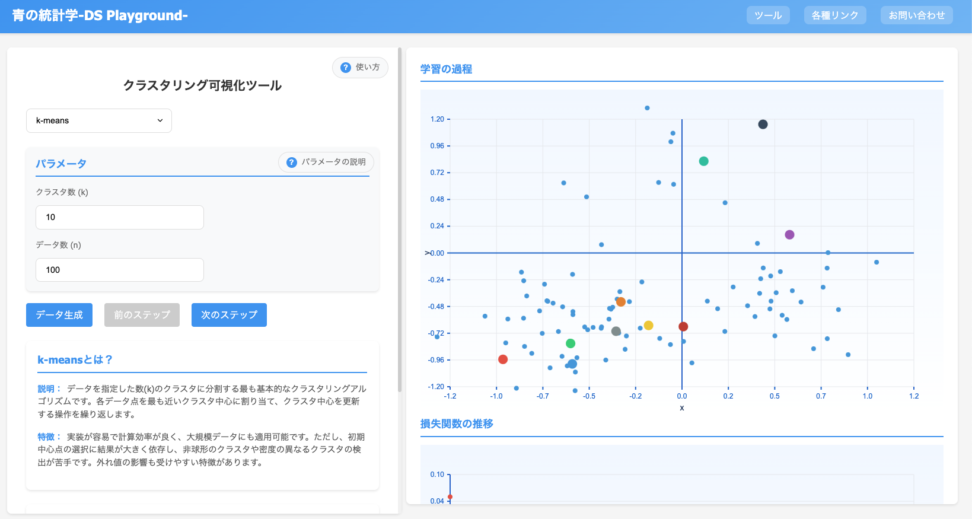
K-meansとは？

K-meansは、各クラスタ内のデータのばらつきを最小化することを目的としたアルゴリズムです。
その目的関数は、各クラスタ$S_i$のセントロイド$\mu_i$とデータ点$x$との二乗ユークリッド距離の総和を最小化するもので、数学的には次のように表されます。

$${\underset{S}{\operatorname{arg\,min}} \sum_{i=1}^{k} \sum_{x \in S_i} \| x – \mu_i \|^2S}$$

$\mu_i$はクラスタ$S_i$の平均として、

$${\mu_i = \frac{1}{|S_i|} \sum_{x \in S_i} x}$$

と定義されます。

具体的には、以下のステップを反復的に実行します。

• 割り当てステップ
  • 各データ点$x_i$に対して、最も近いセントロイド$\mu_k$を見つけ、 ${c_i = \underset{k}{\operatorname{arg\,min}} \| x_i – \mu_k \|^2}$として割り当てます。
• 更新ステップ
  • 各クラスタにおける新たなセントロイドを、割り当てられたデータ点の平均として再計算します。

このシンプルな反復プロセスが、クラスタ内の分散を着実に低減させ、局所最適解に収束するという仕組みです。

k-meansの直感的理解

１：分けたいクラスターの数だけ、とりあえず点を置きます。

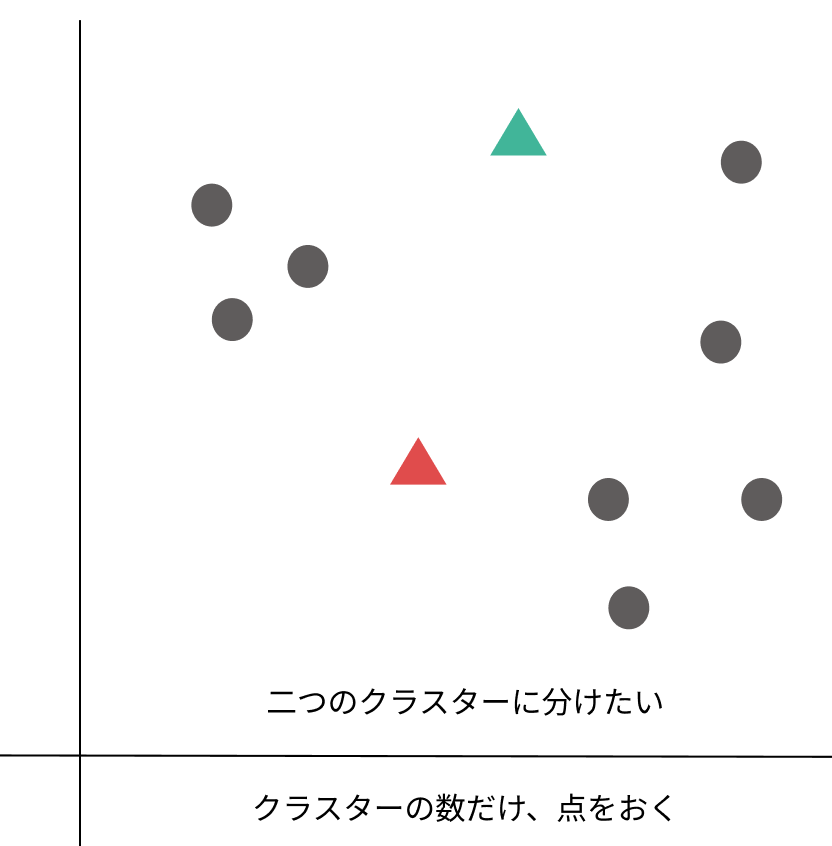
＊点（セントロイド）を置く位置で最終的に作られるクラスターが変わる場合もあります。

2：点と各データの距離を測り、近い方のクラスターに分ける。

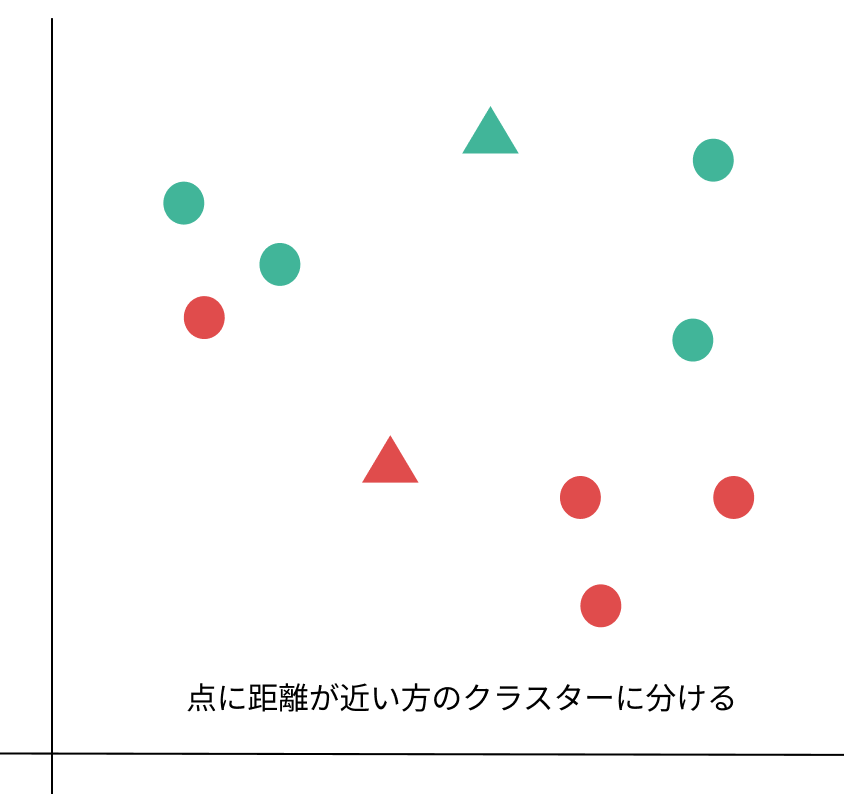
3：分けたクラスター内で平均をとり、新しい基準点に変える。

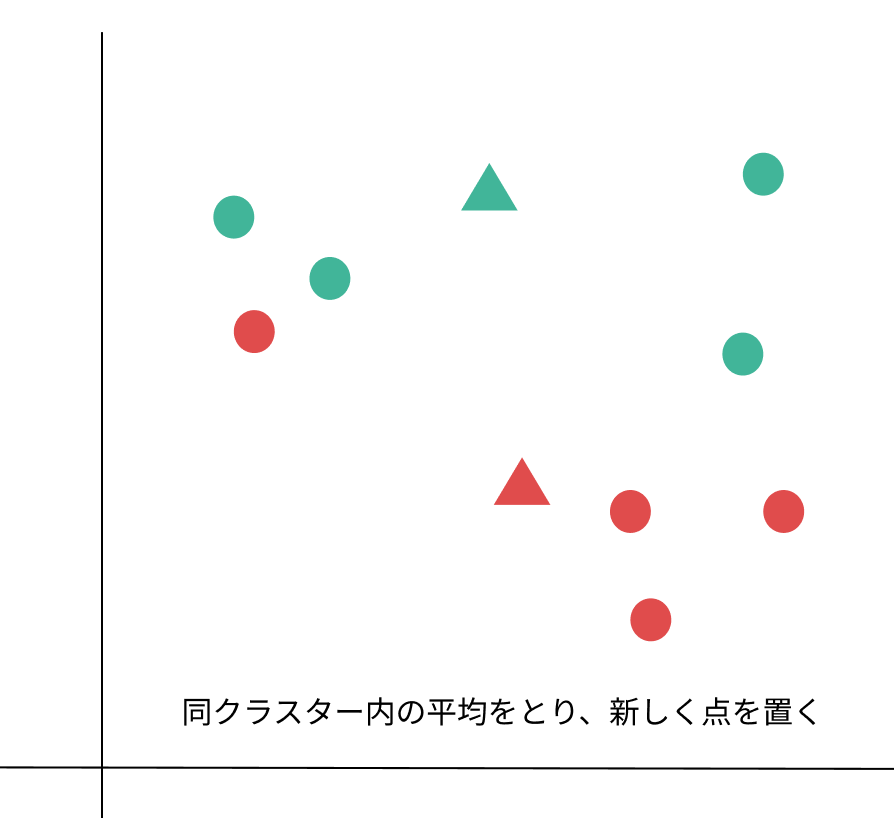
4：同じように新しい基準点と各データの距離を測り、近い方のクラスターに分ける

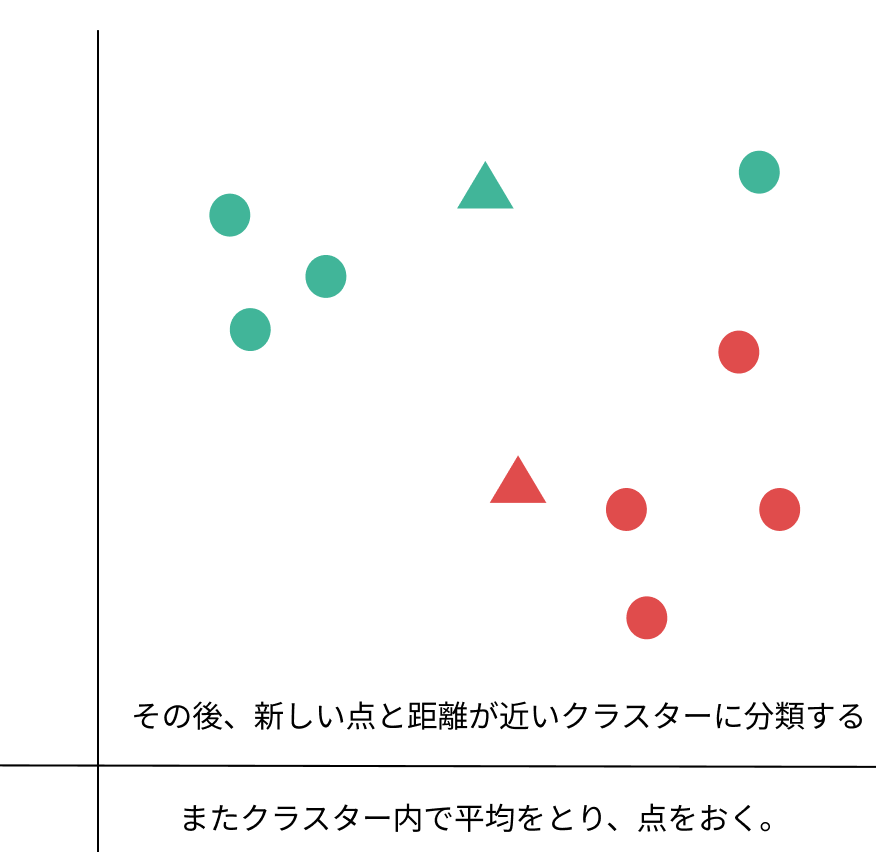
裏側では、各データとそれが割り当てられるクラスタ中心の平方ユークリッド距離が最小化する最適化問題を解いている、というわけです。

k-means法は、教師なし学習のクラスタリングの中でも「非階層型」と呼ばれる型に分類されます。非階層型の短所として、事前にクラスターを何個作るかを指定してあげることが必要になります。

その代わり、次元数が多くても対応可能という長所はあります。

	メリット	デメリット
非階層	次元が多い場合にも対応する	事前にクラスター個数を指定する
階層	分類過程を視覚的に見れる	計算量が多い

事前にクラスターの数を指定しない階層型ですが、正解データがなく解釈や評価が難しい教師なし学習では大きな問題点と思われるかもしれませんね。

局所解と大域解

実際に、k-means法によって得られるクラスタリング結果はクラスタリングの初期状態に大きく依存する局所最適解です。

大域的な最適解を求めるには、複数の初期状態でクラスタリングを行い、その中から最も良い結果を選ぶことが大切であり、その良し悪しは先ほどのコスト関数（損失関数）が小さいものを選べば良い、ということになります。

$${f(x)=argmin||x_{n}-μ_{k}||^2}$$

K-means++とは？

K-meansの初期化問題

K-meansアルゴリズムの大きな課題の一つは、初期セントロイドの選択に対する感度です。K-meansはランダムにセントロイドを選択するため、次のような問題が発生することがあります。

1. 局所最適解に陥る
   • クラスタの分布によっては、適切でない初期セントロイドが選ばれ、最適なクラスタリングが得られない。
2. 収束が遅くなる
   • 初期のセントロイドが適切でない場合、収束までの反復回数が増加する。
3. クラスタのバランスが悪くなる
   • セントロイドが偏った位置に配置されると、一部のクラスタが大きくなりすぎたり、逆に小さくなりすぎたりする。

この問題を解決するために登場したのが K-means++ です。

K-means++の仕組み

K-means++は、初期セントロイドの選択をより賢く行うことで、K-meansの収束速度とクラスタリング精度を向上させる手法です。

具体的には、次の手順で初期セントロイドを決定します。

1. 最初のセントロイドをランダムに1つ選択
   • データセット$X$の中から1つのデータ点をランダムに選ぶ。
2. 各データ点と既存のセントロイドの最短距離を計算
   • 残りのデータ点$x$に対して、既に選ばれたセントロイドの中で最も近いものとの二乗ユークリッド距離を計算する。
   • 距離を$D(x)$とする。
3. 確率的に新しいセントロイドを選択
   • 各データ点$x$が次のセントロイドに選ばれる確率を、$D(x)^2$に比例させる。
   • つまり、遠く離れたデータ点ほど選ばれやすくなる。
4. 必要な数のセントロイドを選択するまで2〜3を繰り返す

このプロセスのポイントは、すでに選ばれたセントロイドから遠くにある点を優先的に選ぶことです。

数学的な考察

K-means++の初期化手法は、理論的にK-meansの最適解の$O(\log k)$倍以内の良い解を保証する近似アルゴリズムです。

確率分布として、次のように新しいセントロイド$x_i$を選択します。

$${P(x) = \frac{D(x)^2}{\sum_{x’ \in X} D(x’)^2}}$$

$D(x)$：$x$と最も近い既存のセントロイドとの距離

この確率分布によって、

• すでにカバーされた領域から新たなセントロイドが選ばれるのを防ぐ
• クラスタが自然な広がりを持つようにする

という効果が得られます。

X-meansとは？

K-meansの課題: クラスタ数$k$の決定

そもそも、K-meansの大きな欠点の一つは、クラスタ数$k$を事前に決めなければならないことです。
適切な$k$を見つけるためには、エルボー法やシルエットスコアといった手法を使って試行錯誤する必要がありますが、これは手間がかかり、データに対する明確な知識がない場合には適切な$k$を選ぶのが意外と難しくなります。

この問題を解決するために考案されたのが X-means です。

X-meansの仕組み

X-meansは、以下の手順でクラスタ数$k$を最適化します。

1. 小さな$k$（例えば$k_{\min} = 2$）でK-meansを実行する
   • 通常は最小クラスタ数（例えば2）から開始し、データ全体を少数のクラスタに分割。
2. 各クラスタを2つに分割し、ローカルなK-meansを実行する
   • クラスタ内のデータをさらに分割できるかどうかを確認。
   • もし分割できるなら、新たなクラスタとして扱う。
3. ベイズ情報量基準（BIC）または赤池情報量基準（AIC）を用いて、分割の妥当性を評価
   • クラスタ数が増えると柔軟な分類が可能になるが、過学習のリスクもある。
   • BIC/AICは、モデルの複雑さと適合度のバランスを取るために使われる。
   • クラスタ分割後のスコアが向上するなら、新たなクラスタを採用し、そうでなければ分割をキャンセル。
4. 上記の手順を、クラスタが分割されなくなるまで繰り返す

数学的な考察: BICによる評価

クラスタ数$k$が適切かどうかを判断するために、X-meansは ベイズ情報量基準（BIC） を用います。BICは、統計モデルの適合度とモデルの複雑さを天秤にかけ、より適切な$k$を選ぶ基準です。

BICの数式は次のように表されます。

$${BIC = L – \frac{p}{2} \log N}$$

• $L$: クラスタリング後の対数尤度
• $p$: 推定されたパラメータの数（クラスタ数$k$に依存）
• $N$: データ点数

BICが最大となる$k$を採用することで、適切なクラスタ数を決定できます。

さて、X-meansは、あらかじめクラスタ数$k$を指定する必要があるK-meansの問題点を解消すべく、初期クラスタ数（通常は最小値$k_{\min}$）から開始し、各クラスタの分割可能性を統計的基準に基づいて評価する、という手法だとわかりました。

分割が適切と判断されると、クラスタは二分割され、最適なクラスタ数に近づけていきます。

ソフトK-meansとは？

K-meansの限界：ハードなクラスタ割り当て

K-meansでは、各データ点は必ず1つのクラスタに割り当てられるという前提があります。これは「ハードクラスタリング」と呼ばれ、データ点が明確に分かれる場合には適しています。

しかし、次のようなケースでは問題が生じます。

1. クラスタの境界が曖昧な場合
   • 例：顧客セグメンテーションで、ある顧客が2つの異なるグループの特徴を持つ場合。
2. データが連続的に分布している場合
   • 例：異なる色のグラデーション画像をクラスタリングする場合。
3. 異常検知など、不確実性が重要な場合
   • 例：金融データの異常値検出では「正常」と「異常」の間にグレーゾーンが存在する。

このような状況に対応するためには、 ソフトK-means（確率的K-means） が使えます。

ソフトK-meansの仕組み

ソフトK-meansでは、各データ点が複数のクラスタに対して「確率的な所属度」を持ちます。
具体的には、データ点$y_n$がクラスタ$k$に属する確率 $z_{nk}$ を計算し、それをクラスタ割り当ての基準とします。

この確率 $z_{nk}$ は、以下のソフトマックス関数を用いて計算されます。

$${z_{nk} = \frac{\exp\left(-\frac{\|y_n – \mu_k\|^2}{\beta}\right)}{\sum_{j=1}^{K}\exp\left(-\frac{\|y_n – \mu_j\|^2}{\beta}\right)}}$$

• $\mu_k$ ：クラスタ$k$のセントロイド（中心）
• $\beta$ ：「温度パラメータ」で、確率の鋭さを調整する役割を持つ

この式により、各データ点が異なるクラスタに対してどの程度属するかを確率的に表現できます。

手法	クラスタ割り当て	計算コスト	適用範囲
K-means	ハード（1クラスタのみ）	低い	明確なクラスタ
ソフトK-means	確率的	やや高い	不確実性があるデータ

ファジィC-meansとは？

K-meansとソフトK-meansの限界

これまで見てきたK-meansやソフトK-meansは、それぞれ以下のような課題を抱えています。

1. K-means
   • データ点は 厳密に1つのクラスタ に所属する（ハードクラスタリング）。
   • クラスタの境界が曖昧な場合に適用が難しい。
2. ソフトK-means
   • データ点のクラスタ所属度を確率として表現するが、確率の合計が1になるため、
     データ点が複数のクラスタに同時に強く属することはできない。

そこで、ファジィC-means（Fuzzy C-means, FCM） です。
FCMでは、データ点が すべてのクラスタに対して異なる程度のメンバシップ（所属度）を持つ という考え方を採用します。

ファジィC-meansの仕組み

FCMでは、各データ点$x_i$が各クラスタ$j$に対して メンバシップ値 $u_{ij}$（0から1の間）を持ちます。
つまり、1つのデータ点が複数のクラスタにまたがって所属することが可能です。

このメンバシップ値を用いて、以下の目的関数を最小化することでクラスタリングを行います。

$${J_m = \sum_{i=1}^{N} \sum_{j=1}^{C} (u_{ij})^m ||x_i – c_j||^2}$$

• $N$：データ点の総数
• $C$：クラスタ数
• $u_{ij}$：データ点$x_i$のクラスタ$j$へのメンバシップ（0 ≤ $u_{ij}$ ≤ 1）
• $c_j$：クラスタ$j$のセントロイド（重心）
• $m$：ファジィネスパラメータ（$m > 1$）
  • $m$が大きいほどクラスタの境界が曖昧になり、小さいほどK-meansに近づく。

この目的関数は、各データ点のクラスタ中心への距離の加重平均 を最小化するように働きます。

クラスタ中心とメンバシップ値の更新

FCMでは、次の2つの式を用いて メンバシップ行列 と クラスタ中心 を更新しながら収束させます。

1. クラスタ中心の更新

$${c_j = \frac{\sum_{i=1}^{N} (u_{ij})^m x_i}{\sum_{i=1}^{N} (u_{ij})^m}}$$

2. メンバシップ値の更新

$${u_{ij} = \frac{1}{\sum_{k=1}^{C} \left(\frac{||x_i – c_j||}{||x_i – c_k||}\right)^{\frac{2}{m-1}}}}$$

この繰り返し計算により、

• クラスタ中心がデータの分布に基づいて移動 し、
• メンバシップ値が各データ点に対して更新される
  というプロセスを経て収束します。

ファジィネスパラメータ$m$の影響

ファジィC-meansの大きな特徴は、ファジィネスパラメータ$m$ によってクラスタの境界の曖昧さを調整できることです。

この辺は、実際にシミュレーションをしないと訳がわからないと思うので、以下ツールで学んでいただくのが良いかと思います。

クラスタリング可視化ツール

• $m$ が 1 に近づくと → FCMはK-meansに近づき、データ点は1つのクラスタにほぼ完全に属する。
• $m$ が大きくなると → クラスタの境界がぼやけ、すべてのデータ点が複数のクラスタにまたがるようになる。

まとめ

5つのクラスタリング手法の主な違いをまとめてみます。

特徴	K-means	K-means++	X-means	ソフトK-means（確率的K-means）	ファジィC-means
目的	WCSSの最小化	WCSSの最小化	WCSSの最小化（分割にBIC/AICを使用）	距離に基づく確率的割り当て	ファジィメンバシップによる加重WCSSの最小化
初期化	k個のセントロイドをランダムに選択	セントロイドを分散させるスマートな初期化	通常、小さなkでK-meansを実行することから開始	k個のセントロイドをランダムに選択	メンバシップ行列をランダムに初期化
割り当て	最も近いセントロイドへのハード割り当て	最も近いセントロイドへのハード割り当て	最も近いセントロイドへのハード割り当て	すべてのクラスタへの確率的割り当て	すべてのクラスタへのファジィ割り当て（メンバシップの程度）
クラスタ数	固定されたk（ユーザーが事前に定義）	固定されたk（ユーザーが事前に定義）	自動的に決定	固定されたk（ユーザーが事前に定義）	固定されたk（ユーザーが事前に定義）
クラスタ形状	球形、ほぼ同じサイズを想定	球形、ほぼ同じサイズを想定	凸形状になりやすい	さまざまな形状を処理可能（GMMに関連）	さまざまな形状を処理可能
オーバーラップ処理	なし	なし	明示的なオーバーラップ処理なし	確率的なオーバーラップを許容	ファジィオーバーラップを許容（メンバシップの程度）
数学的基礎	分散の最小化、ベクトル量子化	K-meansの初期化を改善	モデル選択のための統計的基準	ガウス混合モデルとの関連	ファジィ集合論、反復最適化

結局どう使い分ける？

各クラスタリングアルゴリズムの典型的なアプリケーションについて簡単に説明します。

• K-means
  • 顧客セグメンテーション、画像圧縮、文書クラスタリング、異常検出、配送ルート最適化、不正検出、アカウント解約の予測、顧客インセンティブのターゲティング、サイバー犯罪の特定 ¹。
• K-means++
  • K-meansと同様のアプリケーションで、より良い初期化により信頼性と速度が向上。画像セグメンテーション、顧客セグメンテーション、レコメンデーションシステムで使用 ¹。
• X-means
  • クラスタ数が不明なアプリケーション（生物学的データ分析、画像分析、ワイヤレスセンサーネットワーク、幼児期疾患のグループ化など） ¹⁶。
• ソフトK-means
  • 確率的なクラスタ割り当てが有益なシナリオ（画像セグメンテーション、顧客セグメンテーション、異常検出、より複雑な確率モデルへのステップなど） ¹⁷。
• ファジィC-means
  • 画像セグメンテーション（特に医用画像処理）、パターン認識、バイオインフォマティクス（遺伝子発現解析）、マーケティング（重複する嗜好に基づく顧客セグメンテーション）、化学イオン化質量分析の解析 ¹⁹。

メリデメ整理

各アルゴリズムの主な利点と欠点をまとめます。

• K-means
  • 利点: 理解と実装が容易、計算効率が高い、大規模データセットにスケーラブル、容易に適応可能 。
  • 欠点: 初期セントロイドの選択に敏感、kの事前指定が必要、外れ値に敏感、ほぼ同じサイズの球形クラスタを想定、局所最適解に陥る可能性あり
• K-means++
  • 利点: 標準的なK-meansと比較して初期セントロイドの選択に対する感受性が低い、収束が速く、クラスタリング品質が向上することが多い
  • 欠点: kの事前指定が必要、他のK-meansの制限（外れ値への感受性、球形クラスタの仮定）を共有、非常に大きなデータセットの場合、初期化の計算コストが高くなる可能性がある 。
• X-means
  • 利点: クラスタ数を自動的に決定、推測されたkを持つK-meansよりも優れたクラスタリングを生成することが多い
  • 欠点: K-meansよりも計算コストが高くなる可能性があり（反復的な分割と評価を伴うため）、結果はkの初期範囲に依存する可能性があり、依然として準最適な解に収束する可能性がある
• ソフトK-means
  • 利点: 確率的なクラスタ割り当てを提供、オーバーラップするクラスタを処理可能、ハードクラスタリングよりも柔軟性がある
  • 欠点: 一般的にハードK-meansよりも計算コストが高い、パフォーマンスはスティフネスパラメータとクラスタ数の選択に敏感になる可能性がある ¹⁹。
• ファジィC-means
  • 利点: オーバーラップするクラスタを効果的に処理、各データ点の各クラスタへのメンバシップ度を提供、ハードクラスタリングと比較してノイズと外れ値に対してよりロバスト 。
  • 欠点: kとファジィネスパラメータmの事前指定が必要、K-meansよりも計算コストが高い、結果はmの選択に敏感になる可能性あり、局所最適解に収束する可能性もある 。