【多変量解析】ROC曲線とAUCによる判別分析|python
機械学習の問題は回帰問題と分類問題に大別されます。
そして、分類問題の指標でよく扱われるかつ、不均衡問題で威力を発揮する「ROC曲線」と「AUC」について今回は解説していきます。
統計検定準一級の範囲にもしっかり入っておりますので、受ける方はぜひご覧ください。
回帰問題についての評価指標については以下をご覧ください。
【MSEを最小化】ガウス・マルコフの定理と最良線形不偏推定量について
ROC曲線(receiver operating characteristic curve)とAUC(area under the ROC curve)
分類問題の指標を考える上で、一般的にはクラスラベルごとに分類を誤った際に被る損失を考慮します。
腫瘍が良性かどうかを腫瘍の画像から判別する問題を考えたとき、事態のマズさとしては、 「腫瘍が良性である人を、誤って悪性だと判別してしまうこと」 よりも 「腫瘍が悪性である人を、誤って良性だと判別してしまうこと」 の方が、後々大変になることは誰にでも想像のつくことです。
| 悪性と診断 | 良性と診断 | |
| 悪性 | TP | FN |
| 良性 | FP | TN |
例に挙げた内容の診断結果を事象として4つに分けることができると思います。
この行列を混同行列(confusion matrix)と呼びます。
TP(true positive):悪性を正しく診断できているケース。
FN(false negative):悪性を誤って良性と診断したケース。
FP(false negative):良性を誤って悪性と診断したケース。
TN(true negative):良性を正しく良性と診断したケース。
この概念は、第一種の過誤と第二種の過誤でも使われています。
詳しくは、【統計検定2級】第一種の過誤と第二種の過誤についてをご覧ください。
さて、4つのケースを使って以下のような分類手法が作れます。
①accuracy(正解率)
$$ACC(accuracy)=(\frac{TP+TN}{TP+TN+FP+FN})$$
これは一番分かりやすいと思います。例に準じると、「診断が当たっていたものの割合」となります。
全体として、どれだけ1と0を正確に予測できているかを見る指標が正解率ということですね。
ただし、正例と負例の分布が大きく偏っている場合には有効な指標であるとはいえません。
例えば、良性(負例)である確率が非常に高い場合、とりあえず良性だと診断しておけばaccracy自体は高くなってしまうからです。
②precision(適合率)
$$PRE(precision) = (\frac{TP}{T+FP})$$
適合率は、悪性と判断してしまったもののうち正しく分類できていたものの割合です。
1と予測した中で実際にどれだけ1であったかの割合です。異常検知システムがアラートを出した回数のうち、実際に異常であった割合などを想像してください。
③recall(再現率)
$$REC(recall)=(\frac{TP}{TP+FN})$$
再現率、真陽性率、感度などと呼ばれています。
こちらは悪性(正例)と判断すべきものの中で、正しく悪性と判断できていたものの割合です。
④specificity(特異度/真陰性率)
$$SPEC(specificity) = (\frac{TN}{TN+FP})$$
特異度、真陰性率と呼ばれます。
こちらは、良性(負例)だと分類すべきものの中で正しく良性だと判断できたものの割合です。
recallの逆ですね。
recallと1-specificity(偽陽性率)はトレードオフの関係にあります。
⑤F-1score
$$F1value = (\frac{2×recall×precision}{recall+precision})$$
F-1スコアは適合率(recall)と再現率(precision)の調和平均です。
適合率を優先すべきか、再現率を優先すべきかが決まっていない時点で、モデルを総合的に評価する場合などに使われます。
ROC(receiver operating characteristic curve)
以上のような指標に対して、ROCは「閾値の決め方によらない全体的な判別器の性能」を評価する方法として挙げられます。
先ほど挙げたrecallとトレードオフの関係にある1-specificityですが、これは偽陽性率と呼ばれるものであり
「負例なのに誤ってノイズを正例だと分類器が分類してしまう確率」です。
この偽陽性率を横軸にとり、真陽性率(recall)を縦軸に取った時にかける曲線をROC曲線と呼びます。
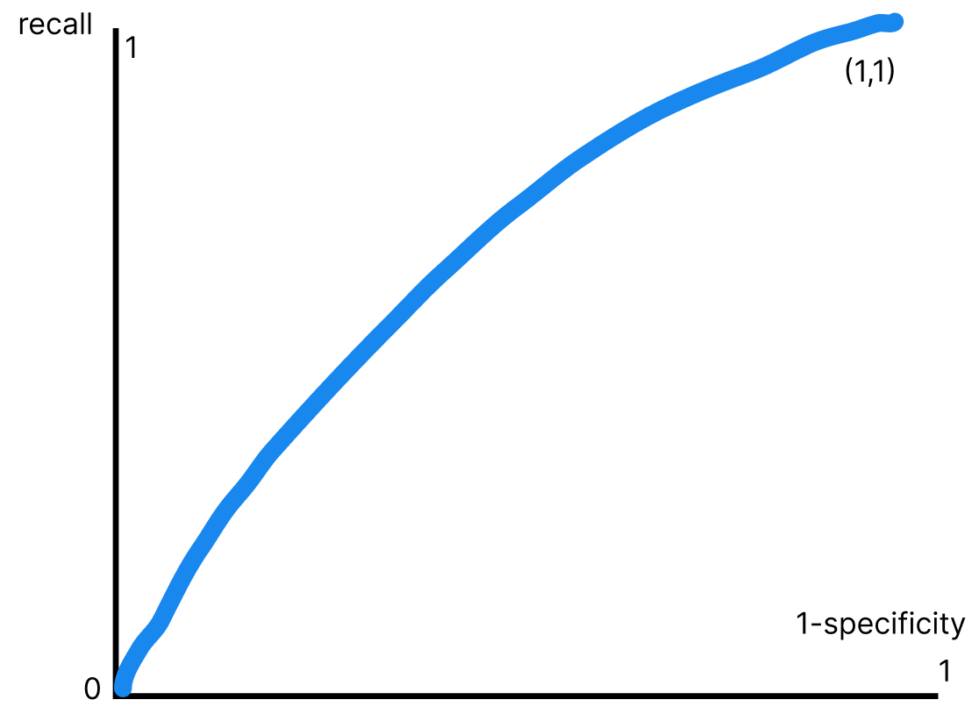
AUC(area under the ROC curve)
そして、上のROC曲線とx軸の間の面積がAUCと呼ばれます。
AUCは結論として、1に近ければ近いほど良いです。
なぜかといえば下図の通り、完全な予測が仮にできている場合にはROC曲線は(0,0)と(1,0)を結んだ直線(縦軸に一致)になります。
この時のAUCは1.0*1.0=1.0となるからです。
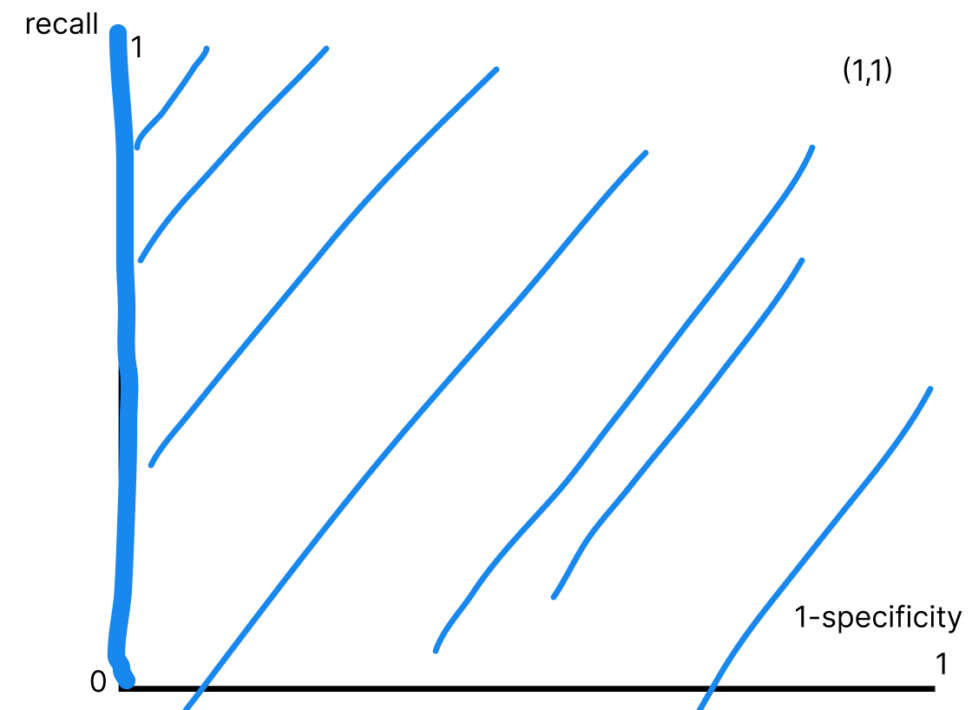
完全な予測ができている場合、常に偽陽性率は0です。
当然ランダムな予測の場合は、ROC曲線は45度線になりますのでAUCは0.5です。
CODE
では実際にAUCを算出してみましょう。
乳がんデータを使います。
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
import numpy as np
import pandas as pd
data_breast_cancer = load_breast_cancer()
# Pandasによるデータの表示
df_target = pd.DataFrame(data_breast_cancer["target"], columns=["target"])
df_data = pd.DataFrame(data_breast_cancer["data"], columns=data_breast_cancer["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
y = df["target"]
X = df.loc[:, "mean radius":]
# 訓練データとテストデータに分ける
X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.5, random_state=0)データの読み込みとデータの確認をします。
| target | mean radius | mean texture | mean perimeter | mean area | mean smoothness | mean compactness | mean concavity | mean concave points | mean symmetry | … | worst radius | worst texture | worst perimeter | worst area | worst smoothness | worst compactness | worst concavity | worst concave points | worst symmetry | worst fractal dimension | |
| target | 1.000000 | -0.730029 | -0.415185 | -0.742636 | -0.708984 | -0.358560 | -0.596534 | -0.696360 | -0.776614 | -0.330499 | … | -0.776454 | -0.456903 | -0.782914 | -0.733825 | -0.421465 | -0.590998 | -0.659610 | -0.793566 | -0.416294 | -0.323872 |
| mean radius | -0.730029 | 1.000000 | 0.323782 | 0.997855 | 0.987357 | 0.170581 | 0.506124 | 0.676764 | 0.822529 | 0.147741 | … | 0.969539 | 0.297008 | 0.965137 | 0.941082 | 0.119616 | 0.413463 | 0.526911 | 0.744214 | 0.163953 | 0.007066 |
| mean texture | -0.415185 | 0.323782 | 1.000000 | 0.329533 | 0.321086 | -0.023389 | 0.236702 | 0.302418 | 0.293464 | 0.071401 | … | 0.352573 | 0.912045 | 0.358040 | 0.343546 | 0.077503 | 0.277830 | 0.301025 | 0.295316 | 0.105008 | 0.119205 |
| mean perimeter | -0.742636 | 0.997855 | 0.329533 | 1.000000 | 0.986507 | 0.207278 | 0.556936 | 0.716136 | 0.850977 | 0.183027 | … | 0.969476 | 0.303038 | 0.970387 | 0.941550 | 0.150549 | 0.455774 | 0.563879 | 0.771241 | 0.189115 | 0.051019 |
| mean area | -0.708984 | 0.987357 | 0.321086 | 0.986507 | 1.000000 | 0.177028 | 0.498502 | 0.685983 | 0.823269 | 0.151293 | … | 0.962746 | 0.287489 | 0.959120 | 0.959213 | 0.123523 | 0.390410 | 0.512606 | 0.722017 | 0.143570 | 0.003738 |
教師データとテストデータに分けます。
# ランダムフォレストによる予測確率の取得
from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier(max_depth=7, min_samples_leaf=1, n_estimators=100, n_jobs=-1, random_state=42)
rfc.fit(X_train, y_train)
# 予測確率を取得
y_pred = rfc.predict_proba(X_valid)[:,1]今回は、ランダムフォレストで予測をしてみます。
決定木系のアルゴリズムを勉強したい方は、以下の記事をご覧ください。
【XGB】交差検証法を使った勾配ブースティング決定木の実装|python
パラメータは適当に設定していますが、本来はチューニングの必要な部分です。
次は、ROC曲線を作図してみます。
# 偽陽性率と真陽性率の算出
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
fpr, tpr, thresholds = roc_curve(y_valid, y_pred)
# AUCの算出
auc = auc(fpr, tpr)
# ROC曲線の描画
plt.plot(fpr, tpr, color='red', label='ROC curve (area = %.3f)' % auc)
plt.plot([0, 1], [0, 1], color='black', linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('Receiver operating characteristic')
plt.legend(loc="best")必要なメソッドはsklearnに大体入っていますのでimportしておきましょう。
roc_curve()に入れる引数としては、予測データと評価データです。
fpr(false positive rate):偽陽性率
tpr(true positive rate):真陽性率。recallです。
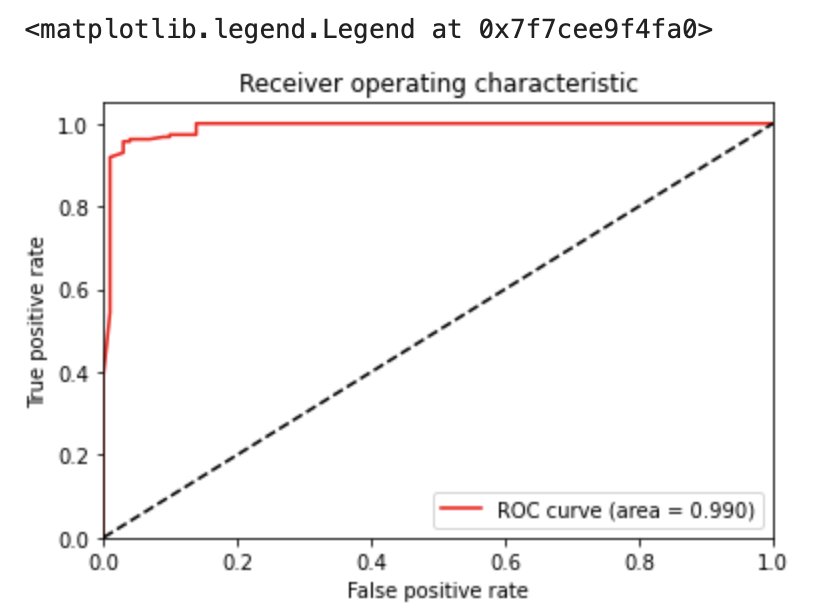
上のようなROC曲線が引けました。
AUC(area)は0.990であることから、ランダムと比べると、かなり高い性能を有したモデルであると確認できます。
混同行列の作成、ROC曲線の形状比較、そしてprecision、recall、F1-score、AUCの大小比較は、モデル選択をする際の基礎的な根拠となります。
ただし、あくまでもそれは選択候補のモデル間に、相対的な順番を与えるものに過ぎませんから、モデルを活用したときに得られるであろうビジネス成果との関係を理解することなく、単なる数値追求だけとなることは避けるよう留意しましょう。
青の統計学は、東京大学を卒業後、事業会社でデータサイエンティストとして勤務する筆者が運営する、AI・データサイエンスの総合学習メディアです。 自身の大学時代の経験から、教科書だと分かりにくかった事項を克服でき、かつ実務で活かせる知識を楽しく学べるように、インタラクティブ学習ツール「DS Playground」を開発しており、大学での講義の材料としても利用されています。Xフォロワー1万人を突破!


