【共変量の調整】傾向スコア・マッチングによる因果推論 | python

こんにちは、青の統計学です。

今回は傾向スコアをご紹介します。

因果推論でよく出てくる考え方ですので、しっかり習得しましょう。

なぜ「そのまま比較」してはいけないのか

例えば、「自社のInstagramに接触したユーザーは、接触しなかったユーザーよりも購入額が高い」というデータがあったとします。

だめですよね。

なぜなら、インスタに接触したユーザー（介入群）と、接触しなかったユーザー（対照群）の間には、元々違いがある可能性が高いからです。例えば、元々購買意欲の高いユーザーや、特定のデモグラフィックを持つユーザーが、より積極的に自社のインスタを見たり、表示される場所に多く滞在したりするかもしれません。

このような、介入群と対照群を分ける原因となり、かつ結果にも影響を与える要因を「交絡因子」と呼びます。交絡因子によって生じる、介入の真の効果ではない「見かけ上の差」のことを「バイアス」と言います。

ようは、比較する対象が異なってしまい、選択バイアスが生まれてしまっているわけです。

当然ですが、私たちが知りたいのは、もし同じユーザーが広告に接触した場合と接触しなかった場合で、購入額にどれだけの差が出るかという、理想的な比較ですよね。

では、どう真実に近づくか。

それが今回紹介する、観察研究データから可能な限りバイアスを取り除き、因果効果を推定するための手法の一つ、「傾向スコアマッチング」です。

傾向スコアの数学的背景：確率で「似ている」を定義する

傾向スコアマッチングを理解するための鍵は、傾向スコアという概念です。

傾向スコアとは何か

傾向スコアとは、群間比較研究において、介入を受けたグループと受けなかったグループの間のバイアスを補正するために用いられるスコアです。

観察研究において介入効果を推定する際に、治療群と比較群を類似にするために用いられます。

先ほどの例を考えてみましょう。

傾向スコア ${e(X)}$ は、ある個人 $i$ が、特定の介入（この例ではInstagram広告接触）を受ける確率を、その個人の持つ背景情報（共変量、ここでは $X$）に基づいて示したものです。

$$e(X) = P(Z=1 | X)$$

• $Z$ は介入変数で、$Z=1$ が介入群（広告接触）、$Z=0$ が対照群（インスタ非接触）
• $X$ は共変量（年齢、性別、過去の購買履歴、アプリ利用時間など）のベクトルです。
• $P(Z=1 | X)$ は、$X$ という背景を持つ人が介入を受ける条件付き確率です。

つまり、共変量Xで条件づけているので、「傾向スコアが同じであれば、その人たちは背景情報 $X$ の分布が同じである」と見なせる、というわけです。

傾向スコアの推定と次元の削減

傾向スコアを推定するために、まず、共変量 $X$ を説明変数とし、介入 $Z$ を目的変数とするロジスティック回帰分析（よく使われます）を行います。

$$\log \left( \frac{P(Z=1 | X)}{1 – P(Z=1 | X)} \right) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots$$

このモデルから得られる予測確率 $P(Z=1 | X)$ が、個々のユーザーの傾向スコアとなります。

しかし、傾向スコア $e(X)$ は、$X$ の情報を集約したたった一つのスカラー値（確率）です。ロジスティック回帰によって、介入を受ける確率という一次元の指標に、高次元の $X$ の情報を凝縮しているのです。

この次元削減のおかげで、「傾向スコアが近いユーザー同士」をマッチングさせることで、「背景情報 $X$ が似ているユーザー同士」を比較するという、理想的な比較に近づくことができるのです。

統計的因果推論の基礎

傾向スコアの概念は、統計的因果推論における枠組みの一つである「ルービンの因果モデル」に根ざしています。

このあたりの記事でも解説しています。

ルービンの因果モデル

ルービンの因果モデルでは、各個人 $i$ について、介入を受けた場合の潜在的な結果 $Y_i(1)$ と、介入を受けなかった場合の潜在的な結果 $Y_i(0)$ の両方が存在すると考えます。

今回の例だと、インスタに接触した、が介入になります。

• 介入群の実際の結果: $Y_i = Y_i(1)$ （$Z_i=1$ の場合）
• 対照群の実際の結果: $Y_i = Y_i(0)$ （$Z_i=0$ の場合）

で、知りたい個人レベルの因果効果は $Y_i(1) – Y_i(0)$ ですが、現実には $Y_i(1)$ か $Y_i(0)$ のどちらか一方しか観測できません。

今回取り上げたようなSNS接触だと少し話は違いますがで、健康状態や年齢の共変量は事前にある程度揃えたあとで実験しろというのが真っ当な意見です。

ただ、割り付けが完全にランダムにできない時や、既にあるデータからインクリメンタルなアウトカムを出さねばならない時に「処置の有無以外の条件を被験者で一緒にしたいよね」というのが傾向スコアのモチベーションであると理解してもらえると嬉しいです。

数学的背景｜条件付き独立について

傾向スコアを使うと、ランダム化に近いことができるのね、と理解いただきましたが、数学的はどう整理されているのでしょうか。

傾向スコアが因果推論において機能するための数学的な前提は、「強く無視できる割当」という仮定です。これは、共変量 $X$ を条件付けたとき、介入の割当 $Z$ が潜在結果 $Y(0), Y(1)$ と独立である、というものです。

$$\{Y(1), Y(0)\} \perp Z \mid X$$

この仮定が成立すれば、傾向スコア $e(X)$ を条件付けた場合でも、同じように独立性が成立することが、証明されています。

$$\{Y(1), Y(0)\} \perp Z \mid e(X)$$

つまり、傾向スコアを一致させて比較することで、観察データをランダム化比較試験（RCT）に近い状態に「補正」できるのです。

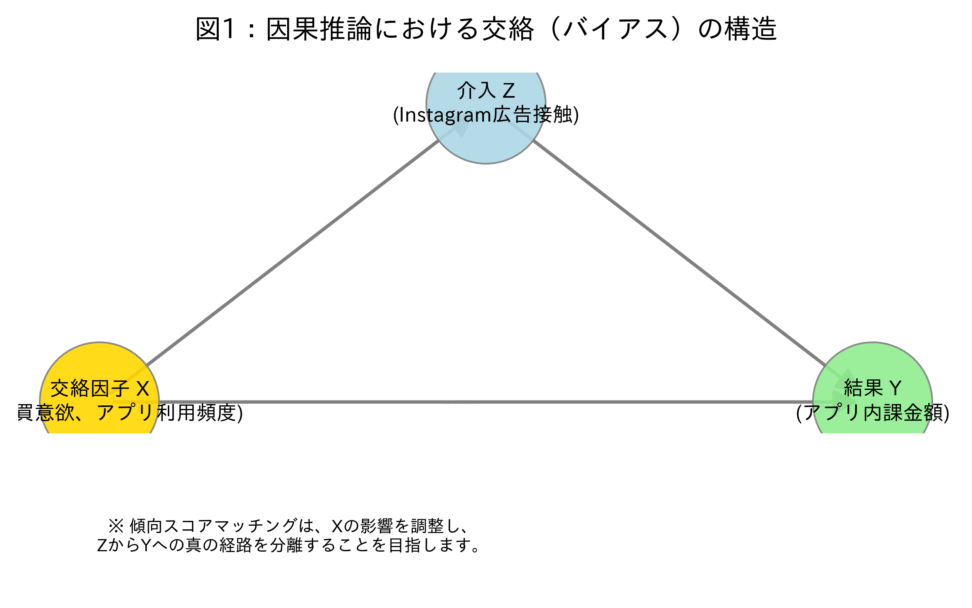
バイアス（交絡）の構造を視覚的に理解しましょう。

交絡因子 $X$ が介入 $Z$ と結果 $Y$ の両方に影響を与えることで、本来の因果関係 $Z \to Y$ の推定を歪めてしまいます。

共通サポート

さて、ここまで見てきたので実践的な手順を確認しましょう。

• 共変量 $X$ の選定と傾向スコアの推定
  • バイアスを生み出す交絡因子を特定し、ロジスティック回帰で傾向スコア $e(X)$ を算出します。
• 共通サポートの確認
  • 介入群と対照群の傾向スコアの分布を比較し、両群がオーバーラップしている領域（共通サポートといいます。）を確認します。

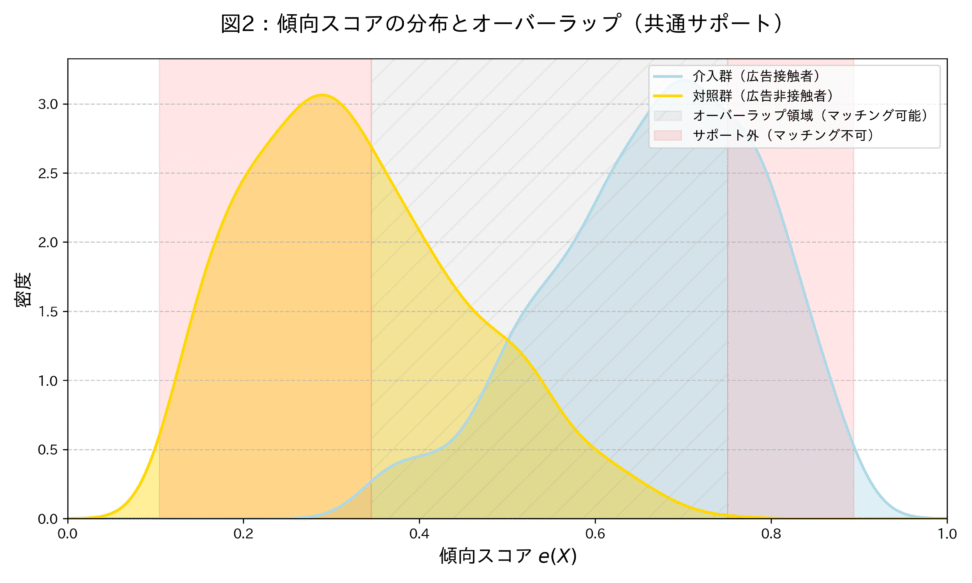
図を見ると、介入群と対照群の傾向スコアの分布には偏りがありました。

特に、傾向スコアが極端に高い（介入を受ける確率が高い）介入群のユーザーや、極端に低い（介入を受けない確率が高い）対照群のユーザーは、比較対象となる「似た者」がもう一方の群に存在しないため、マッチングから除外されますね。

• マッチングの実施
  • 共通サポート内の介入群の各ユーザーについて、**傾向スコアが最も近い**対照群のユーザーをペアとして見つけます（例：1対1最近傍マッチング）。
• バランスの確認
  • マッチング後の介入群と対照群の間で、共変量 $X$ の分布が本当に一致しているか（共変量のバランスが取れているか）を統計的に確認します。
• 効果の推定
  • マッチングによって作られた「似た者同士」のペア間で、課金額の差を計算し、その平均を求めます。

これが「平均介入効果（Average Treatment Effect on the Treated, ATT）」の推定値となります。

補足｜マッチング以外の傾向スコア利用法

手法名	概要	目的
層化	傾向スコアの区間（例：0-0.2, 0.2-0.4, …）でデータを層に分け、各層内で介入群と対照群の結果を比較し、平均を算出する。	傾向スコアの分布を均一化し、層内でのバイアスを低減
IPW	傾向スコアの逆数で各観測値を重み付けし、介入群と対照群の共変量分布を擬似的に一致させる。	介入群と対照群のサンプルサイズが大きく異なる場合に有効
共変量で使う	傾向スコアを共変量の一つとして回帰モデルに投入し、結果を調整	モデルの安定性を高め、残存バイアスをさらに低減する。

補足｜ノンパラメトリック手法

傾向スコアは、ノンパラメトリック手法と言われます。

ノンパラメトリック手法は、パラメトリック手法と違い、目的変数の確率分布が分からなくても良いです。

正しいモデルをわかっていれば、共分散分析は有効です。

しかし、「モデルがわからない」かつ「共変量を置いて、線形関係を仮定したときに明らかに望ましくない」場合にノンパラメトリック手法を使います。　

線形性の過程が必要な共分散分析について知りたい方は、【交絡を解決!?】共分散分析(ANCOVA)とは一体何なのか。をご覧ください。

ランダムな割り付け(ランダム比較化実験など)ができればいいのですが、例えばマーケティングのABテスト(新しいモーダルを見せるor見せない)だと、半数には見せないので毀損が生じる可能性があります。

こうしたABテストなどを実施できない時には、介入以外による影響のバイアスを否定できず、介入効果を過大もしくは過小に評価してしまう恐れがあります。

こんな時に傾向スコアを使うと便利というわけです。

傾向スコアによる解析は準実験と呼ばれます。

準実験とは、処置の無作為な割り付けがない観察研修でも割り付けや比較対象の集団についてなんらかの統制を行うことで無作為化実験を真似するデザインであり、社会科学系でよく使われることが多いです。