【カイ2乗検定】独立性検定と適合度検定についてわかりやすく解説

こんにちは、青の統計学です。

今回は、統計検定2級でも登場する独立性の検定と適合度検定について解説します。

計算自体は理解してしまうと楽なので、ぜひマスターしてくださいね。

合わせて、カイ二乗分布についても知識を深められるように記載していきます。

カイ二乗分布の数学的背景

今回テーマにする検定の背後には、カイ二乗分布という確率分布の存在があります。

ここから理解していきましょう。

より分布を理解したい方はこちらがおすすめです

カイ二乗分布とは何か

カイ二乗（χ²）分布は、統計学において基本的な確率分布の一つです。

この分布は、独立した標準正規分布に従う確率変数の二乗和の分布として定義されます。より形式的に表現すると、$Z_1, Z_2, \ldots, Z_k$が互いに独立で標準正規分布$N(0,1)$に従う確率変数であるとき、その二乗和$X = Z_1^2 + Z_2^2 + \ldots + Z_k^2$はカイ二乗分布に従います。

$$f(x; k) = \frac{1}{2^{k/2}\Gamma(k/2)}x^{k/2-1}e^{-x/2} \quad \text{for } x > 0$$

ここで、$k$は「自由度」と呼ばれるパラメータで、$\Gamma$はガンマ関数です。

自由度$k$は、二乗和を構成する標準正規分布に従う独立な確率変数の数を表します。

分布の形は、こんな感じになっています。

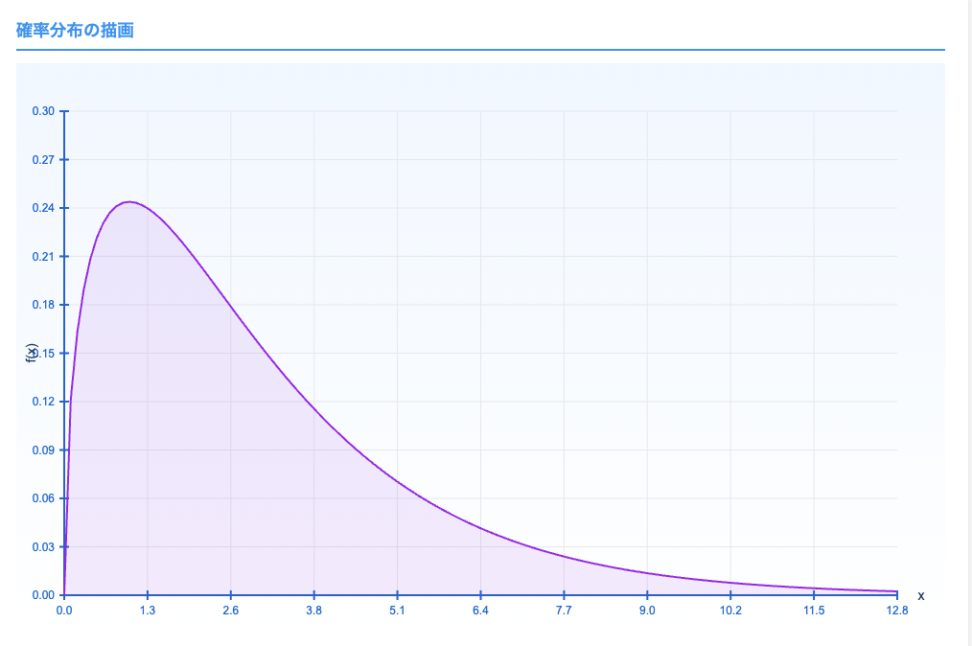
パラメーターを動かして視覚的に理解したい方は、確率分布可視化ツールをご覧ください（PC推奨です）

カイ二乗分布の特性

カイ二乗分布には、以下のような特性があります

1. 期待値と分散
   • 自由度$k$のカイ二乗分布の期待値（平均）は$k$、分散は$2k$です。つまり、自由度が大きくなるほど、分布の中心は右に移動し、ばらつきも大きくなります。
2. 加法性
   • 互いに独立なカイ二乗分布に従う確率変数の和も、カイ二乗分布に従います。具体的には、$X_1 \sim \chi^2(k_1)$と$X_2 \sim \chi^2(k_2)$が独立であれば、$X_1 + X_2 \sim \chi^2(k_1 + k_2)$となります。
3. 非負性
   • カイ二乗分布は非負の値のみをとります（$x \geq 0$）。これは、二乗和として定義されているため当然ですね
4. 正規分布との関係
   • 標準正規分布の二乗は自由度1のカイ二乗分布に従います。また、自由度が十分大きい場合、$\sqrt{2\chi^2(k)} – \sqrt{2k-1}$は近似的に標準正規分布に従います。

２の特性は正規分布や幾何分布、ポアソン分布にもありますね。

自由度の概念とその意味

これに限らずですが、自由度とは一体なんなのでしょうか。

カイ二乗分布において、自由度$k$は単なるパラメータではなく、統計的意味を持っています。

自由度が増加するにつれて、カイ二乗分布の形状は変化します。

自由度が小さい場合（例：$k=1, 2, 3$）、分布は原点付近で高い確率密度を持ち、右に長い裾を引く非対称な形状になります。

逆に、自由度が大きくなるにつれて（例：$k \geq 30$）、分布は次第に対称形に近づき、正規分布に近似していきます。

カイ二乗分布の導出（やや複雑）

カイ二乗分布の導出過程を理解することで、この分布がなぜ統計的検定に適しているのかが明らかになります。

先ほどのセクションでも語りましたが、ここでは、標準正規分布からカイ二乗分布がどのように導かれるかを見ていきましょう。

まず、標準正規分布$N(0,1)$に従う確率変数$Z$の確率密度関数は次のように表されます

$$f_Z(z) = \frac{1}{\sqrt{2\pi}}e^{-z^2/2}$$

ここで、$Z^2$という新しい確率変数を考えましょう。

変数変換の公式を用いると、$Z^2$の確率密度関数$f_{Z^2}(x)$は次のようになります

$$f_{Z^2}(x) = \frac{1}{\sqrt{2\pi}}\frac{1}{2\sqrt{x}}e^{-x/2} \quad \text{for } x > 0$$

これは自由度1のカイ二乗分布の確率密度関数です。

次に、$k$個の独立な標準正規分布に従う確率変数$Z_1, Z_2, \ldots, Z_k$の二乗和$X = Z_1^2 + Z_2^2 + \ldots + Z_k^2$を考えます。

確率変数の和の分布は、各確率変数の分布の畳み込み積分で表されます。

独立性の仮定により、この計算は特性関数（モーメント母関数）を用いると簡単になります。

標準正規分布の特性関数は$\phi_Z(t) = e^{t^2/2}$であり、$Z^2$の特性関数は$\phi_{Z^2}(t) = (1-2t)^{-1/2}$となります。

（↑この辺は統計検定準1級でよく出るので、もはや覚えておきたい。）

$k$個の独立な$Z_i^2$の和の特性関数は、各特性関数の積になるので…

$$\phi_X(t) = \prod_{i=1}^{k} \phi_{Z_i^2}(t) = (1-2t)^{-k/2}$$

これを逆変換すると、自由度$k$のカイ二乗分布の確率密度関数が得られます

$$f(x; k) = \frac{1}{2^{k/2}\Gamma(k/2)}x^{k/2-1}e^{-x/2} \quad \text{for } x > 0$$

この導出過程から、カイ二乗分布が標準正規分布の二乗和として自然に現れることがわかります。

他の確率分布との関連性

カイ二乗分布は、他の確率分布とも関連しています。

さてさて、カイ二乗分布の数学的背景を理解したところで、次節では具体的な検定手法である「適合度検定」について詳しく見ていきましょう。

適合度検定

基本的な考え方

適合度検定（Goodness of Fit Test）は、観測されたデータが特定の理論的分布や期待される分布に「適合」しているかどうかを統計的に評価する手法です。

適合度検定の基本的な考え方はシンプルです。

もし観測データが理論的分布に従うならば、各カテゴリの観測度数と期待度数の差は小さいはずですよね。

逆に、その差が大きければ、データは理論的分布に従っていないと考えられます。

カイ二乗適合度検定では、この「差の大きさ」を定量的に評価するために、カイ二乗統計量を用います。

帰無仮説と対立仮説の設定

適合度検定では、以下のように仮説を設定します

• 帰無仮説（H₀）: 観測データは特定の理論的分布に従う
  • つまり、観測度数と期待度数の差は偶然によるものである
• 対立仮説（H₁）: 観測データは特定の理論的分布に従わない
  • つまり、観測度数と期待度数の差は偶然では説明できない

この仮説設定は、統計的検定の基本的なアプローチですよね。

ここから復習したい方はこちらをどうぞ。

帰無仮説は「差がない」という主張であり、データから十分な証拠が得られない限り、この仮説を棄却しません。

検定統計量の計算方法

カイ二乗適合度検定では、検定統計量として以下のカイ二乗値を計算します：

$$\chi^2 = \sum_{i=1}^{k} \frac{(O_i – E_i)^2}{E_i}$$

• $O_i$ は $i$ 番目のカテゴリの観測度数
• $E_i$ は $i$ 番目のカテゴリの期待度数
• $k$ はカテゴリの総数

この統計量は、観測度数と期待度数の差の二乗を期待度数で割った値の総和です。

差が大きいほど、また期待度数に対する差の割合が大きいほど、カイ二乗値は大きくなります。

期待度数は教科書によっては、理論値とかとも言いますね。

自由度の決定方法

適合度検定における自由度は、カテゴリ数から推定したパラメータ数を引いた値として計算されます：

$$df = k – m – 1$$

• $k$ はカテゴリの総数
• $m$ は推定したパラメータの数

例えば、単純に「特定の理論的分布に従うか」を検定する場合で、パラメータを推定していない場合は $m = 0$ となり、自由度は $k – 1$ です。

これは、$k$ 個のカテゴリの度数の合計が固定されているため、実際に自由に変動できるのは $k – 1$ 個だけであることを反映しています。

p値の解釈と意思決定

計算されたカイ二乗値と自由度から、p値を求めることができます。p値は、「帰無仮説が真であると仮定したとき、観測されたデータと同じかそれ以上に極端なデータが得られる確率」を表します。

p値が小さいほど、帰無仮説（データが理論的分布に従うという仮説）と観測データの間の不一致が大きいことを示します。一般的には、p値が有意水準（通常は0.05または0.01）よりも小さい場合、帰無仮説を棄却します。

ただし、p値の解釈には注意が必要です。

p値が小さいからといって、効果の大きさや実質的な重要性を直接示すわけではありません。

また、p値が大きい場合も、帰無仮説が「証明された」わけではなく、単に「棄却するための十分な証拠がない」ということを意味します。

適合度検定の具体的な手順

さて、適合度検定の具体的な手順をまとめると、以下のようになります。

1. 仮説の設定：帰無仮説（H₀：データは特定の分布に従う）と対立仮説（H₁：データは特定の分布に従わない）を設定します。
2. 期待度数の計算：理論的分布に基づいて、各カテゴリの期待度数を計算します。
3. カイ二乗統計量の計算：観測度数と期待度数を用いて、カイ二乗統計量を計算します。
4. 自由度の決定：カテゴリ数と推定したパラメータ数から自由度を決定します。
5. p値の計算：カイ二乗統計量と自由度から、p値を計算します。
6. 結論の導出：p値と有意水準を比較し、帰無仮説を棄却するかどうかを決定します。

独立性検定

基本的な考え方

独立性検定（Test of Independence）は、二つのカテゴリカル変数間に関連性（依存関係）があるかどうかを統計的に評価する手法です。例えば、「性別と職業選択に関連性があるか」「教育レベルと政治的見解に関連性があるか」といった問いに答えるために使用されます。

つまり、クロス集計表（分割表）の各セルの観測度数は、行と列の周辺度数から計算される期待度数に近いはずですよね。

もし観測度数と期待度数の間に大きな差があれば、それは二つの変数間に何らかの関連性が存在することを示唆します。

分割表（クロス集計表）の構造

独立性検定では、データは通常、行と列の二次元の分割表（クロス集計表）として表されます。

例えば、行が性別（男性、女性）、列が職業カテゴリ（技術職、営業職、管理職など）を表す表を考えてみましょう。

一般的な $r \times c$ の分割表は以下のように表されます

xx	カテゴリ1	カテゴリ2	…	カテゴリc	行合計
カテゴリ1	$O_{11}$	$O_{12}$	…	$O_{1c}$	$R_1$
カテゴリ2	$O_{21}$	$O_{22}$	…	$O_{2c}$	$R_2$
…	…	…	…	…	…
カテゴリr	$O_{r1}$	$O_{r2}$	…	$O_{rc}$	$R_r$
列合計	$C_1$	$C_2$	…	$C_c$	$N$

• $O_{ij}$ は $i$ 行 $j$ 列のセルの観測度数
• $R_i$ は $i$ 行の合計（行周辺度数）
• $C_j$ は $j$ 列の合計（列周辺度数）
• $N$ は総度数（全観測値の合計）

期待度数の計算方法

先ほども扱いましたが、ここでも期待度数の求め方をおさらいです。

概念としては変わらないです。

独立性検定では、二つの変数が独立であるという帰無仮説の下で、各セルの期待度数を計算します。二つの変数が独立であれば、セル $(i,j)$ の期待度数 $E_{ij}$ は以下のように計算されます

$$E_{ij} = \frac{R_i \times C_j}{N}$$

つまり、行周辺度数と列周辺度数の積を総度数で割った値です。

例えば、1000人の調査で、500人が男性（$R_1 = 500$）、300人が技術職（$C_1 = 300$）であれば、男性で技術職の期待度数は $E_{11} = (500 \times 300) / 1000 = 150$ となりますよね。

検定統計量の計算と解釈

独立性検定でも、適合度検定と同様にカイ二乗統計量を用います

$$\chi^2 = \sum_{i=1}^{r} \sum_{j=1}^{c} \frac{(O_{ij} – E_{ij})^2}{E_{ij}}$$

この統計量は、全てのセルにおける観測度数と期待度数の差の二乗を期待度数で割った値の総和です。

二つの変数が独立であれば（帰無仮説が真であれば）、この統計量は自由度 $(r-1)(c-1)$ のカイ二乗分布に近似的に従います。

カイ二乗値が大きいほど、観測度数と期待度数の差が大きいことを示し、二つの変数間に関連性がある可能性が高くなります。

自由度の決定方法

独立性検定における自由度は、$(r-1)(c-1)$ として計算されます。ここで、$r$ は行の数、$c$ は列の数です。

この自由度の計算は、分割表の制約条件から導かれます。$r$ 行 $c$ 列の表には合計 $r \times c$ 個のセルがありますが、行と列の周辺度数が固定されているため、実際に自由に変動できるセルの数は $(r-1)(c-1)$ 個だけです。

例えば、$2 \times 3$ の分割表（2行3列）の場合、自由度は $(2-1)(3-1) = 1 \times 2 = 2$ となります。

独立性検定の具体的な手順

独立性検定の具体的な手順をまとめると、以下のようになります：

1. 仮説の設定：帰無仮説（H₀：二つの変数は独立している）と対立仮説（H₁：二つの変数は独立していない）を設定します。
2. 分割表の作成：データをクロス集計表（分割表）として整理します。
3. 期待度数の計算：各セルの期待度数を、行周辺度数と列周辺度数から計算します。
4. カイ二乗統計量の計算：観測度数と期待度数を用いて、カイ二乗統計量を計算します。
5. 自由度の決定：行数と列数から自由度 $(r-1)(c-1)$ を決定します。
6. p値の計算：カイ二乗統計量と自由度から、p値を計算します。
7. 結論の導出：p値と有意水準を比較し、帰無仮説を棄却するかどうかを決定します。

この手順により、二つのカテゴリカル変数間の関連性を客観的に評価することができます。

簡単にまとめると..

両検定の根底にある考え方は、「観測値と期待値の差が偶然によるものか否か」を評価するというものですね。

カイ二乗統計量は、この差を標準化して合計することで、全体としての不一致の度合いを定量化します。

数学的には、両検定とも以下の形式のカイ二乗統計量を用います

$$\chi^2 = \sum \frac{(観測値 – 期待値)^2}{期待値}$$

この統計量は、帰無仮説が真であれば近似的にカイ二乗分布に従います。

独立性検定の実践例：マーケティングデータの分析

次に、独立性検定の実践例として、マーケティングデータの分析を見ていきましょう。

ある企業が新製品のマーケティングキャンペーンを実施し、異なる年齢層の顧客の反応を調査したとします。

問題設定

ある企業が新製品を発売し、異なる年齢層の顧客に対して購入意向を調査しました。以下のデータが得られました：

年齢層	購入意向あり	購入意向なし	合計
18-30歳	120	80	200
31-45歳	150	50	200
46-60歳	100	100	200
61歳以上	80	120	200
合計	450	350	800

この調査結果から、購入意向と年齢層の間に関連性があるかどうかを検証したいと思います。

解析手順

1. 仮説の設定

• 帰無仮説（H₀）：購入意向と年齢層は独立している（関連性がない）
• 対立仮説（H₁）：購入意向と年齢層は独立していない（関連性がある）

1. 期待度数の計算
   帰無仮説の下での各セルの期待度数を計算します： 例えば、18-30歳で購入意向ありのセルの期待度数は：
   $$E_{11} = \frac{200 \times 450}{800} = 112.5$$ 同様に、全てのセルの期待度数を計算します： 年齢層 購入意向あり 購入意向なし 18-30歳 112.5 87.5 31-45歳 112.5 87.5 46-60歳 112.5 87.5 61歳以上 112.5 87.5
2. カイ二乗統計量の計算
   $$\chi^2 = \sum_{i=1}^{4} \sum_{j=1}^{2} \frac{(O_{ij} – E_{ij})^2}{E_{ij}}$$ $$\chi^2 = 0.5 + 0.64 + 12.5 + 16.07 + 1.39 + 1.79 + 9.39 + 12.07 = 54.35$$
3. 自由度の決定
   行数は4、列数は2なので、自由度は $(4-1)(2-1) = 3 \times 1 = 3$ です。
4. p値の計算
   自由度3のカイ二乗分布において、統計量54.35に対応するp値は非常に小さく（p < 0.001）、実質的に0と見なせます。
5. 結論の導出
   p値は一般的な有意水準（0.05）よりも遥かに小さいため、帰無仮説を強く棄却します。つまり、購入意向と年齢層の間には統計的に有意な関連性があると結論づけられます。

この結果から、購入意向と年齢層の間には強い関連性があることが確認できました。

具体的には、31-45歳の層では購入意向が高く、61歳以上の層では購入意向が低い傾向があります。