【python】尤度比検定で統計モデルの比較をしよう|統計的仮説検定
こんにちは、青の統計学です。
今回は、汎用性抜群な尤度比検定について解説いたします。
Rで解説したものコンテンツは以下になります。
尤度比検定(likelihood ratio test)
尤度比検定(Likelihood Ratio Test)は、統計学において、2つの確率分布のうち、あるデータが得られる確率がより高い方を選ぶための手法です。
尤度比検定は、2つの確率分布のパラメータが未知の場合に使用されます。
尤度比検定の主要な思想は、2つの確率分布があり、それらのうち1つが真であると仮定し、それを検証するために、それらが生成したデータの質を比較することです。それぞれの確率分布に対して、データが得られる確率(尤度)を計算し、それらを比較します。
尤度比が最も高い確率分布が真とみなされます。
尤度とは(likelihood)
尤度(likelihood)は、統計学においてデータがある確率モデルに従って生成されたと仮定した(確率モデルのパラメーターが与えられた)ときの、
そのデータが観測される確率を表します。
例えば、平均値 μ、標準偏差 σが与えられた正規分布に従ってデータが生成されたと仮定した場合、尤度は、次の式で計算されます
$$L(μ,σ)= \frac{1}{σ \sqrt{2π}^2}exp(- \frac{(x-μ)^2}{2σ^2})$$
ここで、xは観測されたデータ、nは観測されたデータの数です。
もっと具体に言えば、「コインを100回投げて、50回表になる時の確率」を尤度L(p)、コインを一回投げて表になる確率のことをパラメーターpと当てはめています。
余談ですが、最尤法とはこの尤度が最大になるためのパラメータを推定量として求めようという手法です。
これは、観測された事象は、「起きやすい確率が最大のものが起きている」という考えから派生しています。
尤度比について
さて尤度比検定は、特に統計モデルの比較に使用されます。
例えば、2つの異なる統計モデルがあり、それらのうちどちらがより適しているかを決定するために、それらが生成したデータの質を比較することができます。
この時に、尤度比を使います。
尤度比検定では、以下のような2つの比較モデルが考えられます。
- 帰無仮説(H0)として、モデル1が有効
- 対立仮説(H1)として、モデル2が有効
尤度比は以下のような式です。
$$L=\frac{L(H1)}{L(H0)}>c$$
この形で、棄却域が与えられます。
単一ニ仮説の場合は、尤度比検定は一様最強力検定となります。
→ネイマン・ピアソンの定理
尤度比は、観測データが対立仮説のモデルに従う確率を帰無仮説のモデルに従う確率で割った値です。
尤度比が大きければ、対立仮説のモデルが適合している可能性が高いことを示します。
尤度比検定における検定統計量について
尤度比検定は、ある統計的帰無仮説が正しいかどうかを判定するために使用され、帰無仮説が棄却される場合に対立仮説が採択されます。
一般には尤度比検定統計量の帰無仮説のもとでの確率分布は分かりません。
しかし嬉しいのが、サンプル数が十分大きい時には、尤度比検定統計量の対数に2をかけたものがカイ2乗分布に従う性質にあります。
$$D=2L=2(logL_{H1}^*-logL_{H0}^*)$$
対数なので、割り算は引き算になります。
これは、【良いモデルとは】AIC(赤池情報量基準)について。で登場した「逸脱度」です
$$2log \frac{対立仮説の最大尤度}{帰無仮説の最大尤度}$$
$$2logL〜χ_{n}^{p}$$
そしてこの加工された検定統計量は、自由度nのカイ二乗分布に従います。
自由度は帰無仮説の制約数によります。
つまり最尤推定するパラメータの数ですね。
カイ二乗分布(Chi-squared distribution)
カイ二乗分布とは、多変量正規分布の中心極限定理に基づいて、確率変数Z_nが標準正規分布に従うとき、各確率変数の平方和が従う確率分布のことです。
尤度比検定の漸近理論で使います。
$$Z_{1},…,Z_{n}〜N(0,1)$$
$$Z_{1}^2+…+Z_{n}^2〜χ^2(d)$$
また、カイ二乗分布は以下のような確率密度関数に従います。
ここで、xは自由度nのカイ二乗分布に従う乱数、nは自由度です。
$$f(x;n)=\frac{1}{2^{\frac{n}{2}}}× x^{\frac{n}{2}-1}× exp(- \frac{x}{2})$$
補足ですが、カイ二乗分布はガンマ分布の特別な形としても理解することができます。
ガンマ分布は形状パラメータ\(\frac{k}{2}\)と尺度パラメータ\(2\)のガンマ分布がカイ二乗分布に一致します。この関係から、カイ二乗分布の確率密度関数は以下のように表されます。
$$f(x;k)=\frac{1}{2^{\frac{k}{2}Γ(\frac{k}{2})}}x^{\frac{k}{2}-1}e^{-\frac{x}{2}}$$
ここで \(x≥0\) であり、\(Γ\)はガンマ関数です。
CODE|python
今回は、乳がんデータセットを使って、特徴量を削減したモデルとそのままのモデルで、どちらが良いモデルなのかを調べたいと思います。
どの特徴量を削除するのかに関しては、ランダムフォレストで特徴量重要度が低い特徴量を削除します。
少し長いコードになりますが、多くのエッセンスがあると思うので、参考になれば嬉しいです。
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn import metrics
import numpy as np
from scipy.stats import chi2
from sklearn.ensemble import RandomForestClassifier
import matplotlib.pyplot as plt
# データセットのロード
data_breast_cancer = load_breast_cancer()
# Pandasによるデータの表示
df_target = pd.DataFrame(data_breast_cancer["target"], columns=["target"])
df_data = pd.DataFrame(data_breast_cancer["data"], columns=data_breast_cancer["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
y = df["target"]
X = df.loc[:, "mean radius":]
# 教師データとテストデータに分割する
X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.2, random_state=42)
seed=42
#グリッドサーチでハイパーパラメーターのチューニングを行う。
scores = {}
for max_depth in range(3, 10, 1):
for min_samples_leaf in range(2, 10, 1):
model = RandomForestClassifier(max_depth=max_depth,
min_samples_leaf=min_samples_leaf,
n_estimators=100,
random_state=seed
)
model.fit(X_train, y_train)
scores[(max_depth, min_samples_leaf)] = model.score(X_valid, y_valid)
# 検証結果をscoresに格納
scores = pd.Series(scores)
# 表示
print('ベストスコア:{:.2f}'.format(scores.max()))
print('その時のパラメータ(max_depth, min_samples_leaf):{}'.format(scores.idxmax()))
array_bst = np.array(scores.idxmax())
max_depth = array_bst[0]
min_samples_leaf = array_bst[1]
model_bst = RandomForestClassifier(max_depth=max_depth,
min_samples_leaf=min_samples_leaf,
n_estimators=100,
random_state=seed
)
model_bst.fit(X_train, y_train)
# 過学習確認
pred_rfc_class = model_bst.predict(X_valid)
pred_rfc_proba = model_bst.predict_proba(X_valid)[:, 1]
# 過学習確認
print("教師データ",model_bst.score(X_train, y_train))
print("テストスコア",model_bst.score(X_valid, y_valid))
#feature_importanceで特徴量重要度を算出する
feature = pd.DataFrame()
feature["columns"] = X.columns
feature["score"] = model_bst.feature_importances_
feature = feature.sort_values(by='score', ascending=False)
plt.figure(figsize=(50,40))
plt.plot(feature["columns"], feature["score"])
plt.title("feature_importance")
plt.show()グリッドサーチを使って、ハイパーパラメーターのチューニングをしています。
さて、ランダムフォレストで特徴量重要度を算出すると、以下のようなグラフができました。
今回は、思い切って重要度が高い10個の特徴量のみを算出することにします。
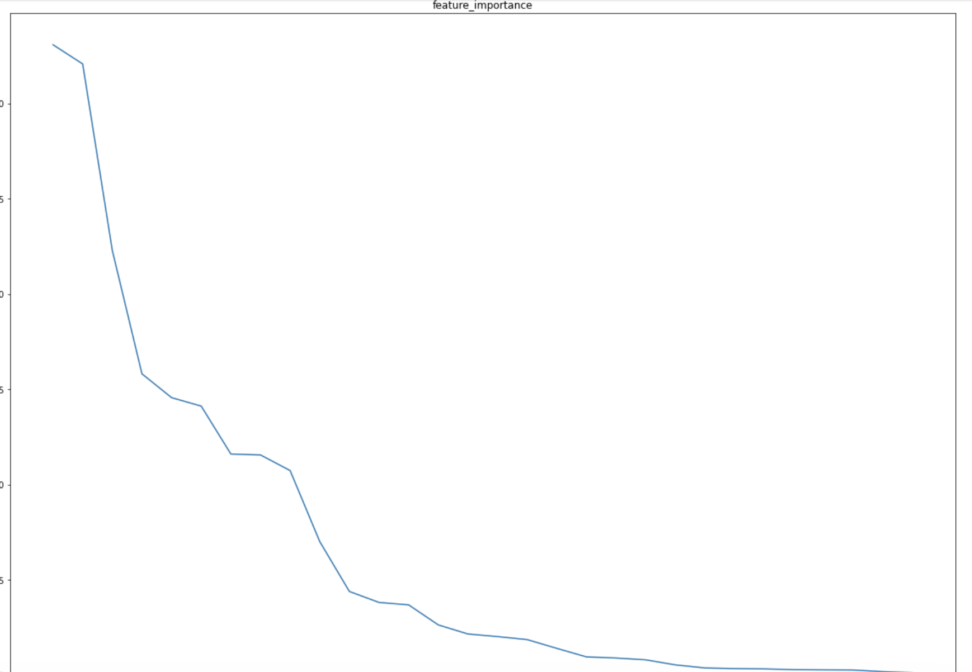
ランダムフォレストをはじめとした、決定木系のアルゴリズムは以下のコンテンツで学習できます。
【ランダムフォレスト】ブートストラップ法を決定木に応用|python
【XGB】GridSearchを使いつつ特徴量重要度を知りたいッ‥!|python
【XGB】交差検証法を使った勾配ブースティング決定木の実装|python
# データセットの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# ロジスティック回帰による学習
clf_full = RandomForestClassifier()
clf_full.fit(X_train, y_train)
# 特徴量を削減していないモデルで尤度を算出
y_prob_full = clf_full.predict_proba(X_test)
# 特徴量を削減したモデルをロジスティック回帰で作る
X_train_reduced = X_train[["worst area","worst concave points","mean concave points","worst radius",
"worst perimeter","mean concavity","mean area","mean perimeter","mean radius","worst concavity"]]
X_test_reduced = X_test[["worst area","worst concave points","mean concave points","worst radius",
"worst perimeter","mean concavity","mean area","mean perimeter","mean radius","worst concavity"]]
clf_reduced = RandomForestClassifier()
clf_reduced.fit(X_train_reduced, y_train)
y_prob_reduced = clf_reduced.predict_proba(X_test_reduced)
# 対数尤度の計算
ll_full = metrics.log_loss(y_test, y_prob_full, labels=[0,1])
ll_reduced = metrics.log_loss(y_test, y_prob_reduced, labels=[0,1])
# 尤度比検定統計量の算出
lrt = 2 * (ll_reduced - ll_full)
# p値の算出
p_value = 1 - chi2.cdf(lrt, 1)
print("Likelihood Ratio Test statistic: ", lrt)
print("P-value: ", p_value)Likelihood Ratio Test statistic: -0.0023589593679397836
尤度比を見る限り、対立仮説(特徴量を削減したモデル)の尤度の方が小さいようです。
尤度比検定は、異なる統計モデル間の比較に用いられることが多いですが、単一のモデルに対しても使用することができます。
単一のモデルに対して使用する場合、帰無仮説は、そのモデルが有効であること、対立仮説は、そのモデルが有効でないことを示します。
統計的仮説検定については、以下のコンテンツをご覧ください。
【仮説検定】p値をゼロから解説(第一種の過誤,第二種の過誤,検出力)
補足|尤度比の使い道、KL divergenceについて
尤度比の使い方として、KL divergenceをご紹介します。
二つの確率分布\(q(\textbf{x})\)と\(p(\textbf{x})\)がどれくらい異なるかを測るための非対称な距離尺度です。
これは情報理論の中で一般的に使われ、特に確率分布や統計モデル間の相違度を測定するのに便利です。
$$KL[q(\textbf{x})|p(\textbf{x})]=\int q(\textbf{x})log\frac{q(\textbf{x})}{p(\textbf{x})}d\textbf{x}$$
上のように尤度比の対数の期待値をとっていることがわかります。
KLダイバージェンスがゼロ、つまり最小値になるのはPとQが同じ分布である場合のみです。
ただ、二つの確率分布を並列に扱っているわけではなく、一つの確率分布(ここでは\(p(x)\))を真の確率分布と仮定した場合に、別の確率分布を(ここでは\(q(x)\))用いて情報を符号化するときの“情報損失”を測定します。
KLダイバージェンスは尤度比の対数を一種の”期待値”として捉えることができます。
つまり、Pが真の分布であるとき、それに基づいて生成される各データ点において、Pに基づく尤度の対数とQに基づく尤度の対数との差(これが尤度比の対数に相当します)の”Pによる期待値”がKLダイバージェンスとなります。
そのため、KLダイバージェンスは統計的推論における尤度比の概念を、全確率分布に対する尺度として一般化したものと考えることができます。
詳しくは以下のコンテンツをご覧ください。
【AICで使う】KL divergence(カルバック-ライブラー情報量)をわかりやすく解説|python

