【説明変数の相関】多重共線性を解説します。
重回帰分析を勉強していると、最小二乗法の仮定の一つに「多重共線性がないこと」と見たことがあると思います。
今回は、多重共線性の内容と、対処法を2つ解説いたします。
多重共線性の論文に関しては、以下で解説しています。
【論文解説】多重共線性は回帰分析にどのような影響を与えるのか
多重共線性(Multicollinearity)
結論から言うと、「説明変数に相関がありすぎる」ことです。
具体例を見ていきましょう。
年収がどのような要素によって決定されていくのか重回帰分析で調べたいと思います。 調査対象は30歳の日本人100人です。 「個人の年収Yi」を目的変数におき、説明変数に「教育年数X1」と「父親の年収X2」をおきます。
$$Y_{i}=β_{0}+β_{1}X_{1i}+β_{2}X_{2i}+u_{i}$$
\(β_{0}\)は定数項で、\(u_{i}\)は誤差項です。
重回帰分析は、各説明変数がどのくらいYに貢献しているのか調べることです。
多重共線性があり、説明変数同士が相関し合っていると、目的変数の値が不安定になります。
「不安定」と言うのは、残差が大きくなるということです。
予測値と実際のデータの乖離が大きくなると、モデル自体の信頼性は低いです。
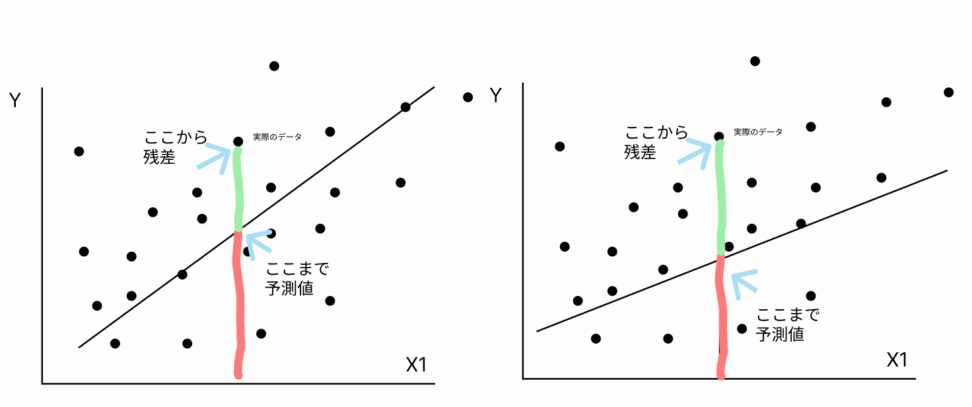
今回のモデルでいうと、父親の年収が高いほど、その子供の教育年数は多くなるのはなんとなく想像がつきそうです。
つまり、説明変数の設定の仕方があまり良くないということです。
今回の統計モデルの目的が、「説明変数の係数を知りたい」なので多重共線性があるとモデルの信憑性がなくて駄目です。
ただ、統計モデルの目的が、「目的変数の予測を行いたい」である場合は問題ありません。
多重共線性の基準
説明変数同士がどのくらい相関していれば、「多重共線性がある」と言えるのでしょうか。
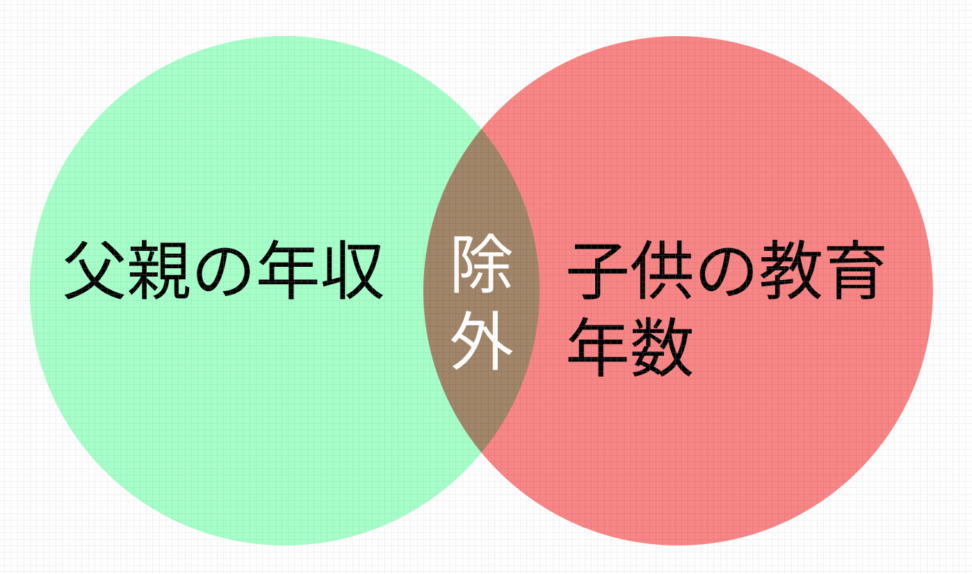
教育年数のうち、父親の年収による部分をモデルから除外することで、ちゃんとした重回帰分析はできます。
実際は、R等の統計解析ソフトでは、多重共線性の影響は除外された形で推定値は出力されています。
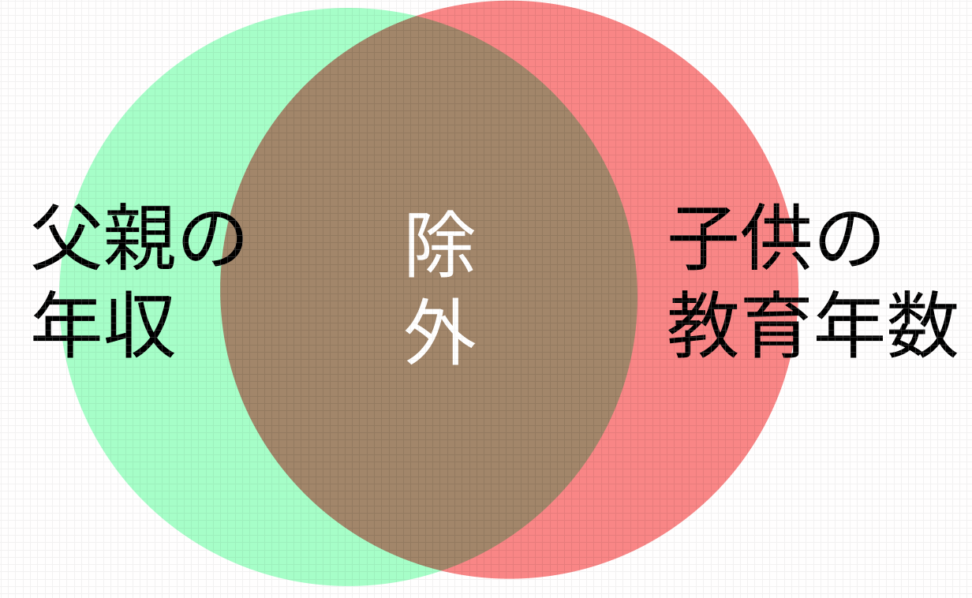
ただし上のように、重なっている部分が大きいと統計ソフトが除外する部分が多く、データのごく一部だけで係数を推定することになり微妙です。
VIF(Variance Inflation Factor)
では、定量的な多重共線性の指標として、VIFをご紹介します。
$$VIF = \frac{1}{1-R_{j}^2}$$
rは説明変数X1とX2の相関係数を表します。
正の相関であろうが、負の相関であろうが、相関が大きい場合にVIFの値は大きくなります。
10より大きいと多重共線性があると言われています。
ただ、この多重共線性の判定基準であるVIFの妥当性には疑問がついています。(だからと言って計量経済学で多重共線性の問題を考えないということではありません)
VIF|CODE
ここではVIFを計算するコードを載せています。
各カラムの1行下(1行目ですね)に特徴量のVIFを載せるプログラムです。
乳がんデータという特徴量が多めのデータセットを使っているためか、かなりVIFが大きいです。
# Import libraries
import pandas as pd
from sklearn.datasets import load_breast_cancer
import numpy as np
from statsmodels.stats.outliers_influence import variance_inflation_factor
data_breast_cancer = load_breast_cancer()
df_target = pd.DataFrame(data_breast_cancer["target"], columns=["target"])
df_data = pd.DataFrame(data_breast_cancer["data"], columns=data_breast_cancer["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
# Get column names
columns = df.columns
# Create VIF dataframe
vif_data = pd.DataFrame()
# Calculate VIF for each column
for i in range(0,len(columns)):
vif = variance_inflation_factor(df[columns],i)
vif_data.loc[0,columns[i]] = vif
# View VIF dataframe
vif_data| target | mean radius | mean texture | mean perimeter | mean area | mean smoothness | mean compactness | mean concavity | mean concave points | mean symmetry | … | worst radius | worst texture | worst perimeter | worst area | worst smoothness | worst compactness | worst concavity | worst concave points | worst symmetry | worst fractal dimension | |
| 0 | 10.884558 | 63955.019898 | 251.093672 | 58213.349861 | 1320.282793 | 393.418392 | 200.983909 | 158.033586 | 155.053368 | 184.712502 | … | 9993.710616 | 343.419477 | 4498.196282 | 1165.384639 | 375.640625 | 132.918704 | 86.754853 | 148.773818 | 219.621611 | 427.782984 |
線形代数による定義
説明変数間に強い相関がある場合、データ行列Xの列ベクトルが線形従属(一方が他方の線形結合で表される)に近くなります。
これにより、行列\(X^T X\)はランクが不足し、特異行列に近づくことがあります。
定量的には\(rank(A)<n\)で多重共線性があると言われます。
$$\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ k a_{11} & k a_{12} \end{bmatrix}$$
特異行列は逆行列が存在しないため、連立方程式が一意的な解を持たない(不能)ことを意味します。
説明変数間に高い相関がある場合(多重共線性)、データ行列Xがほぼシンギュラー(特異行列となり、行列式が0になる)になることがあります。
→逆行列が存在しても、数値的な不安定性が生じ、計算が収束せず、解析解が不正確になることがあります。
これが多重共線性における基本的な悪影響を指します。
では逆行列がないとなぜ解析的にパラメータを求められないかという疑問にお答えします。
まず線形回帰の目的関数(損失関数)は以下のようになっております。
$$J(w) = ||Xβ – y||^2$$
パラメータβで偏微分して一階条件を適用すると、
$$J(w) = ||Xβ – y||^2$$
$$∇J(w) = 0$$
となります。これを書き換えると
$$X^T X β = X^T y$$
$$β = (X^T X)^{-1} X^T y$$
最適パラメータを求めるにはデータ行列Xの逆行列が必要ということですね。
さて、多重共線性が強く特異行列になってしまったとすると、
$$X^{-1}=X × \frac{1}{|X|} \tilde{X}$$
行列式|X|が0なら、逆行列は存在しませんね!
つまり、解析解で使用する逆行列を求められないということになります。
代替案として最急勾配降下法のような方法で近似的に最適なパラメータを求めることが必要です。
ダミー変数の罠
以下の例をご覧ください。
今度は年収に与える影響を調べるために、以下のようなダミー変数を与えました。 H:高卒ダミー。高卒なら1、大卒なら0。 C:大卒ダミー。高卒なら0、大卒なら1。 母集団は高卒以上の集団であるとし、大卒か高卒かの2通りに必ずわかれるとします。 この時、多重共線性はあるでしょうか?
$$Y_{i}=β_{0}+β_{1}H_{i}+β_{2}C_{i}+u_{i}$$
答え:多重共線性はあります。
母集団には、高卒と大卒しかいませんので、ある個人iに関して以下の関係が必ず成り立ちます。
$$H_{i}+C_{i}=1$$
よって、このような反例が作れるので上の定義に基づき、多重共線性がある言えます。
$$-\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{3}}H_{i}+\frac{1}{\sqrt{3}}C_{i}=0$$
一般的に、
①どれか一つのダミー変数が1の時に他は0をとる
②どれかのダミー変数は必ず1をとる
場合、定数項を含めると多重共線性が発生します。これを、ダミー変数の罠と言います。
この多重共線性は、「定数項かダミー変数2つ」のうち一つを除外すれば解決できます
3通り考えられますね。例えば以下のモデルです。
$$Y_{i}=β_{0}+β_{1}H_{i}+u_{i}$$
よく考えれば、ある個人が大卒の時、Cは1でHは必ず0でした。これは、説明変数が負の相関を持っていると言えます。
多重共線性の解決方法としては
①説明変数を消す
②主成分回帰
③回帰係数の重みを小さくする
④共線性のある説明変数を組み合わせて一つの説明変数とする
ですが、今回は①だったと言うわけです。
説明変数を一つ消したのは、
「相関しているのなら、消しても影響はモデルに残るから消してしまおう」という意味です。
重回帰分析で多重共線性を解決する手法の一つに「正則化項を加える」がありますが、以下のコンテンツでは正則化について扱っています。
【python】Ridge(リッジ)回帰で多重共線性を解決する話
単回帰分析よりも重回帰分析の方が、基本的に説明力が高くなります。そのため、説明変数をたくさん入れたモデルの方が良いと感じる人も多いでしょう。
しかし、説明変数を増やせば増やすほど、モデルが複雑になることで実用性が下がり、加えて多重共線性のリスクは高まります。
説明変数を加える際は気をつけましょう。
回帰分析については、【機械学習】単回帰分析をpythonで実装してみましょうをご覧ください。

