SARIMAモデルについてわかりやすく解説｜定常時系列解析
SARIMAモデル
SARIMA（Seasonal AutoRegressive Integrated Moving Average）モデルは、時系列データの予測に用いられるモデルです。時系列データに存在する、トレンド、季節性、自己相関といった特徴を捉えることで、より精度の高い予測を可能にします。
各要素の意味
- AR（AutoRegressive）： 自己回帰。過去の自身の値が現在の値に影響を与えることを表します。
- I（Integrated）： データの定常性を確保するために、差分をとる操作です。
- MA（Moving Average）： 移動平均。過去の誤差項が現在の値に影響を与えることを表します。
- Seasonal: 季節的なパターンを考慮します。
他の時系列解析については、こちらのコンテンツがオススメです。
モデル
SARIMAモデルは、一般的に以下の式で表されます。
$$ {y_t = c + \phi_1 y_{t-1} + … + \phi_p y_{t-p} + \theta_1 \epsilon_{t-1} + … + \theta_q \epsilon_{t-q} +\\ \Phi_1 y_{t-s} + … + \Phi_P y_{t-sP} + \Theta_1 \epsilon_{t-s} + … + \Theta_Q \epsilon_{t-sQ} + \epsilon_t }$$
- ${y_t}$: 時点tにおける観測値
- ${c}$: 定数項
- ${ϕ_i}$: AR項の係数
- ${θ_j}$: MA項の係数
- ${Φ_i}$: 季節的なAR項の係数
- ${Θ_j}$: 季節的なMA項の係数
- ${ϵ_t}$: 白色雑音、ホワイトノイズですね。
- ${p}$: AR項の次数
- ${q}$: MA項の次数
- ${P}$: 季節的なAR項の次数
- ${Q}$: 季節的なMA項の次数
- ${s}$: 季節の長さ
各要素の役割
- AR項: 過去の値との線形な関係を表します。例えば、株価が昨日、一昨日と上昇していれば、今日も上昇する可能性が高いというような関係性が考えられます。
- I項: データにトレンドや季節性がある場合、定常性を持たせるために差分をとります。差分をとることで、データの平均や分散が一定になるように調整します。
- MA項: 過去の誤差項との線形な関係を表します。誤差項とは、モデルで説明できない部分、つまりノイズのようなものです。
- 季節項: 季節的なパターンを表します。例えば、小売業の売上は季節によって大きく変動することがあります。
ちょっと単純な例で具体例を見てみましょう。
具体例｜施策の効果の推定
競合施策による自社KPIへの影響値を確認したいです。
経営陣は、同業のキャンペーン施策が自社のキャンペーン施策に影響を与え、それが結果的にKPIに影響するのではないかということを気にしています。
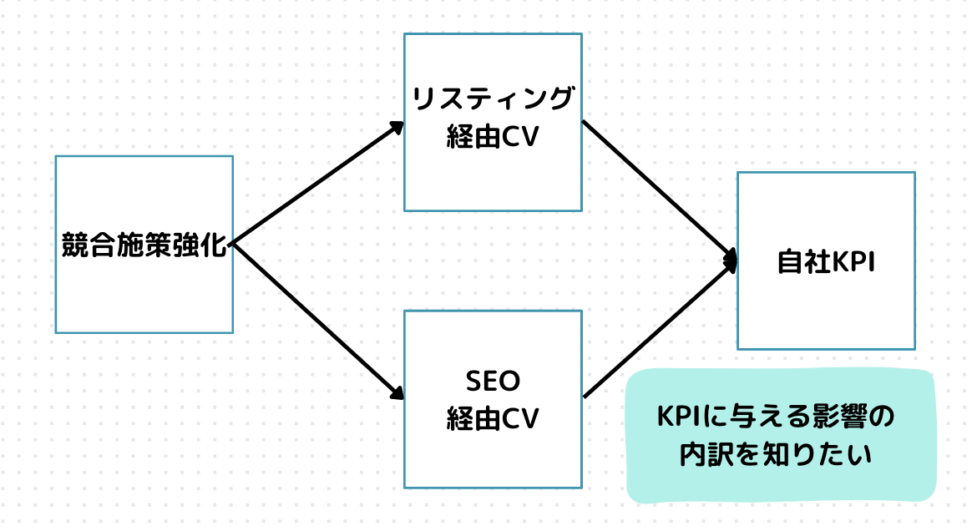
基本的に施策によるROIや増分効果や増分コストなどを見る場合、属性がほぼ同じのコントロール群と介入群を分けて、同じ\(t\)期のアウトカムの差分を見れば、平均処置効果がわかります。
ただ、今回は同業の施策効果なのでそのようなデータはないです。
多分影響するとは思いますが、どれだけ影響するかによって、「自社のキャンペーンを強化すべきか」「強化すべきならどのように強化するのが最適か」などが変わってきます。
SEO経由のコンバージョンには大した影響はないが、SNS経由のコンバージョンには大きな影響がある、などどのチャネル経由でKPIに影響するのかも気になりますよね。
| time | KPI | SEO経由CV | Lis経由CV | 自社施策-競合施策の金額差分 | 競合施策ダミー |
| 23/10 | 7000 | 4000 | 2000 | 0 | 0 |
| 23/11 | 5000 | 2000 | 1500 | -4000 | 1 |
| … | … | … | … | …. | … |
自社も同業も恒常的にキャンペーンを実施しており、今回は同業がキャンペーン金額を強化して自社キャンペーンが負けている状況を考えます。
キャッシュバックキャンペーンやポイント付与キャンペーンなど、世の中にはいろいろなバラマキ施策がありますね。
今回もその一つとして考えてください。
モデルの構築
時系列分析を使って自社と同業の金額差分を外生変数に加え、その回帰係数を求めると言うものです。
KPIには1年周期の季節性がありましたので、以下のようなSARIMAモデルを考えました。
$$(1-φ_1L)Y_t=δ+(1-Φ_1L^{12})ε_t+β_xDiff_{t}$$
上は一般形ではなく、例として、\(SARIMAX(1, 0, 0)(1, 0, 0)[12]\)モデルの数式を表現しています。
このモデルは、非季節性の自己回帰（AR）成分が1次、移動平均（MA）成分が0次、差分（I）成分が0次であり、季節性のAR成分が1次、MA成分が0次、季節性の差分成分が0次であることを意味します。また、周期は12期です。季節性の自己回帰（SAR）成分が1つあることを意味します。
各変数の意味
- \(Y_t\)はt期の目的変数、SEO経由CVとかですね。
- \(L\)はラグ演算子です。後述します。
- \(φ_1\)は非季節性自己回帰(AR)の1次の係数です。
- \(Φ_1\)は季節性自己回帰(SAR)の12期の係数です
- \(δ\)は定数項
- \(ε_t\)はt期の誤差項です。
- \(Diff\)は自社と同業のキャンペーン金額の差分ですね。今回はこの説明変数の特徴量ベクトルを求めたらいいじゃん。私は思いました。
これらを踏まえて、各項の意味を考えてみます。
各項の意味
- ${(1-φ_1L)Y_t}$: 非季節性の自己回帰部分。過去の1期前の値が現在の値に影響を与えることを表します。
- ${δ}$: 定数項。時系列の平均的なレベルを表します。
- ${1-Φ_1L^{12}ε_t}$: 季節性の自己回帰部分。12期前の誤差項が現在の値に影響を与えることを表します。
- ${β_xDiff_{t}}$: 外生変数である同業とのキャンペーン金額の差分が、目的変数に与える影響を表します。
モデルの解釈
- 非季節性: 過去の1期前のSEO経由CVが、現在のSEO経由CVに直接的な影響を与えることを意味します。
- 季節性: 1年周期の季節変動があり、12ヶ月前の誤差項が現在の値に影響を与えることを意味します。
- 外生変数: 同業とのキャンペーン金額の差分が、自社のSEO経由CVに正または負の影響を与える可能性があります。
ラグ演算子(lag operator)について
\(L\)、ラグ演算子（Lag Operator）は、時系列分析において非常に重要な概念で、時系列データの過去の値にアクセスするために使われます。
以下のような形で、過去の時点の値にアクセスすることができます。
$${L^kY_t=Y_{t-k}}$$
- ${L^k}$: ラグ演算子を${k}$回繰り返すことを意味します。
- ${Y_t}$: 時点tにおける変数${Y}$の値です。
- ${Y_{t-k}}$: 時点${t}$から${k}$期前の変数${Y}$の値です。
上のように、${t}$期時点のアウトカムを${t-k}$時点のアウトカムを使って表せます。
これは「ラグ演算子を${k}$回適用した状態」と呼びます。
ラグ演算子を使うと何が嬉しいのか
さて、たとえばARIMAモデルでは、非定常時系列を定常時系列に直すために差分を取りますが、ラグ演算子を使うと表現が簡単です。
つまり、モデルの安定性や因果性に関する理論的な特性を分析しやすくなります。
auto_arimaなどで探索されたパラメータによって形は変わりますが、以下のように表現できます。
$${(1-φ_1L-φ_2L^2-…-φ_pL^p)Y_t=δ+ε_t+移動平均項}$$
モデルのパラメータがデータのラグされた値にどのように影響を及ぼしているかを直感的に理解しやすくなります。
また、モデルの係数が時系列の動的な挙動をどのように捉えているかの解釈が容易になります。
ラグ演算子は統計検定準1級で出ましたね。
ラグ演算子のメリット
時系列モデルの簡潔な表現: 時系列モデルを、ラグ演算子を用いてコンパクトに表現できる
過去のデータとの関係性の可視化: 過去のデータが現在のデータに与える影響を定量的に分析できます。
CODE|python
＊ランダムに生成したデータを使うので、結果は参考にはなりません。
今回使うpmd_auto_arimaは、ARIMAの次数を、機械学習的なのりで、予測精度を最大限に高める次数を自動探索し決めようというライブラリです。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pmdarima import auto_arima
from sklearn.metrics import mean_absolute_error, mean_squared_error
# データの読み込み（月次データを生成）
np.random.seed(0)
dates = pd.date_range('2020-01-01', periods=100, freq='M')
data = np.random.uniform(2000, 10000, 100)
df = pd.DataFrame(data, columns=['SEO_cv'], index=dates)
# 外生変数「diff」を追加（-5000から+5000の範囲のランダムな値）
df['diff'] = np.random.uniform(-5000, 5000, size=len(df))
# auto_arima
model = auto_arima(df['SEO_cv'], X=df[['diff']], seasonal=True, m=12,
trace=True, error_action='ignore', suppress_warnings=True)
print(model.summary())ここではランダムにデータを生成しています。
公式のドキュメントを参照し、外生変数として同業とのキャンペーン金額差分を「diff」としてX=diffとして引数に入れています。
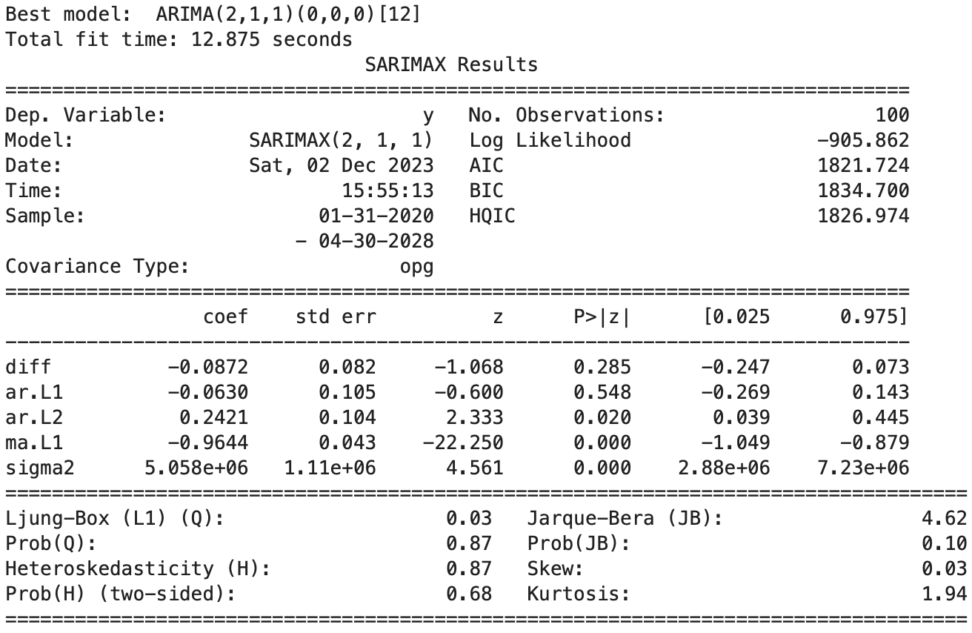
今回diffの回帰係数を見ると、-0,0872でした。
同業のキャンペーン金額が上がった方が、SEO経由CVが上がるという解釈になります。
これは、ランダムなデータですので参考になりませんが、仮説としては同業のキャンペン金額の方が高いと、コンバージョンは落ちます。
ドメイン知識を使って分析結果は解釈していきましょう。
# モデルを使って予測を行う
train = df[:-10] # training data
test = df[-10:] # test data
model.fit(train['SEO_cv'])
forecast = model.predict(n_periods=len(test))
# 実際の値と予測値を比較する
plt.figure(figsize=(10, 6))
plt.plot(train.index, train['SEO_cv'], label='Train Data')
plt.plot(test.index, test['SEO_cv'], label='Test Data', color='gray')
plt.plot(test.index, forecast, label='Forecast', color='red')
plt.title('SEO_cv Forecast vs Actuals')
plt.xlabel('Date')
plt.ylabel('SEO_cv')
plt.legend()
plt.show()
# 評価
mae = mean_absolute_error(test['SEO_cv'], forecast)
mse = mean_squared_error(test['SEO_cv'], forecast)
print(f"Mean Absolute Error: {mae}")
print(f"Mean Squared Error: {mse}")では教師データとテストデータを使って結果を評価するコードを紹介します。
Mean Absolute Error: 2188.6810528495616 Mean Squared Error: 5854630.946243917
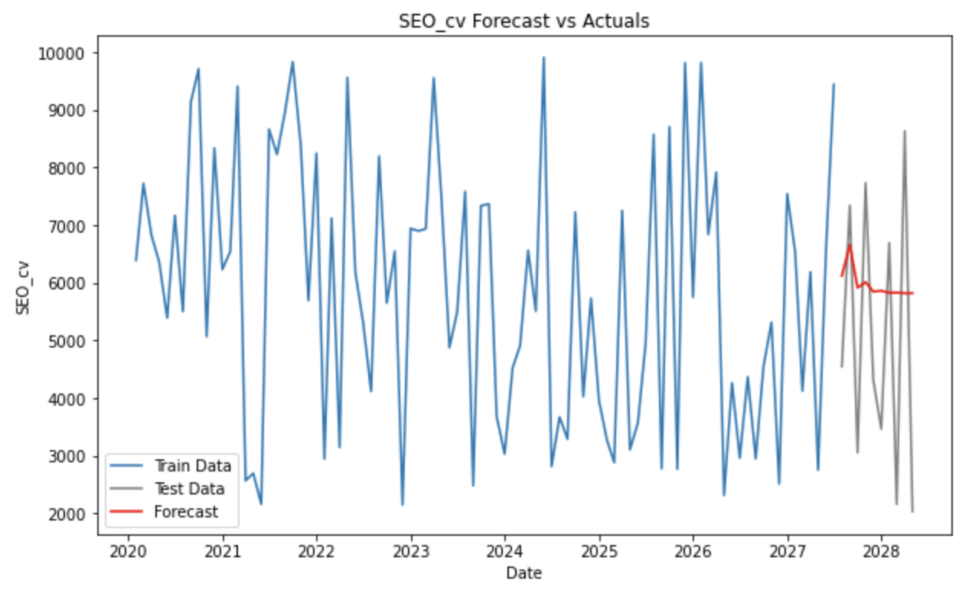
モデルの解釈について考えます。
出力を見ると、auto_arimaによる探索では、ARIMA(2,1,1)(0,0,0)[12]がベストらしいです。
このモデルを数式にしてみましょう。
$$(1-φ_1L-φ_2L^2)\nabla Y_t=δ+θ_1ε_{t-1}+ε_t$$
\(φ\)は自己回帰係数ですね。モデルが過去期間のデータポイントを参照していることを示しています。
\(θ_1\)は移動平均係数ですね。MAの次数が1です。
このモデルでは、季節性成分は考慮されていないため、(0,0,0)[12] の部分はモデルの数式には直接現れません。
季節性周期が12期ということは、データに年次の季節性がある場合に考慮する必要がありますが、このモデルでは季節性の効果は表現されませんでした。
